 |
Число степеней свободы частицы
|
|
|
|
Вопросы коллоквиума
1. Фазовое пространство для идеального газа. Микросостояние и макросостояние. Фазовый ансамбль. Число степеней свободы. Число микросостояний. Плотность микросостояний фазового ансамбля. Теорема Лиувилля.
2. Каноническое распределение. Условие применимости. Статистический интеграл. Свободная энергия. Применение к идеальному газу. Статистический интеграл поступательного движения частицы.
3. Распределение энергии частицы по степеням свободы для гамильтониана со степенными зависимостями. Неустранимая погрешность измерительного прибора с упругой силой.
4. Распределение Максвелла по модулю скорости и по энергии для концентрации частиц. Наиболее вероятные и средние значения.
5. Распределение Больцмана по координатам для концентрации частиц. Формула Больцмана для однородного поля тяжести.
6. Термодинамические потенциалы. Внутренняя энергия. Химический и электрохимический потенциал. Условие равновесия системы. Химический потенциал и статистический интеграл. Зависимости химического потенциала.
КЛАССИЧЕСКАЯ СТАТИСТИЧЕСКАЯ ФИЗИКА
Основные положения
Изучаемая система – идеальный газ частиц, подчиняющихся классической механике.
Микросостояние системы – совокупность координат и импульсов всех частиц, зафиксированных в один момент времени. Отображается точкой X фазового пространства. Возможность тех или иных микросостояний определяет функция распределения 
в фазовом пространстве и статистический интеграл Z – нормировочная постоянная распределения.
Макросостояние системы – состояние газа как единого целого. Описывается термодинамическими величинами – температурой Т, давлением Р, внутренней энергией U, свободной энергией F и др. Термодинамические характеристики являются средними по распределению и получаются на основе Z.
|
|
|
Фазовое пространство системы частиц
Микросостояние системыотображается точкой фазового пространства
,
где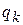 
и 
– обобщенные координаты и импульсы частиц системы. С течением времени точка X движется согласно уравнениям Гамильтона
,
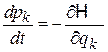. (2.1)
Гамильтониан 
– полная энергия системы, выраженная через координаты и импульсы частиц
.
Для нерелятивистской классической частицы массой m, движущейся вдоль оси k с импульсом 
, кинетическая энергия
.
Для консервативной системы полная энергия сохраняется
,
и все микросостояния находятся на гиперповерхности в фазовом пространстве.
Найдем число измерений фазового пространства.
Число степеней свободы частицы
Число степеней свободы f есть число независимых координат, определяющих положение частицы в пространстве. Изменение координаты означает движение, тогда f – число независимых видов движений.
Атом в трехмерном пространстве имеет координаты (x,y,z) и 
. Изменение координат дает три поступательных движения. Вращательные движения не изменяют координат.
Двухатомная молекула. Два атома дают 6 координат. Если между атомами жесткая связь длиной l, тогда координаты связаны уравнением
.
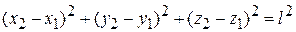Независимы 
координат. Их изменение дает 3 поступательных и 2 вращательных движения. Вращение вокруг оси y не изменяет координаты.
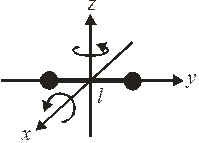
Упругая связь добавляет 2 степени свободы – кинетическую и потенциальную энергию колебаний, тогда для упругой связи 
.
Молекула из N атомов имеет 
координат.
При 
3 степени свободы – поступательные движения,
3 – вращения.
Если связи жесткие, то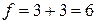 
.
|
|
|
– число связей между атомами.
Если связи упругие, то 
.
Например, для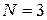 
получаем 
.
«Вымерзание» степеней свободы
Молекула состоит из атомов, атом содержит ядро и электроны в оболочке. Эти структуры обладают внутренними степенями свободы. Обычно энергия связи 
структурных элементов молекулы велика по сравнению с тепловой энергией 
, поэтому внутренние степени свободы не активизируются и не проявляются.
При понижении температуры газа «вымерзают» колебательные движения молекулы, вызванные упругими связями, и для многоатомной молекулы с в трехмерном пространстве 
.
Далее «вымерзают» вращательные движения и .
При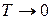 
«вымерзают» поступательные движения, теплоемкость стремится к нулю согласно третьему началу термодинамики, и 
.
|
|
|
