 |
Кинетической и потенциальной энергии частицы
|
|
|
|
при температуре Т
Средняя энергия выражается через статистический интеграл частицы
. (2.19)
Интегрируем по 
, используя метод по частям:
, 
,
, 
,
тогда
.
Свободное слагаемое равно нулю за счет экспоненты. В результате
,
где использовано каноническое распределение
(2.16)
и определение среднего
.
В результате
,
и аналогично
.
Подставляем гамильтониан
,
получаем
,
.
Результаты не зависят от i и j, т. е. теорема о равном распределении тепловой энергии по степеням свободы выполняется. Учитываем
,
,
тогда средние значения потенциальной, кинетической и полной энергий частицы
,
,
. (2.39)
Примеры
1. Нерелятивистская свободная частица
, 
.
Сравниваем с
, (2.38)
в виде
,
находим
, 
,
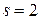. (2.40)
Для классического равновесного газа на каждую поступательную степень свободы частицы приходится тепловая кинетическая энергия 
.
2. Линейный гармонический осциллятор
.
Сравниваем с
, (2.38),
получаем
, 
,
,
,
– на гармоническое колебательное движение приходится тепловая энергия kT.
НЕУСТРАНИМАЯ ПОГРЕШНОСТЬ
ИЗМЕРИТЕЛЬНОГО ПРИБОРА
Макрохарактеристики равновесной системы постоянны только в среднем. Колебания – флуктуации – вызваны хаотическими тепловыми движениями молекул.
Измерительное устройство испытывает тепловые колебания. Невозможно измерить физическую величину с точностью, меньшей амплитуды колебаний указателя прибора.
Оценим неустранимую погрешность прибора на примере весов, используя теорему о распределении энергии по степеням свободы.
|
|
|
Весы на основе упругой силы
Весы – одномерная система. Потенциальная энергия
,
x – отклонение указателя от положения равновесия 
;
– коэффициент жесткости.
Упругая возвращающая сила
.
Равновесие упругой и гравитационной сил
.
Добавление массы 
изменяет показание весов на 
,
тогда
,
где чувствительность
.
Чем меньше коэффициент жесткости, тем выше чувствительность весов.
Средняя потенциальная энергия, связанная с одномерным тепловым хаотическим движением весов, согласно (2.39)
, 
, 
,
.
Флуктуация показаний весов
определяет наименьшую измеряемую массу
– неустранимая погрешность измерения.
Для уменьшения погрешности необходимо уменьшать температуру и увеличивать чувствительность весов.
Последнее требует уменьшениякоэффициента жесткости, который определяет частоту колебаний весов
,
нагруженных массой m. Используем 
, тогда относительная погрешность измерения
.
При w = 10 Гц, Т = 290 К, m = 10–3 г, получаем d m / m» 10–5.
Предельная чувствительность усилителя сигналов
Для колебательного контура
LCR – колебательный контур; У – усилитель.
Тепловое хаотическое движение электронов в резисторе R создает кратковременный ток, конденсатор заряжается, в контуре возникают колебания. Беспорядочные усиленные сигналы поступают на осциллограф.
Найдем флуктуацию напряжения на входе усилителя. Дисперсия напряжения связана с дисперсией заряда на конденсаторе
.
Конденсатор – одномерная система с энергией 
, что соответствует
, , ,
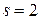тогда средняя тепловая энергия
, 
,
.
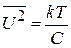Чем меньше электроемкость колебательного контура, тем больше флуктуация напряжения на конденсаторе.
Для колебательного контура ширина частотной полосы
|
|
|
и реактивное сопротивление на резонансной частоте
.
При согласованной нагрузке
,
где 
– входное сопротивление усилителя, тогда
,
,
и флуктуация напряжения
. (П.4.1)
Для приемника с полосой пропускания Dn = 10 кГц, входным сопротивлением R у = 10 кОм, температурой Т = 290 К получаем d U = 1,6 мкВ, что ограничивает предельную чувствительность усилителя.
|
|
|
