 |
Средняя квадратичная скорость
|
|
|
|
РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА–БОЛЬЦМАНА
Дает распределение частиц идеального газа при температуре T во внешнем поле по координатам, скоростям, импульсам и энергии.
Распределение по скоростям без внешнего поля получил Дж. Уотерстон в 1843 г. и Джеймс Максвелл в 1859 г.
Распределение по импульсам и координатам во внешнем поле установил Людвиг Больцман в 1866 г.
Распределение по скоростям, импульсам и энергии без внешнего поля называется распределением Максвелла.
Распределение по координатам во внешнем поле – распределением Больцмана.
Распределение по координатам и импульсам
Для N тождественных частиц идеального газа во внешнем поле при фиксированных температуре и объеме используем каноническое распределение
, 
,
, (2.17)
.
Для частицы трехмерного газа с поступательным движением
,
, 
.
Кинетическая энергия, зависящая от импульса, и потенциальная энергии, зависящая от координат, являются слагаемыми гамильтониана. В каноническом распределении гамильтониан находится в показателе экспоненты. Поэтому распределения по координатам и импульсам являются сомножителями в результирующем распределении
,
,
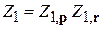– распределение Максвелла, т. е. вероятность обнаружения у частицы импульса в единичном интервале около значения p.
- распределение Больцмана, т. е. вероятность обнаружения у частицы координаты в единичном интервале около значения x.
Распределение Максвелла
Частицы в газе имеют различные скорости, вызванные тепловым движением – от самых малых до самых больших.
Для трехмерного идеального газа без внешнего поля с учетом лишь поступательных движений получим распределения по импульсам, скоростям, энергиям в декартовых и сферических координатах при температуре T.
|
|
|
Распределение по импульсам
В декартовых координатах
,
,
,
каноническое распределение
дает
.
Интегрируем по координатам, учитываем 
, тогда
– вероятность обнаружения частицы с импульсом в интервале 
, где 
.
Распределение по скоростям
Заменяем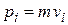 
, 
:
(2.41)
– вероятность обнаружения частицы со скоростями в интервале 
.
Интегрируем (2.41) по 
и 
в пределах (–¥, ¥), используем интеграл Пуассона
, 
,
получаем
, (2.42)
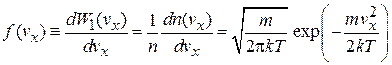(2.42а)
– функция распределения по проекции скорости – относительное число частиц с проекцией скорости в единичном интервале около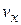 
;
n – концентрация частиц – число частиц в единице объема со всеми скоростями;
– концентрация частиц со скоростями в интервале 
около ;
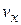– концентрация частиц со скоростями в единичном интервале около .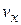
Нормировка
,
,
.
Площадь под кривой – единица;
с ростом Т максимум понижается, график расширяется, увеличивается вероятность обнаружить частицу с большей скоростью;
при 
получаем 
– все частицы останавливаются.
Средняя квадратичная проекция скорости
. (2.42б)
Доказательство:
Подставляем
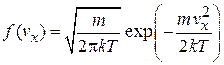, (2.42а)
находим
,
где использовано
,
, , 
.
Распределение в сферических координатах
В (2.41)
|
|
заменяем
,
,
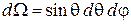получаем
, (2.43)
где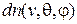 
– концентрация частиц со скоростями от (v, q, j) до (v+dv, q+ d q, j+ d j).
Распределение по модулю скорости
Интегрируем (2.43) по углам, учитываем 
:
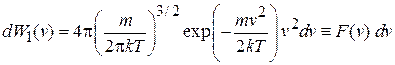(2.44)
– вероятность обнаружения частицы с модулем скорости от v до 
,
(2.44а)
– функция распределения по модулю скорости – относительное число частиц с модулем скорости в единичном интервале около 
;
|
|
|
dn (v) – концентрация частиц с модулем скорости от v до ;
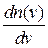– концентрация частиц с модулем скорости в единичном интервале около v.
Условие нормировки
,
площадь под кривой – единица;
с ростом Т максимум понижается, сдвигается вправо и увеличивается вероятность обнаружить частицу с большей скоростью.
Наиболее вероятная скорость
,
.
Из (2.44а)
|
находим
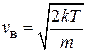(2.45)
Средняя скорость
.
Подставляем
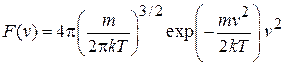, (2.44а)
находим
. (2.46)
Доказательство:
,
,
, , 
.
Средняя квадратичная скорость
.
Подставляем (2.44а)
. (2.47)
Распределение по энергии
Заменяем
, 
, 
,
в распределении по модулю скорости (2.44)
|
получаем
(2.48)
, (2.48а)
– распределение Максвелла по энергии – относительное число частиц с энергией в единичном интервале около 
;
– концентрация частиц с энергией от ε до e + d e;
– концентрация частиц с энергией в единичном интервале около .
Нормировка
.
Площадь под кривой – единица;
с ростом Т максимум понижается, сдвигается вправо и увеличивается вероятность обнаружить частицу с большей энергией.
|
|
|
