 |
Распределение микросостояний по фазовому пространству
|
|
|
|
В каноническом распределении
(2.16)
свободную энергию F выражаем через W-потенциал, используя:
. (2.68)
Получаем
. (2.70)
– вероятность, что система иметь N частиц и находится в элементе объема 
фазового пространства.
Интеграл состояния
Условие нормировки
дает
.
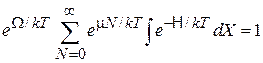Определяем интеграл состояния
, (2.71)
Тогда из нормировки
.(2.72)
Используем статистический интеграл
, (2.17)
из (2.71) получаем связь между статистическими интегралами Z и Z Б
. (2.73)
Для идеального газа из N одинаковых частиц
,
тогда
.
Учитываем
, (2.62б)
получаем
, (2.74)
где 
– среднее число частиц системы.
Большое каноническое распределение
Из
, (2.70)
, (2.72)
получаем
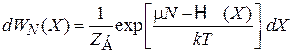. (2.75)
Вероятность наличия N частиц в системе
Интегрируем (2.75) по фазовому пространству:
.
Из
(2.17)
получаем вероятность N частиц в системе
(2.76)
С учетом
(2.73)
Выполняется условие нормировки
.
Термодинамические характеристики системы
Из
, 
, 
, (2.69)
(2.72)
находим
, (2.77)
, (2.78)
– уравнение состояния. (2.79)
Физический смысл (2.78)
С учетом
, (2.73)
, (2.76)
выражение (2.78) сводится к определению среднего числа частиц
.
ПРИМЕР
Вывод формулы Больцмана
Из условия термодинамического равновесия
Используем химический и электрохимический потенциалы идеального газа атомов, совершающих поступательные движения:
, (2.62а)
, (2.59)
,
где 
– потенциальная энергия частицы в точке 
.
При 
определяем 
и получаем
.
Из условия термодинамического равновесия
|
|
|
, (2.60)
находим
,
получаем
и формулу Больцмана
. (П.7.12)
Вопросы коллоквиума
1. Фазовое пространство для идеального газа. Микросостояние и макросостояние. Фазовый ансамбль. Число степеней свободы. Число микросостояний. Плотность микросостояний фазового ансамбля. Теорема Лиувилля.
2. Каноническое распределение. Условие применимости. Статистический интеграл. Свободная энергия. Применение к идеальному газу. Статистический интеграл поступательного движения частицы.
3. Распределение энергии частицы по степеням свободы для гамильтониана со степенными зависимостями. Неустранимая погрешность измерительного прибора с упругой силой.
4. Распределение Максвелла по модулю скорости и по энергии для концентрации частиц. Наиболее вероятные и средние значения.
5. Распределение Больцмана по координатам для концентрации частиц. Формула Больцмана для однородного поля тяжести.
6. Термодинамические потенциалы. Внутренняя энергия. Химический и электрохимический потенциал. Условие равновесия системы. Химический потенциал и статистический интеграл. Зависимости химического потенциала.
СПЕЦГЛАВЫ ФИЗИКИ
Экзамен
1. Биномиальное распределение. Дробовой шум.
2. Статистическое описание системы частиц в фазовом пространстве. Функция распределения. Теорема Лиувилля.
3. Микроканоническое распределение. Энергетическая плотность состояний. Термодинамические величины. Применение к идеальному газу.
4. Каноническое распределение. Статистический интеграл. Термодинамические величины. Применение к идеальному газу.
5. Распределение энергии по степеням свободы. Неустранимая погрешность измерительного прибора. Закон Дюлонга и Пти.
6. Распределение энергии по степеням свободы. Флуктуационная ЭДС в активном сопротивлении.
|
|
|
7. Распределение Максвелла по скорости и по энергии. Формула Ричардсона.
8. Распределение Больцмана. Газ в центрифуге.
9. Распределение Больцмана. Поляризация диэлектрика.
10. Термодинамические характеристики системы с переменным числом частиц. Химический потенциал и его вычисление для идеального газа.
11. Большое каноническое распределение. Выражения для термодинамических характеристик.
12. Распределение Максвелла–Больцмана для частиц по состояниям.
13. Полуклассическая квантовая механика. Квантование одномерных систем. Условия применимости.
|
|
|
