 |
Ориентационная поляризация диэлектрика
|
|
|
|
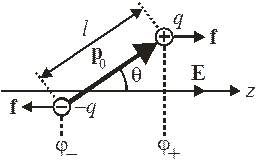
Молекула полярного диэлектрика (например, H2S) имеет электрический дипольный момент с модулем 
. У разных молекул диполи направлены по различным направлениям. Внешнее электрическое поле 
поворачивает диполи и устанавливает их вдоль поля, возникает ориентационная поляризация. Тепловое движение разбрасывает направления диполей. Найдем среднюю проекцию дипольного момента на направление поля, определяющую поляризацию диэлектрика, т. е. дипольный момент единицы объема.
В однородном электрическом поле Е, направленном по оси z, потенциальная энергия диполя
.
Доказательство:
В однородном электрическом поле потенциал точки z
.
Эквипотенциальные поверхности направлены перпендикулярно оси z
.
Для заряда q потенциальная энергия
,
тогда для диполя
,
где
, 
.
Для получения средней проекции дипольного момента используем распределение Больцмана
. (2.55)
Выбираем сферические координаты с осью z, направленной по полю, тогда
.
Потенциальная энергия 
и вероятность не зависят от радиуса. Интегрируем (2.55) по радиусу и получаем
,
где элемент телесного угла
.
Потенциальная энергия и вероятность не зависят от φ. Интегрируем по φ, тогда
,
,
.
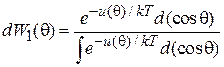Упрощаем выражения вводя
– относительная энергия взаимодействия,
,
.
Получаем
.
Используем
,
находим функцию распределения ориентаций дипольного момента
. (П.6.5)
Средняя проекция дипольного момента
.
Интегрируем по частям
, 
, 
,
,
, (П.6.6)
где L (a) – функция Ланжевена.
В слабом поле
, 
,
,
, ,
,
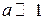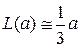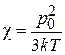– ориентационная поляризуемость,
|
|
|
χ – обратно пропорциональна температуре.
В сильном поле
, ,
, 
,
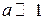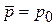
– все диполи ориентированы по полю – насыщение.
Поль Ланжевен разработал статистическую теорию парамагнетизма в 1905 г. и получил результат, аналогичный (П.6.6).
Петер Дебай применил в 1911 г. статистический метод Ланжевена для поляризации диэлектриков и назвал функцию (П.6.6) именем Ланжевена.
В честь Дебая названа внесистемная единица электрического дипольного момента
1 Д (дебай) = 1×10–18 ед. СГС = 3,33564×10–30 Кл×м.
Термодинамические потенциалы
Основные положения
Статистическая величина характеризует микросостояние.
Термодинамическая величина характеризует макросостояние и является средним по микросостояниям фазового ансамбля.
Термодинамический потенциал зависит от состояния системы и не зависит от пути перехода к этому состоянию. Понятие ввел Гиббс в 1874 г.
Рассмотрим систему, состояние которой определяется термодинамическими параметрами 
. Если переход между точками
не зависит от формы пути, то выбираем путь, состоящий из участков, параллельных осям, тогда изменение потенциала 
выражается полным дифференциалом
.
Термодинамические потенциалы имеют по три аргумента и отличаются их выбором:
· внутренняя энергия 
,
· свободная энергия 
,
· химический потенциал 
,
· энтропия 
,
· термодинамический потенциал Гиббса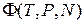 
,
· W-потенциал 
.
Потенциалами не являются:
· работа A,
· теплота Q.
Соотношения между потенциалами, полученные при 
, сохраняются при переменном N.
Условие равновесия системы. Если для рассматриваемого процесса выбрать потенциал, аргументы которого не изменяются в ходе процесса, тогда в равновесном состоянии системы выбранный потенциал минимален.
Химический потенциал
В систему добавляем частицу, в результате изменяется часть термодинамических параметров 
Выбираем термодинамический потенциал, у которого первые два аргумента не меняются при добавлении частицы. Химический потенциал равен изменению термодинамического потенциала при добавлении частицы в систему, если неизменны остальные переменные, от которых зависит потенциал.
|
|
|
При 
получаем
.
Химический потенциал равен изменению внутренней энергии при добавлении одной частицы, если система имеет постоянный объем и не обменивается теплом (d S = 0).
Химический потенциал равен изменению полной энергии системы при приближении частицы к частицам системы. Если частицы взаимно притягиваются, то химический потенциал отрицательный, т. к. сближение частиц уменьшает энергию взаимодействия. Если частицы взаимно отталкиваются, то химический потенциал положительный, т. к. сближение частиц увеличивает энергию взаимодействия.
Химический потенциал находится из условия нормировки на число частиц системы. Если число частиц не сохраняется, то химический потенциал равен нулю.
Электрохимический потенциал 
Характеризует систему во внешнем поле
, (2.59)
m – химический потенциал без поля;
u (r) – энергия частицы в поле.
Далее доказано, что электрохимический потенциал одинаков во всех точках равновесной системы 
, поэтому он характеризует не одну частицу, а систему частиц.
В электростатическом поле
,
j(r) – потенциал точки поля, где находится частица с зарядом q.
Химический потенциал ввел Джозайя Уиллард Гиббс в 1875 г.,
электрохимический потенциал – Эдвард Арманд Гуггенгейм в 1929 г.
Внутренняя энергия 
Является средним по фазовому ансамблю значением полной энергии системы
.
Для обратимого процесса при первое начало термодинамики дает
,
.
С учетом
,
при переменном N получаем
. (2.57)
Используем полный дифференциал
,
находим
, 
, 
. (2.58)
|
|
|
