 |
Наиболее вероятная энергия
|
|
|
|

 .
.
Из (2.48а)

|
получаем
 . (2.49)
. (2.49)
Средняя энергия
 (2.50)
(2.50)
согласуется с теоремой (2.39) о распределении кинетической энергии по степеням свободы. При  получаем
получаем  .
.
Доказательство (2.50):
Используем
 , (2.48а)
, (2.48а)
находим
 ,
,
 ,
,
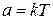 ,
,  ,
,  .
.
Плотность потока частиц  по оси z
по оси z
 – среднее число частиц, проходящих за 1с через единичную площадку, перпендикулярную к оси.
– среднее число частиц, проходящих за 1с через единичную площадку, перпендикулярную к оси.
Движения по x и y не влияют на результат, поэтому считаем эти скорости нулевыми.
Проходящие за 1с частицы с проекцией скорости  заполняют в начальный момент цилиндр с единичным основанием, с образующей вдоль оси z длиной
заполняют в начальный момент цилиндр с единичным основанием, с образующей вдоль оси z длиной  . Концентрация таких частиц
. Концентрация таких частиц  . Через 1с все эти частицы пересекут правое основание цилиндра, их число
. Через 1с все эти частицы пересекут правое основание цилиндра, их число  .
.

Суммируем по всем скоростям с положительной проекцией и получаем
 .
.
Используем (2.42а)
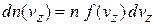 , ,
|
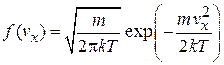 , (2.42а)
, (2.42а)
тогда
 . (2.51)
. (2.51)
Вычисляем интеграл
 ,
,
 ,
,
 ,
,  ,
,  ,
,
получаем
 (2.52)
(2.52)
– плотность потока частиц – число соударений частиц со стенкой единичной площади за 1 с,
учтено
 . (2.46)
. (2.46)
Плотность потока импульса 
 – средний импульс, переносимый за 1с через единичную площадку, перпендикулярную оси z.
– средний импульс, переносимый за 1с через единичную площадку, перпендикулярную оси z.
Частица несет импульс  ,
,
число таких частиц со скоростями  равно
равно
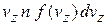 ,
,
тогда
 . (2.53)
. (2.53)
Доказательство:
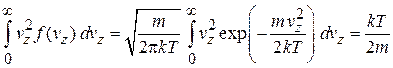 ,
,
 ,
,
 ,
,  ,
,  .
.
Плотность потока энергии 
 – средняя энергия, переносимая за 1с через единичную площадку, перпендикулярную оси z.
– средняя энергия, переносимая за 1с через единичную площадку, перпендикулярную оси z.
Частица несет энергию
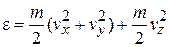 .
.
Учитываем равноправие осей x и y
 .
.
Число проходящих площадку частиц со скоростями  равно
равно
 ,
,
тогда

 .
.
Учитываем
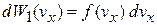 ,
,
 , (2.42)
, (2.42)
 , (2.51)
, (2.51)
 , (2.42б)
, (2.42б)
находим

 . (2.54)
. (2.54)
Следовательно, средняя энергия частицы в потоке  .
.
|
|
|
Это превышает среднюю энергию частицы в газе
 . (2.50)
. (2.50)
Поток не является равновесным состоянием, к нему не применима теорема о распределении энергии по степеням свободы. Больший вклад вносят быстрые частицы.
ВыТЕКАНИЕ газа из отверстия сосуда в вакуум
Направляем ось z перпендикулярно плоскости отверстия площадью S, используем сферические координаты. Распределение в сферических координатах (2.43)

интегрируем по j

– концентрация частиц, движущихся со скоростью  под углом
под углом  .
.

Число вылетающих за 1с частиц под углом q со скоростью v пропорционально эффективной площади отверстия в направлении движения
 ,
,
скорости частиц и концентрации
 ,
,
тогда
 (П.5.7)
(П.5.7)
– число частиц, вылетающих за 1с через отверстие площадью S со скоростями в интервале  под углом в интервале
под углом в интервале  .
.
Интегрируем по v в интервале (0, ¥) и находим число частиц, вылетающих за 1с со всеми скоростями под углом  :
:
 , (П.5.8)
, (П.5.8)
где
 – плотность потока частиц (2.52).
– плотность потока частиц (2.52).
Число частиц, вылетающих в единичный интервал углов около значения q:
 .
.
При q = 0 распределение зануляется из-за обращения в нуль телесного угла, через который идет поток частиц.
Максимум при q = 45°.
Интегрируя (П.5.7) по q в интервале (0, p/2), находим число частиц, вылетающих за 1с по всем направлениям со скоростями в интервале  :
:
 . (П.5.9)
. (П.5.9)
Интегрируя (П.5.8) по углу, или (П.5.9) по скорости, получаем число частиц, вылетающих за секунду со всеми скоростями и под всеми углами:
 . (П.5.10)
. (П.5.10)
Термоэлектронная эмиссия
У элементов первой группы таблицы Менделеева (Li, Na, K, Cu, Rb, Ag, Cs, Au) валентный электрон слабо связан с ядром.
При объединении атомов в кристалл валентные электроны отсоединяются от атомов и становятся свободными. Решетка положительных ионов экранирует заряд электрона на расстояниях порядка периода решетки. В результате электроны не влияют друг на друга и образуют идеальный газ. Их концентрация пропорциональна концентрации узлов решетки  . При
. При  средняя энергия электрона
средняя энергия электрона 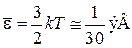 . Кристалл проявляет металлические свойства.
. Кристалл проявляет металлические свойства.
|
|
|
На границе металл–вакуум существует двойной электрический слой, препятствующий выходу электронов. Внешний слой – облако электронов, кратковременно выходящих из металла и возвращающихся назад. Внутренний слой – положительные ионы, не скомпенсированные вышедшими электронами.
Объем металла для электрона оказывается потенциальной ямой с работой выхода А @ 5 эВ. Из  следует, что из металла выходит малая часть электронов, соответствующих хвосту распределения Максвелла.
следует, что из металла выходит малая часть электронов, соответствующих хвосту распределения Максвелла.

Минимальную скорость  , необходимую для выхода, находим из закона сохранения энергии
, необходимую для выхода, находим из закона сохранения энергии
 ,
,
 .
.
По аналогии с выражением
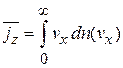 , (2.51)
, (2.51)
находим плотность потока электронов, выходящих из металла:
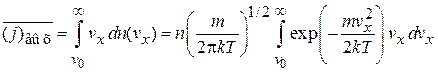 .
.
Интеграл вычисляется заменой аргумента
 ,
,  ,
,
 ,
,
тогда
 , (П.5.12)
, (П.5.12)
где
 – плотность потока электронов, движущихся из объема металла к поверхности;
– плотность потока электронов, движущихся из объема металла к поверхности;
 – вероятность выхода электрона из металла.
– вероятность выхода электрона из металла.
Плотность электрического тока термоэмиссии
 (П.5.13)
(П.5.13)
– формула Ричардсона – Оуэн Вильямс Ричардсон, 1901 г.
|
|
|


