 |
Частица в потенциальной яме
|
|
|
|
Из потенциальной ямы глубиной А может выйти частица благодаря тепловому движению. Получим время τ, за которое частица выходит из ямы.
По определению плотности потока для одной частицы получаем
.
Сравниваем с
, (П.5.12)
получаем
, (П.5.14)
t0 – характерное время выхода при 
. Закон Аррениуса – время выхода возрастает экспоненциально с ростом глубины ямы.
Распределение Больцмана
Рассматривается распределение частиц идеального газа по координатам.
В отсутствии внешнего поля все точки объема с газом равновероятны.
Во внешнем потенциальном поле частица имеет потенциальную энергию 
и на нее действует сила
,
направленная в сторону быстрейшего уменьшения . Сила перемещает частицы газа в определенном направлении, но их разбрасывает тепловое движение. Конкуренция этих тенденций создает равновесное распределение концентрации частиц.
Вывод распределения
Используем каноническое распределение с гамильтонианом частицы
.
Слагаемые с импульсами и координатами разделены, поэтому разделяются распределения по импульсам и координатам
.
Для координат получаем распределение Больцмана
(2.55)
– вероятность обнаружения частицы в элементе объема 
;
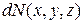– число частиц в элементе объема 
;
N – число частиц в объеме V;
– потенциальная энергия частицы во внешнем поле.
Нормировка вероятности
дает
,
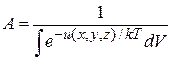тогда
. (2.55а)
Если потенциальная энергия не зависит от x и y, тогда 
, интегрируем (2.55а) по x и y, находим вероятность обнаружения частицы в интервале 
:
; (2.55б)
– плотность вероятности, т. е. вероятность обнаружения частицы в единичном интервале около z;
|
|
|
N –число частиц в объеме V;
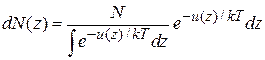(2.56)
– число частиц в интервале .
Мысленно выделяем в объеме газа цилиндр с поперечным сечением 
, образующей вдоль z, и числом частиц 
. В интервале число частиц
,
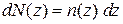концентрация
. (2.56а)
ФормулА Больцмана
Газ в однородном поле тяжести. Сила mg действует на частицу вниз. Тепловая энергия 
раскидывает частицы по разным высотам. Концентрация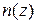 
уменьшается с высотой z.
Потенциальная энергия частицы в поле тяжести
,
m – масса частицы. Для концентрации получаем из (2.56а) формулу Больцмана
, (П.6.1)
– концентрация при 
.
Если N частиц заполняют цилиндр 0 £ z < ¥ с поперечным сечением , тогда вероятность обнаружить частицу в интервале
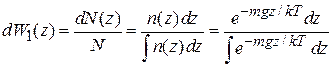, (П.6.2)
где
;
.
Концентрация около точки z
.
Площадь под кривой равна N.
Среднее положение частицы
,
где
, (5.6.2)
.
Число частиц в цилиндре
.
При t = 0°С для воздуха m = 29 кг/кмоль получаем 
км.
При Р = 760 мм р.с. находим число частиц в столбе воздуха с единичным поперечным сечением
.
Число Лошмидта – концентрация у поверхности земли
.
Средняя потенциальная энергия частицы
.
Результат следует также из теоремы о распределении тепловой энергии по степеням свободы. Для одной степени свободы с потенциальной энергией используем
, (2.38)
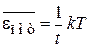. (2.39)
Газ в центрифуге
Центрифуга – цилиндрический сосуд с газом радиусом R, длиной образующей H, вращается вокруг оси с угловой скоростью w. Концентрация увеличивается с удалением от оси.
В системе отсчета, связанной с вращающимся сосудом, на частицу действует центробежная сила 
. Из
,
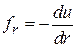находим потенциальную энергию вращения на расстоянии r от оси
.
Из распределения Больцмана
(2.55)
в цилиндрических координатах
|
|
|
, 
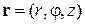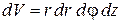
получаем
.
Интегрируем по z и φ
(П.6.2)
– вероятность найти частицу в цилиндрическом слое радиусом r, толщиной dr.
Вероятность найти частицу в единице объема на расстоянии r от оси
,
где
– объем цилиндрического слоя радиусом r, толщиной dr.
Концентрация
,
где N – число частиц в центрифуге. Учитывая (П.6.2), получаем
, (П.6.3)
– концентрация на оси вращения;
– увеличивается при удалении от оси.
Условие нормировки на число частиц в центрифуге
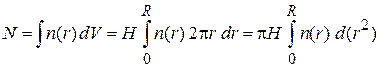
дает
. (П.6.4)
|
|
|
