5.3. Теплофизические свойства

Теплофизические свойства дисперсных металлов исследуются в значительно меньшей мере, нежели их электромагнитные характеристики. Связано это, вероятно, с их еще более высокой, чем у последних, чувствительностью к неизбежной дисперсионной, структурной, физико-химической микронеоднородности порошковых образцов, а также с трудностями корреляции теплофизических характеристик с физико-механическими свойствами дисперсного материала.

В общем приближении дисперсный материал может рассматриваться в виде остова из огромного числа частиц различных размеров иформы, разделенных промежутками, заполненными газом, влагой или тем идругим одновременно [60]. В такой системе теплопередача складывается из трех одновременно действующих процессов - теплопроводности, излучения и конвекции. И осуществляются они посредством теплопроводности, молекулярной теплопроводности и конвекции в пространстве пор, теплопередачи на межфазной границе и излучения от частицы к частице.

Такой сложный тепловой баланс легко смещается под влиянием изменения размеров частиц и связанного с ними размера межчастичных промежутков. Он зависит от природы дисперсного вещества, а при одинаковом его составе - от формы частиц и скульпту­ ры поверхности, определяющих размеров и проводимость контактных

 площадок между частицами. Все это и может служить источником нестабильности результатов измерения теплофизичеких свойиств порошков.

Для измерения коэффициентов теплопроводности и удельной

теплоемкости дисперсных материалов предложено довольно много методов [60-62]. Методы определения тепло- и температуро­ проводности подразделяются на две группы: со стационарным и не­ стационарным тепловым режимом. Каждая из них, в свою оче­ редь, включает в себя методы

пластины, цилиндра и шара в зависимости от формы исследуемого образца. Ясно, что для теплофизических измерений данными методами дисперсные материалы должны быть спрессованы в образцы соответствующей формы. В этом случае в игру вступает фактор пористости твердого тела, оказывающий собственное влияние на его теплофизические характеристики.

Кроме упомянутых  двух

групп, широко используются методы регулярного и квазистационарного режима и калориметрический метод, позволяющий исследовать образец в исходном диспергированном  

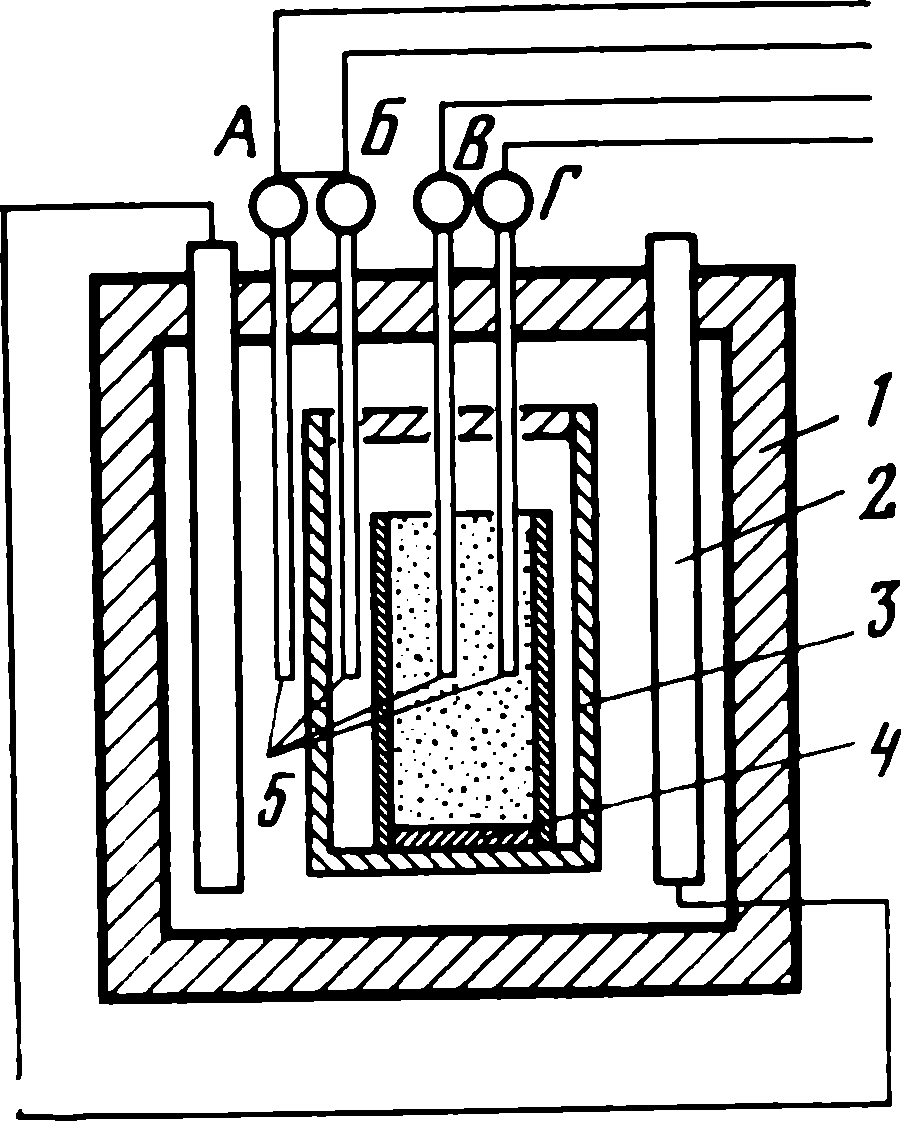
Рис. 5. 5. Схема установки для  измерения теплофизических характеристик дисперсных материалов

1 - печь; 2 - силитовые нагреватели; з - теплозащитный стакан; 4 - кварцевый тигель с исследуемым материалом; 5 - термопары

состоянии. Классическими методами для определения теплоемкости являются балансные методы и методы адиабатического калориметра.

Вероятно, одной из наиболее удобных для комплексного измерения теплофизических характеристик дисперсных тел может считаться автоматизированная установка постоянного теплового потока УПТП (рис. 5. 5) [61]. Она работает на принципе подвода постоянного количества тепла к исследуемому веществу с замером температуры в центре t_ц и на периферии t_п образца, находящегося в тигле 4 (термопары В и Г), и перепада температур ∆ t на диатермической оболочке (термопары А и Б). Исследуемый порошок перед измерениями просушивается при температуре 120° С. Если он обладает малой насыпной плотностью, его целесообразно предварительно спрессовать и из заготовки вырезать образец, возможно ближе отвечающий внутренним размерам тигля 4. Установка перед опытами эталонируется. По результатам  замеров температур рассчитываются значения теплоемкости С₀^Tиз зависимости

C₀ =J/T,                                                                            (5. l6)

где J - теплопотребление материала; Т - температура наг­ рева, 0 С.

Теплопотребление определяется как

Здесь I₁ и I₂- справочные значения [63] теплосодершания двух эталонных веществ; т1, т2, т3 - массы одного и    двух эталонов иисследуемого вещества; z₁, z₂, z₃- время, необходимое для повышения температуры от 0 до Т в опытах с двуvz эталонами иисследуемый веществом.

Кроме того, рассчитываются коэффициенты температуропроводности а итеплопроводности λ. Для этого по кривой изменения во времени температур периферии и оси образца, разбив ее на относительно прямолинейные участки, определяют ∆ t0 = t_п-t_ц

и   сτ = t_цк – t_цн = t_пк  - t_нп - повышение температуры на данном участке за время τ.

Рассчитав ∆ t0 /сτ из временного интервала Фурье-диаграммы [61] получают значения критерия Фурье F_O, через который вычисляется коэффициент температуропроводности

a =F₀R²/τ    ,                                                                            (5. 28)

где R -  радиус тигля с образцом.

  При известноиu             теплоемкости С₀ и насыпной плотности с_н

   диперсного материала его теплопроводность λ  определится из простого выражения

λ = aC₀c_н,                                                                             (5. 29)

Как уже говорилось, при обработке результатов специальное внимание должно быть обращено на учет индивидуальных особенностей порошковых материалов [60-64]. Особенности эти приобретают часто аномальный характер, если размер частиц снижается до ультрадисперсного уровня, на котором решающее влияние на физические свойства порошков начинают оказывать размерные эффекты [38].

Для таких ультрадисперсных систем с высокоразвитой поверхностью особенно высока роль поверхностной энергии, которую важно уметь оценить количественно. Такие данные могут быть получены в результате измерения теплот смачивания порошков металлов жидкостями различной природы. Ими могут быть, например, органические растворители типа бензола, метанола, н-пропанола. Основным измерительным устройством служит микрокалориметр, выдающий результаты в виде термограмм смачивания. Получаемые по ним теплоты указывают на большую чувствителность метода к состоянию и величине удельной поверхности дисперсных тел [59, 65-67].

Теплофизические характеристики могут сниматься с порошков не только в состоянии засыпки, но и после их уплотнения в образцы специальной формы. В этом последнем случае используются методы, позволяющие наряду с термическими определить электрические характеристики порошков. Таков, к примеру, метод точечного контакта [68], обеспечивающий возможность раздельного измерения теплопроводности, удельного электросопротивления и коэффициента Зеебека в различных точках порошкового образца.

Теплофизические свойства могут быть рассчитаны и теоретически. При этом, например, методы расчета теплопроводности порошков во многом сходны с таковыми для электропроводности, поскольку для нее справедливы теоретические исследования проводимости дисперсных смесей методами самосогласованного поля Маккензи-Оделевского, развитыми впоследствии для систем с несовершенными контактами [13-15].

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: