 |
Дополнительный материал (глоссарий, статистические таблицы)
|
|
|
|
Автокорреляция - Автокорреляция – это корреляция (взаимосвязь) между наблюдениями временного ряда и значениями того же ряда, отстоящими на фиксированный интервал времени. При работе с дискретизированными временными рядами проще всего считать, что вычисляется корреляция между двумя множествами наблюдений, одно из которых – исходный ряд, другое – он же, сдвинутый на нужное число точек.
Бинарная переменная - Дихотомическая переменная, значения которой кодируются числами 1 и 0. Как правило, 0 обозначает неудачу или отсутствие, а 1 – успех, наличие. Стандартный пример – бросание монеты, где почему-то выпадение орла всегда обозначают кодом 1.
Дисперсионный анализ - Совокупность моделей и методов, применяемых для анализа зависимости непрерывного отклика от дискретных факторов.
Доверительный интервал - Доверительный интервал для скалярного параметра генеральной совокупности – это отрезок, с большой вероятностью содержащий этот параметр. Эта фраза без дальнейших уточнений бессмысленна. Поскольку границы доверительного интервала оцениваются по выборке, естественна его частотная интерпретация: если много раз брать из генеральной совокупности независимые выборки и по каждой из них оценивать доверительный интервал, то определенная доля этих интервалов “накроет” значение параметра. Доверительный интервал строят так, чтобы доля накрывающих интервалов равнялась доверительному уровню; не путать с уровнем значимости критерия – вещи близкие, но не тождественные. Стандартные значения доверительных уровней: 95%, 90%, 99% и, реже, 99.9%.
Ширина доверительного интервала характеризует степень нашего незнания: слишком широкий доверительный интервал может служить указанием на то, что следует собрать больше данных.
|
|
|
Доверительные интервалы дают больше информации о параметре, чем простая точечная оценка, поскольку отграничивают сразу целую совокупность допустимых значений.
См. тж. доверительные границы.
Корреляция - Когда говорят, что две случайные переменные коррелированны, имеют в виду, как правило, что они друг с другом как-то связаны.
Стандартной мерой связи переменных является коэффициент корреляции. Следует, однако, помнить, что он измеряет лишь силу линейной связи и лишь в случае, когда обе переменные числовые.
См. тж. мера связи.
Коэффициент вариации (случайной величины или распределения вероятностей) - Отношение стандартного отклонения к математическому ожиданию (или его абсолютной величине) случайной величины,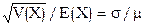 
, а также отношение s/m оценок этих параметров. Коэффициент вариации является одной из мер разброса данных.
Примечания:
1. Это отношение часто выражают в процентах.
В качестве альтернативы иногда используется термин “относительное стандартное отклонение”, но такое словоупотребление не рекомендуется.
Коэффициент корреляции - это число, заключенное между -1 и 1, которое измеряет силу линейной связи двух случайных переменных. Положительное значение коэффициента корреляции означает, что с ростом одной из переменных другая также растет, с убыванием одной из них убывает и другая. Отрицательное значение означает, что с ростом одной из переменных другая убывает, с убыванием одной из них другая растет. Коэффициент корреляции, равный нулю, означает, что между нашими переменными отсутствует линейная связь.
Статистические таблицы
Критерий Дарбина-Уотсона (d). Значения d L и d U при 5% уровне значимости.
| n | k =1 | k =2 | k =3 | k =4 | k =5 | |||||
| d L | d U | d L | d U | d L | d U | d L | d U | d L | d U | |
| 0,95 | 1,23 | 0,83 | 1,40 | 0,71 | 1,61 | 0,59 | 1,84 | 0,48 | 2,09 | |
| 0,98 | 1,24 | 0,86 | 1,40 | 0,75 | 1,59 | 0,64 | 1,80 | 0,53 | 2,03 | |
| 1,01 | 1,25 | 0,90 | 1,40 | 0,79 | 1,58 | 0,68 | 1,77 | 0,57 | 1,98 | |
| 1,03 | 1,26 | 0,93 | 1,40 | 0,82 | 1,56 | 0,72 | 1,74 | 0,62 | 1,93 | |
| 1,06 | 1,28 | 0,96 | 1,41 | 0,86 | 1,55 | 0,76 | 1,72 | 0,66 | 1,90 | |
| 1,08 | 1,28 | 0,99 | 1,41 | 0,89 | 1,54 | 0,79 | 1,70 | 0,70 | 1,87 | |
| 1,10 | 1,30 | 1,01 | 1,41 | 0,92 | 1,54 | 0,83 | 1,69 | 0,73 | 1,84 | |
| 1,12 | 1,31 | 1,04 | 1,42 | 0,95 | 1,54 | 0,86 | 1,68 | 0,77 | 1,82 | |
| 1,14 | 1,32 | 1,06 | 1,42 | 0,97 | 1,54 | 0,89 | 1,67 | 0,80 | 1,80 | |
| 1,16 | 1,33 | 1,08 | 1,43 | 1,00 | 1,54 | 0,91 | 1,66 | 0,83 | 1,79 | |
| 1,18 | 1,34 | 1,10 | 1,43 | 1,02 | 1,54 | 0,94 | 1,65 | 0,86 | 1,77 | |
| 1,19 | 1,35 | 1,12 | 1,44 | 1,04 | 1,54 | 0,96 | 1,65 | 0,88 | 1,76 | |
| 1,21 | 1,36 | 1,13 | 1,44 | 1,06 | 1,54 | 1,99 | 1,64 | 0,91 | 1,75 | |
| 1,22 | 1,37 | 1,15 | 1,45 | 1,08 | 1,54 | 1,01 | 1,64 | 0,93 | 1,74 | |
| 1,24 | 1,38 | 1,17 | 1,45 | 1,10 | 1,54 | 1,03 | 1,63 | 0,96 | 1,73 | |
| 1,25 | 1,38 | 1,18 | 1,46 | 1,12 | 1,54 | 1,05 | 1,63 | 0,98 | 1,73 | |
| 1,26 | 1,39 | 1,20 | 1,47 | 1,13 | 1,55 | 1,07 | 1,63 | 1,00 | 1,72 | |
| 1,27 | 1,40 | 1,21 | 1,47 | 1,15 | 1,55 | 1,08 | 1,63 | 1,02 | 1,71 | |
| 1,28 | 1,41 | 1,22 | 1,48 | 1,16 | 1,55 | 1,10 | 1,63 | 1,04 | 1,71 | |
| 1,29 | 1,41 | 1,24 | 1,48 | 1,17 | 1,55 | 1,12 | 1,63 | 1,06 | 1,70 | |
| 1,30 | 1,42 | 1,25 | 1,48 | 1,19 | 1,55 | 1,13 | 1,63 | 1,07 | 1,70 | |
| 1,31 | 1,43 | 1,26 | 1,49 | 1,20 | 1,56 | 1,15 | 1,63 | 1,09 | 1,70 | |
| 1,32 | 1,43 | 1,27 | 1,49 | 1,21 | 1,56 | 1,16 | 1,62 | 1,10 | 1,70 | |
| 1,33 | 1,44 | 1,28 | 1,50 | 1,23 | 1,56 | 1,17 | 1,62 | 1,12 | 1,70 | |
| 1,34 | 1,44 | 1,29 | 1,50 | 1,24 | 1,56 | 1,19 | 1,63 | 1,13 | 1,69 | |
| 1,35 | 1,45 | 1,30 | 1,51 | 1,25 | 1,57 | 1,20 | 1,63 | 1,15 | 1,69 | |
| 1,39 | 1,48 | 1,34 | 1,53 | 1,30 | 1,58 | 1,25 | 1,63 | 1,21 | 1,69 | |
| 1,42 | 1,50 | 1,38 | 1,54 | 1,34 | 1,59 | 1,30 | 1,64 | 1,26 | 1,69 | |
| 1,45 | 1,52 | 1,41 | 1,56 | 1,37 | 1,60 | 1,33 | 1,64 | 1,30 | 1,69 | |
| 1,47 | 1,54 | 1,44 | 1,57 | 1,40 | 1,61 | 1,37 | 1,65 | 1,33 | 1,69 | |
| 1,49 | 1,55 | 1,46 | 1,59 | 1,43 | 1,62 | 1,40 | 1,66 | 1,36 | 1,69 | |
| 1,51 | 1,57 | 1,48 | 1,60 | 1,45 | 1,63 | 1,42 | 1,66 | 1,39 | 1,70 | |
| 1,53 | 1,58 | 1,50 | 1,61 | 1,47 | 1,64 | 1,45 | 1,67 | 1,42 | 1,70 | |
| 1,54 | 1,59 | 1,52 | 1,62 | 1,49 | 1,65 | 1,47 | 1,67 | 1,44 | 1,70 | |
| 1,56 | 1,60 | 1,53 | 1,63 | 1,51 | 1,65 | 1,49 | 1,68 | 1,46 | 1,71 | |
| 1,57 | 1,61 | 1,55 | 1,64 | 1,53 | 1,66 | 1,50 | 1,69 | 1,48 | 1,71 | |
| 1,58 | 1,62 | 1,65 | 1,65 | 1,54 | 1,67 | 1,52 | 1,69 | 1,50 | 1,71 | |
| 1,59 | 1,63 | 1,67 | 1,65 | 1,55 | 1,67 | 1,53 | 1,70 | 1,51 | 1,72 |
|
|
|
n - число наблюдений, k - число объясняющих переменных
Таблица критических величин n u критерия последовательности знаков
| n 1 | n 2 | ||||||||||||||||||
|
|
|
| n 1 | n 2 | ||||||||||||||||||
|
|
|
Двусторонние квантили t - распределения Стьюдента
| m | a | ||||||
| 0,10 | 0,05 | 0,025 | 0,020 | 0,010 | 0,005 | 0,001 | |
| 6,314 | 12,706 | 25,452 | 31,821 | 63,657 | 127,3 | 636,6 | |
| 2,920 | 4,303 | 6,205 | 6,965 | 9,925 | 14,089 | 31,598 | |
| 2,353 | 3,182 | 4,177 | 4,541 | 5,841 | 7,453 | 12,941 | |
| 2,132 | 2,776 | 3,495 | 3,747 | 4,604 | 5,597 | 8,610 | |
| 2,015 | 2,571 | 3,163 | 3,365 | 4,032 | 4,773 | 6,859 | |
| 1,943 | 2,447 | 2,969 | 3,143 | 3,707 | 4,317 | 5,959 | |
| 1,895 | 2,365 | 2,841 | 2,998 | 3,499 | 4,029 | 5,405 | |
| 1,860 | 2,306 | 2,752 | 2,896 | 3,355 | 3,833 | 5,041 | |
| 1,833 | 2,262 | 2,685 | 2,821 | 3,250 | 3,690 | 4,781 | |
| 1,812 | 2,228 | 2,634 | 2,764 | 3,169 | 3,581 | 4,587 | |
| 1,782 | 2,179 | 2,560 | 2,681 | 3,055 | 3,428 | 4,318 | |
| 1,761 | 2,145 | 2,510 | 2,624 | 2,977 | 3,326 | 4,140 | |
| 1,746 | 2,120 | 2,473 | 2,583 | 2,921 | 3,252 | 4,015 | |
| 1,734 | 2,101 | 2,445 | 2,552 | 2,878 | 3,193 | 3,922 | |
| 1,725 | 2,086 | 2,423 | 2,528 | 2,845 | 3,153 | 3,849 | |
| 1,717 | 2,074 | 2,405 | 2,508 | 2,819 | 3,119 | 3,792 | |
| 1,711 | 2,064 | 2,391 | 2,492 | 2,797 | 3,092 | 3,745 | |
| 1,706 | 2,056 | 2,379 | 2,479 | 2,779 | 3,067 | 3,707 | |
| 1,701 | 2,048 | 2,369 | 2,467 | 2,763 | 3,047 | 3,674 | |
| 1,697 | 2,042 | 2,360 | 2,457 | 2,750 | 3,030 | 3,646 | |
| ¥ | 1,645 | 1,960 | 2,241 | 2,326 | 2,576 | 2,807 | 3,291 |
m - число степеней свободы
Квантили распределения c2
| Число степеней свободы | Уровень значимости | |||||
| 0,50 | 0,30 | 0,20 | 0,10 | 0,05 | 0,01 | |
| 0,455 | 1,074 | 1,642 | 2,706 | 3,841 | 6,635 | |
| 1,386 | 2,408 | 3,219 | 4,605 | 5,991 | 9,210 | |
| 2,366 | 3,665 | 4,642 | 6,251 | 7,815 | 11,341 | |
| 3,357 | 4,878 | 5,989 | 7,779 | 9,488 | 13,277 | |
| 4,351 | 6,064 | 7,289 | 9,236 | 11,070 | 15,086 | |
| 5,348 | 7,231 | 8,558 | 10,645 | 12,592 | 16,812 | |
| 6,346 | 8,383 | 9,803 | 12,017 | 14,067 | 18,475 | |
| 7,344 | 9,524 | 11,030 | 13,362 | 15,507 | 20,090 | |
| 8,343 | 10,656 | 12,242 | 14,684 | 16,919 | 21,666 | |
| 9,342 | 11,781 | 13,442 | 15,987 | 18,307 | 23,209 | |
| 10,341 | 12,899 | 14,631 | 17,272 | 19,675 | 24,725 | |
| 11,340 | 14,011 | 15,812 | 18,549 | 21,026 | 26,217 | |
| 12,340 | 15,119 | 16,985 | 19,812 | 22,362 | 27,688 | |
| 13,339 | 16,222 | 18,151 | 21,064 | 23,685 | 29,141 | |
| 14,339 | 18,322 | 19,311 | 22,307 | 24,996 | 30,578 | |
| 15,338 | 18,418 | 20,465 | 23,542 | 26,296 | 32,000 | |
| 17,338 | 20,601 | 22,760 | 25,989 | 28,869 | 34,805 | |
| 19,337 | 22,775 | 25,038 | 28,412 | 31,410 | 37,566 | |
| 23,337 | 27,096 | 29,553 | 33,196 | 36,415 | 42,980 | |
| 29,336 | 33,530 | 36,250 | 40,256 | 43,773 | 50,892 |
|
|
|
Если число степеней свободы больше 30, то выражение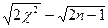 
можно рассматривать как переменную со стандартным нормальным распределением, где n - число степеней свободы.
95% квантили распределения Фишера F (n 1, n 2)
| n 2 | n 1 | ||||||||||||||||||
| ¥ | |||||||||||||||||||
| 18,5 | 19,0 | 19,2 | 19,2 | 19,3 | 19,3 | 19,4 | 19,4 | 19,4 | 19,4 | 19,4 | 19,4 | 19,4 | 19,5 | 19,5 | 19,5 | 19,5 | 19,5 | 19,5 | |
| 10,1 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,89 | 8,85 | 8,81 | 8,79 | 8,74 | 8,70 | 8,66 | 8,64 | 8,62 | 8,59 | 8,57 | 8,55 | 8,53 | |
| 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,09 | 6,04 | 6,00 | 5,96 | 5,91 | 5,86 | 5,80 | 5,77 | 5,75 | 5,72 | 5,69 | 5,66 | 5,63 | |
| 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,88 | 4,82 | 4,77 | 4,74 | 4,68 | 4,62 | 4,56 | 4,53 | 4,50 | 4,46 | 4,43 | 4,40 | 4,37 | |
| 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,21 | 4,15 | 4,10 | 4,06 | 4,00 | 3,94 | 3,87 | 3,84 | 3,81 | 3,77 | 3,74 | 3,70 | 3,67 | |
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,79 | 3,73 | 3,68 | 3,64 | 3,57 | 3,51 | 3,44 | 3,41 | 3,38 | 3,34 | 3,30 | 3,27 | 3,23 | |
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,50 | 3,44 | 3,39 | 3,35 | 3,28 | 3,22 | 3,15 | 3,12 | 3,08 | 3,04 | 3,01 | 2,97 | 2,93 | |
| 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,29 | 3,23 | 3,18 | 3,14 | 3,07 | 3,01 | 2,94 | 2,90 | 2,86 | 2,83 | 2,79 | 2,75 | 2,71 | |
| 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,14 | 3,07 | 3,02 | 2,98 | 2,91 | 2,85 | 2,77 | 2,74 | 2,70 | 2,66 | 2,62 | 2,58 |  2,54
| |
| 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 3,01 | 2,95 | 2,90 | 2,85 | 2,79 | 2,72 | 2,65 | 2,61 | 2,57 | 2,53 | 2,49 | 2,45 | 2,40 | |
| 4,75 | 3,89 | 3,49 | 3,26 | 3,11 | 3,00 | 2,91 | 2,85 | 2,80 | 2,75 | 2,69 | 2,62 | 2,54 | 2,51 | 2,47 | 2,43 | 2,38 | 2,34 | 2,30 | |
| 4,67 | 3,81 | 3,41 | 3,18 | 3,03 | 2,92 | 2,83 | 2,77 | 2,71 | 2,67 | 2,60 | 2,53 | 2,46 | 2,42 | 2,38 | 2,34 | 2,30 | 2,25 | 2,21 | |
| 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,76 | 2,70 | 2,65 | 2,60 | 2,53 | 2,46 | 2,39 | 2,35 | 3,31 | 2,27 | 2,22 | 2,18 | 2,13 | |
| 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,71 | 2,64 | 2,59 | 2,54 | 2,48 | 2,40 | 2,33 | 2,29 | 2,25 | 2,20 | 2,16 | 2,11 | 2,07 | |
| 4,49 | 3,53 | 3,24 | 3,01 | 2,85 | 2,74 | 2,66 | 2,59 | 2,54 | 2,49 | 2,42 | 2,35 | 2,28 | 2,24 | 2,19 | 2,15 | 2,11 | 2,06 | 2,01 | |
| 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,58 | 2,51 | 2,46 | 2,41 | 2,34 | 2,27 | 2,19 | 2,15 | 2,11 | 2,06 | 2,02 | 1,97 | 1,92 | |
| 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,51 | 2,45 | 2,39 | 2,35 | 2,28 | 2,20 | 2,12 | 2,08 | 2,04 | 1,99 | 1,95 | 1,90 | 1,84 | |
| 4,30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,46 | 2,40 | 2,34 | 2,30 | 2,23 | 2,15 | 2,07 | 2,03 | 1,98 | 1,94 | 1,89 | 1,84 | 1,78 | |
| 4,26 | 3,40 | 3,01 | 2,78 | 2,62 | 2,51 | 2,42 | 2,36 | 2,30 | 2,25 | 2,18 | 2,11 | 2,03 | 1,98 | 1,94 | 1,89 | 1,84 | 1,79 | 1,73 | |
| 4,24 | 3,39 | 2,99 | 2,76 | 2,60 | 2,49 | 2,40 | 2,34 | 2,28 | 2,24 | 2,16 | 2,09 | 2,01 | 1,96 | 1,92 | 1,87 | 1,82 | 1,77 | 1,71 | |
| 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,33 | 2,27 | 2,21 | 2,16 | 2,09 | 2,01 | 1,93 | 1,89 | 1,84 | 1,79 | 1,74 | 1,68 | 1,62 | |
| 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,25 | 2,18 | 2,12 | 2,08 | 2,00 | 1,92 | 1,84 | 1,79 | 1,74 | 1,69 | 1,64 | 1,58 | 1,51 | |
| 4,00 | 3,15 | 2,76 | 2,53 | 2,37 | 2,25 | 2,17 | 2,10 | 2,04 | 1,99 | 1,92 | 1,84 | 1,75 | 1,70 | 1,65 | 1,59 | 1,53 | 1,47 | 1,39 | |
| 3,92 | 3,07 | 2,68 | 2,45 | 2,29 | 2,18 | 2,09 | 2,02 | 1,96 | 1,91 | 1,83 | 1,75 | 1,66 | 1,61 | 1,55 | 1,50 | 1,43 | 1,35 | 1,25 | |
| ¥ | 3,84 | 3,00 | 2,60 | 2,37 | 2,21 | 2,10 | 2,01 | 1,94 | 1,88 | 1,83 | 1,75 | 1,67 | 1,57 | 1,52 | 1,46 | 1,39 | 1,32 | 1,22 | 1,00 |
n 1 – число степеней свободы числителя, n 2 – число степеней свободы знаменателя
[1] Использованы материалы учебного пособия Арженовского С.В., Федосовой О.Н. Эконометрика:Учебное пособие/Рост. гос. экон. унив. - Ростов н/Д., - 2002.
[2] Стандартная ошибка дает только общую оценку степени точности коэффициента регрессии. Ясно, что, чем больше будет величина дисперсии случайного члена (и соответственно ее оценка – выборочная дисперсия остатков), тем существеннее величина стандартной ошибки, и с большей вероятностью можно говорить о том, что полученная оценка неточна.
[3] Другой возможный путь решения - это известная схема управляемого эксперимента – см., например: Джонсон Н., Лион Ф. Статистика и планирование эксперимента в технике и науке. В 2-х т. М.: Мир, 1980.
[4] С использованием матричной алгебры можно получить аналитическую формулу для оценок коэффициентов, см., например: Магнус Я.Р, Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. М.: Дело, 2000. С. 60-63.
[5] Подробнее смотри Эконометрика: Учебник/ Под. ред. Елисеевой И.И. М.:Финансы и статистика, 2001. С.112-120.
[6] См., например: [1], с. 658-661.
6 Этот абзац может быть опущен без ущерба для дальнейшего усвоения материала пособия.
7 Пример взят из [4]
8 Пример из [3].
9 См. [7], с. 235-238.
7 Использованы материалы учебно-методического пособия Ниворожкиной Л.И., Арженовского С.В., Федосовой О.Н. Эконометрика: Методические указания и задания к контрольной работе/Рост. гос. экон. ун-т. - Ростов н/Д, 2003.
|
|
|
