 |
2 електричні кола однофазного. синусоїдного струму. 2. 1 теоретичні відомості
|
|
|
|
2 ЕЛЕКТРИЧНІ КОЛА ОДНОФАЗНОГО
СИНУСОЇДНОГО СТРУМУ
2. 1 ТЕОРЕТИЧНІ ВІДОМОСТІ
У сучасній техніці використовуються синусоїдні струми широкого діапазону частот. Джерелами синусоїдної ЕРС промислової частоти (50 Гц) є синхронні генератори, встановлені на електричних станціях. Генерування синусоїдних ЕРС високих частот здійснюється за допомогою електронних генераторів.
Величинами, які характеризують синусоїдні ЕРС, напругу і струм є амплітуда, миттєве і діюче значення, період, частота, фаза, зсув за фазою.
Миттєві значення ЕРС, напруги і струму змінюються в часі за синусоїдним законом
 ,
,  ,
, 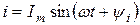
і визначаються трьома основними величинами: амплітудою (найбільше значення миттєвої величини)  ,
,  ,
, 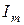 , кутовою частотою
, кутовою частотою 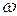 і початковою фазою
і початковою фазою  ,
, 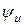 ,
,  . Аргумент функції синуса називають фазою (
. Аргумент функції синуса називають фазою ( 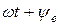 – фаза ЕРС,
– фаза ЕРС, 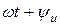 – фаза напруги,
– фаза напруги, 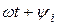 – фаза струму). Для прикладу на рисунку2. 1, а відображені синусоїдні величини напруги і струму:
– фаза струму). Для прикладу на рисунку2. 1, а відображені синусоїдні величини напруги і струму:
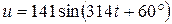 В,
В,  А,
А,
які змінюються з кутовою частотою 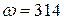 рад/с.
рад/с.
Відмітимо, що додатну початкову фазу відкладають від початку координат ліворуч, а від’ємну – праворуч. Вздовж осі абсцис відкладають час  , або пропорційну йому величину
, або пропорційну йому величину  .
.
Час, впродовж якого здійснюється одне повне коливання, називається періодом  . Величина, обернена до періоду, називається частотою
. Величина, обернена до періоду, називається частотою  . Одиниця вимірювання частоти – герц (Гц) – кількість коливань за 1 с.
. Одиниця вимірювання частоти – герц (Гц) – кількість коливань за 1 с.
Між кутовою частотою 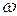 , періодом
, періодом  і частотою
і частотою 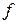 справедливе співвідношення
справедливе співвідношення 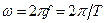 . При кутовій частоті
. При кутовій частоті 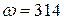 рад/с:
рад/с:
 Гц,
Гц,  с.
с.
Кут зсуву фаз між напругою і струмом для розглянутого прикладу: 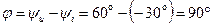 .
.
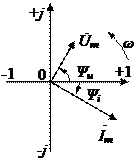 | |||
 | |||
а) б)
|
|
|
Рисунок 2. 1 – Часові залежності (а) і векторна діаграма (б)
синусоїдних напруги і струму
У загальному випадку процеси, які відбуваються в колах змінного струму, складніші в порівнянні з процесами в колах постійного струму. Це обумовлено тим, що в колах змінного струму відбуваються безперервні зміни струму і напруги, а взаємозв’язок між ними описується не алгебраїчними, а диференційними рівняннями. Дійсно, миттєві значення спаду напруги на активному опорі 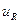 , індуктивності
, індуктивності 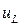 і ємності
і ємності  при проходженні через них струму
при проходженні через них струму 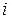 , дорівнюють:
, дорівнюють:
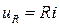 ,
, 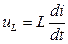 ,
,  .
.
Для синусоїдного струму 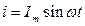 миттєві значення спадів напруг будуть відповідно дорівнювати:
миттєві значення спадів напруг будуть відповідно дорівнювати:
 ,
, 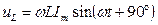 ,
, 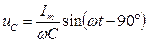 .
.
Як видно із останніх виразів, напруга на активному опорі збігається за фазою зі струмом, на індуктивності – випереджує, а на ємності – відстає на кут 90°. Величини  ,
,  називають відповідно індуктивним і ємнісним опорами. Слід звернути увагу на те, що індуктивний опір збільшується при збільшенні частоти, а ємнісний, навпаки, зменшується. При цьому індуктивний опір змінюється пропорційно, а ємнісний – обернено пропорційний до частоти.
називають відповідно індуктивним і ємнісним опорами. Слід звернути увагу на те, що індуктивний опір збільшується при збільшенні частоти, а ємнісний, навпаки, зменшується. При цьому індуктивний опір змінюється пропорційно, а ємнісний – обернено пропорційний до частоти.
Для розрахунку електричних кіл синусоїдного струму використовується символічний метод. Він полягає в переході від диференційних рівнянь, до рівнянь, складених у комплексній формі відносно комплексних амплітуд струму, напруги і ЕРС:
 ;
;  ;
;  .
.
Роз’язання задачі доцільно супроводжувати побудовою векторних діаграм, які відображають сукупність векторів ЕРС, напруг і струмів кола, зображених для моменту часу 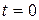 . Довжина векторів визначається амплітудою ЕРС, напруги або струму, а кути, які відраховуються від дійсної осі, дорівнюють початковим фазам. Величини
. Довжина векторів визначається амплітудою ЕРС, напруги або струму, а кути, які відраховуються від дійсної осі, дорівнюють початковим фазам. Величини  ,
, 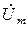 і
і 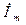 називають комплексними амплітудами відповідно ЕРС, напруги і струму. На рис. 2. 1, б зображена векторна діаграма напруги
називають комплексними амплітудами відповідно ЕРС, напруги і струму. На рис. 2. 1, б зображена векторна діаграма напруги  В і струму
В і струму  А. Комплексні амплітуди напруги і струму відповідно дорівнюють:
А. Комплексні амплітуди напруги і струму відповідно дорівнюють:
|
|
|
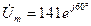 В,
В, 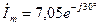 А.
А.
Змінні ЕРС, напруги і струми під час розрахунків замінюють еквівалентними незмінними в часі величинами – діючими значеннями:
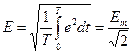 ,
, 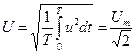 ,
,  .
.
Для даного прикладу діючі значення дорівнюють:
 В;
В;  А.
А.
Комплексні діючі значення напруги і струму
 В;
В;  А.
А.
Відношення комплексної напруги  до комплексного струму
до комплексного струму  називають комплексним опором кола
називають комплексним опором кола
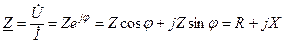 ,
,
де 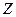 ,
,  – модуль і аргумент комплексного опору;
– модуль і аргумент комплексного опору;
 ,
,  – дійсна і уявна складові комплексного опору.
– дійсна і уявна складові комплексного опору.
Комплексні опори елементів 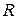 ,
,  і
і 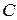 записують як
записують як
 ,
, 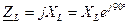 ,
,  .
.
Величину, обернену до комплексного опору, називають комплексною провідністю
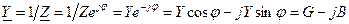 ,
,
де  ,
,  ,
,  – активна, реактивна і повна провідності кола.
– активна, реактивна і повна провідності кола.
Перший і другий закони Кірхгофа у комплексній формі записують так
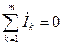 ,
,  ,
,
де 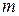 – кількість віток, які сходяться у вузлі;
– кількість віток, які сходяться у вузлі;
 – кількість віток, які входять у замкнений контур.
– кількість віток, які входять у замкнений контур.
Під час розрахунку кіл комплексним методом використовують комплексні числа. Будь-яке комплексне число 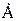 можна відобразити в трьох формах запису – алгебраїчній, тригонометричній та показниковій
можна відобразити в трьох формах запису – алгебраїчній, тригонометричній та показниковій
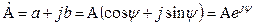 ,
,
де  ,
,  – дійсна і уявна частини комплексного числа;
– дійсна і уявна частини комплексного числа;
 ,
,  – модуль і аргумент комплексного числа.
– модуль і аргумент комплексного числа.
Додавання і віднімання комплексних чисел зручно виконувати, використавши алгебраїчну форму запису
 ,
,
а ділення і множення – показникову форму запису
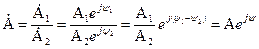 ,
,
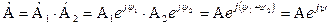 .
.
У зв’язку з тим, що виникає необхідність у переході від однієї форми запису комплексного числа до іншої, взаємозв’язки між модулем, аргументом, дійсною та уявною частинами комплексного числа наступні:
 ,
,  ,
,  .
.
При знаходженні аргумента доцільно визначити розміщення вектора комплексного числа на комплексній площині. Комплексне число, наприклад 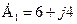 , знаходиться в першому квадранті площини (рисунку 2. 2, а). Тоді аргумент
, знаходиться в першому квадранті площини (рисунку 2. 2, а). Тоді аргумент  .
.
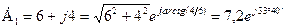 .
.
Комплексне число, наприклад  , знаходиться в четвертому квадранті площини (рисунку 2. 2, б). Тоді аргумент
, знаходиться в четвертому квадранті площини (рисунку 2. 2, б). Тоді аргумент 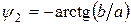
 .
.
Комплексні числа,  ,
, 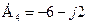 знаходяться в другому і третьому квадрантах (рис. 2. 2, в і г). Аргументи
знаходяться в другому і третьому квадрантах (рис. 2. 2, в і г). Аргументи  і
і 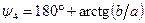 , при цьому
, при цьому
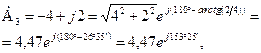
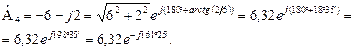
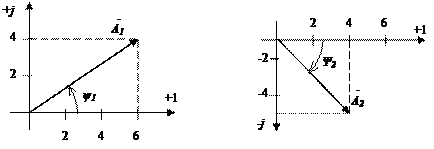
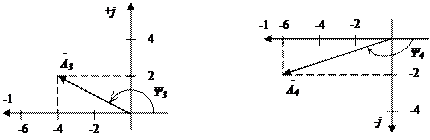 а) б)
а) б)
|
|
|


