 |
2.5 Прочностной расчет элементов привода
|
|
|
|
2. 5 Прочностной расчет элементов привода
2. 5. 1 Проверочный расчет зубчатой муфты
Поскольку износ является основным критерием работоспособности зубчатой муфты, проверочный расчет муфты проводят по напряжениям смятия
(24)
где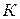 
– коэффициент динамичности,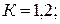 
– крутящий момент на муфте, 
– делительный диаметр зубчатого зацепления муфты,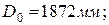 
– длина зуба,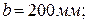 
– допускаемое напряжение смятия, 
Данная муфта проходит по пределу прочности, так как напряжение смятия меньше допустимых.
2. 5. 2 Проверочный расчет редуктора
Материалы: шестерня 38ХГН – НВ240;
колесо 38ХГН – НВ210
Допустимое контактное напряжение
(25)
где 
- предел контактной усталости поверхности зубьев, соответствующий ба-
зовому числу циклов напряжений,
для колеса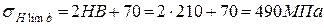 
для шестерни 
- коэффициент безопасности, 
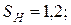
- коэффициент, учитывающий шероховатость сопряженных поверхностей
зубьев,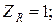 
- коэффициент, учитывающий окружную скорость передачи, 
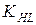- коэффициент долговечности, 
Расчетное контактное напряжение
(26)
где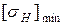 
- минимальное допустимое напряжение, 
;
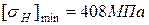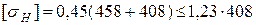
Допустимое напряжение изгиба
(27)
где 
- предел выносливости зубьев при изгибе, соответствующий базовому
числу циклов напряжений, для шестерни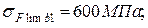 
для колеса 
- коэффициент безопасности,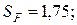 
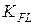- коэффициент долговечности, 
|
|
|
- коэффициент, учитывающий влияние двухстороннего приложения нагруз-
ки на зубья, 
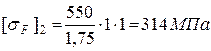
2. 5. 3 Расчет быстроходного вала редуктора
Для расчета строим схему нагрузок на вал рисунок 19.
Окружная сила, действующая на одну из частей (правую или левую) шевронного колеса
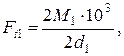(28)
где 
- номинальный момент электродвигателя, 
- делительный диаметр шестерни, 
Радиальная сила, действующая на зубчатое колесо шевронной передачи
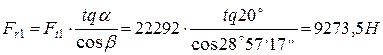(29)
Определяем реакцию в опорах в плоскости ХУ
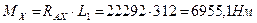
Определяем реакции в опорах в плоскости XZ
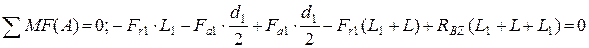
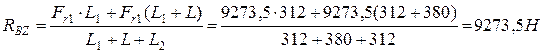
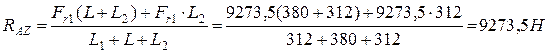
Определяем моменты
Максимальный эквивалентный момент в точке С равен
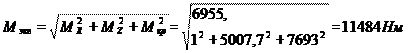(30)
Расчет вала в опасном сечении
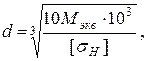(31)
где 
допустимое напряжение на изгибе, 
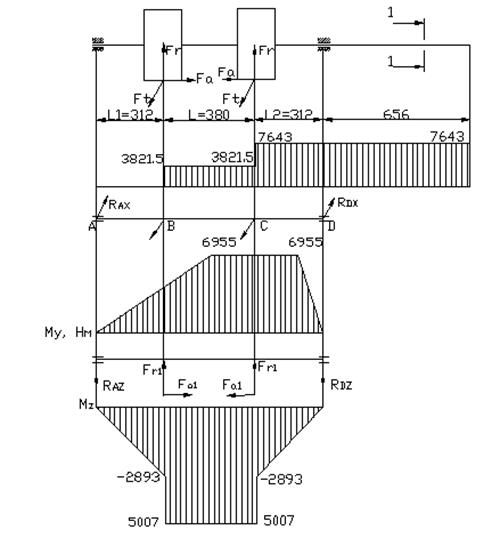
Рисунок 19 – Схема нагрузок на быстроходный вал редуктора
2. 5. 4 Расчет тихоходного вала редуктора
Окружное усилие на тихоходном валу редуктора
(32)
Осевое усилие на тихоходном валу редуктора
(33)
Радиальное усилие на тихоходном валу редуктора
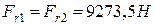(34)
Определяем реакции опор в плоскости ХУ рисунок 2. 18
Определяем момент
Определяем реакции опор в плоскости XZ
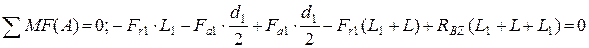
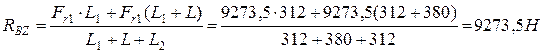
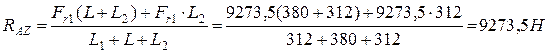
Определяем моменты
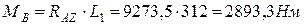
Максимальный эквивалентный момент в точке С равен
(35)
Расчет вала в опасном сечении
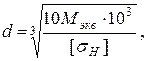(36)
где допустимое напряжение на изгибе,
Рисунок 20 – Схема нагрузок тихоходного вала редуктора
2. 6 Расчет тихоходного вала на прочность с учетом надёжности методом «непревышения»
Успешное решение вопросов надёжности металлургического оборудования возможно лишь при проведении широкой исследовательской работы, связанной с отбором и обработкой достоверной статистической информации об отказах в процессе эксплуатации.
|
|
|
При обычных расчетах на прочность деталей металлургических машин на основе методов теории сопротивления материалов полагают, что деталь будет работать безотказно, когда нагрузка Q не превышает прочности R материала детали.
Однако нагрузка и прочность деталей зависят от большого числа факторов, поэтому R и Q являются случайными величинами и для оценки вероятности безотказной работы (надежности) детали необходимо знать законы распределения R и Q.
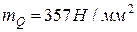
Математическое ожидание
(37)
Дисперсия
(38)
(39)
Так как R и Q подчиняются нормальным законам распределения, то и композиция этих законов также будет нормальным законом с плотностью вероятности
Находим промежуточные точки плотности распределения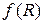 
и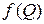 
, заносим их в таблицу 15 и строим график плотности распределения прочности R и нагрузки Q
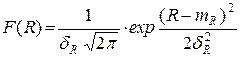(40)
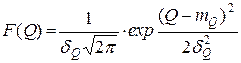(41)
Таблица 15 – Плотности распределения f(R) и f(Q)
| mQ | mR | ||||||
| Q | 102, 36 | 92, 36 | 82, 36 | R | |||
| f(Q) | 0, 075 | 0, 044 | 0, 009 | f(R) | 0, 133 | 0, 082 | 0, 018 |
Соотношения между плотностями распределения 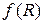и 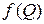приведены на рисунке 21. Заштрихованный участок показывает область перекрытия распределения Q и R, которая характеризует вероятность отказа детали.
Вычисляем
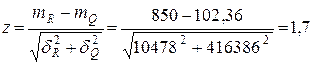(42)
Из приложения 3 [5, с. 409] находят значения нормированной функции Лапласа для 
получают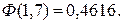 
Вероятность безотказной работы вала
(43)
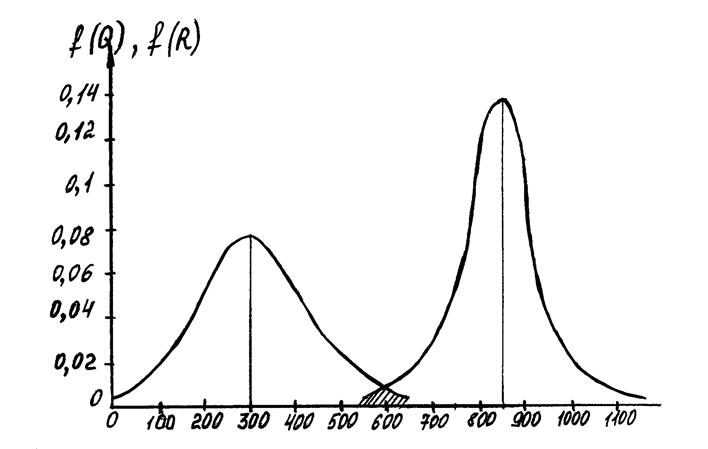
Рисунок 21 – Плотности распределения нагрузки Q и прочности R
|
|
|
