 |
dQ = p×En×dF1 = p×dQn.
|
|
|
|
dQ = p× En× dF1 = p× dQn.
Приравняв правые части полученной зависимости и уравнения Стефана - Больцмана для элементарной поверхности dF1, определяем неизвестную En,
En = E / p =. (13)
Из этого уравнения следует, что плотность излучения в направлении нормали в p раз меньше полной плотности излучения тела.
После подстановки полученного значения En из уравнения (13) в уравнение (12) последнее примет вид
d2Qq = × dw× dF1× cosq.
Это уравнение служит основой для расчета лучистого теплообмена между поверхностями конечных размеров.
Закон Ламберта строго справедлив для абсолютно черного тела. Для шероховатых тел этот закон подтверждается опытом лишь для q = 0 - 60о. При q > 60о значение eq = Еq / Е0 q = f (q) уменьшается и стремится к нулю. Однако это уменьшение практического значения не имеет, ибо среднее значение 
Более резкое отклонение от закона Ламберта наблюдается для полированных металлов. При 40о< q < 80о значение eq увеличивается, а при q > 80о оно стремится к нулю. В этом случае среднее значение  = 1, 2× eq=0.
= 1, 2× eq=0.
9. Понятие об угловых коэффициентах и их свойства

Рассмотрим две серые диффузные поверхности Fi и Fк и определим потоки лучистой энергии, попадающей с первой поверхности Fi на вторую Fк.
Элемент поверхности dFi излучает по всем направлениям количество энергии (собственное излучение)
dQdi = dFi× Ci× ( Ti / 100 )4. (14)
Найдем количество энергии, падающее на элемент dFк поверхности Fк. Всоответствии с определением яркости «В» это количество
d2Qdi dк = dFi× Bi× cosq i× dw (15)
где q i - угол между нормалью к элементу dFi - и прямой, соединяющей оба элемента;
|
|
|
dw - элемент телесного угла, под которым видна элементарная площадка dFк с места расположения dFi.
Величина dw по определению равна
dw = dFк× cosqк / R2, (16)
где R - расстояние между элементами dF i и dFк;
qк - угол между нормалью к элементу dFк и прямой, соединяющей оба элемента.
Подставляя dw из уравнения (16 ) в уравнение (15) и заменяя В i ( яркость собственного излучения ) на
В i =  получаем
получаем
d2Q di, dк = (17)
угловым коэффициентом излучения называется отношение лучистого потока от поверхности (или элемента) одного тела на поверхность (или элемент) другого тела к полному потоку собственного излучения, выходящего со всей поверхности (или элемента) первого тела по всевозможным направлениям в пределах полусферического телесного угла.
Этот коэффициент обозначается буквой j с двумя нижними индексами, из которых первым обозначают излучающую поверхность, а вторым - облучаемую.
Угловые коэффициенты на бесконечно малые элементы называются элементарными и обозначаются dj.
В соответствии с этим определением угловой коэффициент с dFi на dFк найдем, разделив уравнение (17) на излучение поверхности во всех направлениях (14)
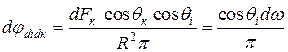
Количество энергии, которое получает вся поверхность Fк от элемента dFi определяется интегрированием уравнения (17) по Fк
 ( 18)
( 18)
При интегрировании яркость излучения вынесена за интеграл, т. к. мы считаем её независимой от направления ( излучение изотропно ).
Согласно определению угловой коэффициент с dFi на Fк найдем, разделив уравнение (18) на уравнение (14).
 (19)
(19)
локальным угловым коэффициентом излучения называется угловой коэффициент от элементарной площадки dFi на конечную поверхность Fк
|
|
|


