q = - ( l / d )×( t2 - t1 ) = ( l / d )×( t1 - t2 ) = ( l / d )×Dt (3)
¶Т / ¶t = 0.
Такое состояние температур в теле называется стационарным и зависит только от координат Т = ¦( х, у, z ).
2. При нагревании или охлаждении тела температура в каждой точке непрерывно меняется во времени. В неравномерно нагретом теле, когда оно хорошо теплоизолировано, начинается процесс выравнивания температур. Такое состояние температур в теле называется нестационарным. Математически это записывается
¶Т / ¶t ¹ 0.
Если ¶Т / ¶t > 0 - происходит нагревание тела, если ¶Т / ¶t < 0 - охлаждение.
Таким образом, температура какой либо точки тела при нестационарном состоянии является функцией четырёх переменных Т = ¦( х, у, z, t ).
25. стационарное температурное поле
в неограниченной пластине.
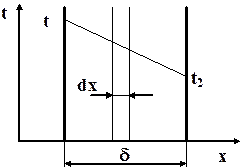
Рассмотрим пластину, размеры которой значительно превышают толщину d.
Требуется найти: распределение температуры по толщине стенки и величину теплового потока.
Известны: температуры на наружных поверхностях пластины t1 и t2, которые поддерживаются постоянными. Температура изменяется только вдоль оси х, перпендикулярно плоской стене. Коэффициент теплопроводности l - величина постоянная.
Очевидно, что для сохранения стационарного режима необходимо, чтобы количество тепла, проходящего через единицу поверхности плоскостей, были равны, в противном случае температура поверхностей должна была - бы изменяться во времени.
Выделим внутри стенки слой толщиной dх, ограниченный изотермическими поверхностями. На основании закона Фурье для этого слоя можно записать
 q = - l×
q = - l×
Разделив переменные, получим
 dt = - × dx.
dt = - × dx.
После интегрирования получим
 t = - × х + с. (1)
t = - × х + с. (1)
Постоянная интегрирования С определяется из условий на границах стенки, а именно: при х = 0; t = t1.
Подставляя это значение в уравнение (1) получаем С = t1. (2)
При х = d t = t2, следовательно
 t2 = - × d + t1
t2 = - × d + t1.
Это уравнение позволяет определить величину теплового потока q.
q = - ( l / d )× ( t2 - t1 ) = ( l / d )× ( t1 - t2 ) = ( l / d )× Dt (3)
Необходимо отметить, что тепловой поток определяется не абсолютным значением температур, а их разностью - температурным напором Dt.
Это уравнение является расчётной формулой теплопроводности плоской стенки.
Отношение l / d называют тепловой проводимостью стенки, а её обратную величину d / l - тепловым или термическим сопротивлением стенки.
Определив по формуле (3) величину теплового потока, легко вычислить количество тепла Q переданного через плоскую стенку поверхностью F, в течение времени t
 Q = q× F× t = × ( Dt× F× t ).
Q = q× F× t = × ( Dt× F× t ).
Если в уравнение (1) подставить значение постоянной С из уравнения (2) и значение q из уравнения (3) , то получим уравнение температурной кривой
Это уравнение является уравнением прямой линии.

Следовательно,
внутри однородной стенки, при постоянном значении коэффициента теплопроводности, температура изменяется по закону прямой.
26. СТАЦИОНАРНОЕ ТЕМПЕРАТРНОЕ ПОЛЕ
В МНОГОСЛОЙНОЙ ПЛАСТИНЕ
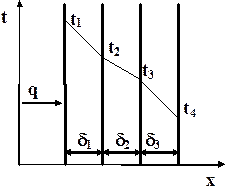
Рассмотрим стенку, состоящую из нескольких, например 3 слоёв прилегающих друг к другу с идеальным термическим контактом, так, что температуры соприкасающихся поверхностей одинаковы и неизвестны.
Температуры t1 и t4 постоянны и известны. Толщины слоев и коэффициенты теплопроводности известны.
Требуется определить: тепловой поток и температуры в стенке.
При стационарном режиме тепловой поток постоянен и для всех слоёв одинаков. Поэтому на основании формулы
(3) можно записать
 q =
q =

q =
 q =
q =
Из этих уравнений легко определить изменение температуры в каждом слое


 t1 - t2 = q×
t1 - t2 = q× 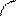
 t2 - t3 = q×
t2 - t3 = q×
 t3 - t4 = q×
t3 - t4 = q×
Суммы изменений температуры в каждом слое составляет полный температурный напор. Складывая правые и левые части системы уравнений (4) получаем


 t1 - t4 = q× ( ).
t1 - t4 = q× ( ).
Из этого соотношения определяем значение теплового потока



 q =
q =
По аналогии можно записать расчётную формулу для n -слойной пластины.

 q = .
q = .
Так как каждое слагаемое знаменателя в уравнении (5) представляет собой термическое сопротивление слоя, то из уравнения следует, что общее термическое сопротивление пластины равно сумме частных термических сопротивлений.
Если значение теплового потока из уравнения (5) подставить в уравнение (4), то получим значения неизвестных температур t2 и t3.
 t2 = t1 - q×
t2 = t1 - q×


 t3 = t2 - q× = t1 - q× ( + );
t3 = t2 - q× = t1 - q× ( + );
или
 t3 = t4 + q×
t3 = t4 + q×
Воспользуйтесь поиском по сайту:


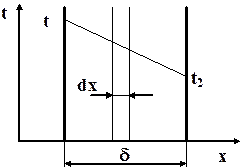
 q = - l×
q = - l×
 dt = - × dx.
dt = - × dx.
 t = - × х + с. (1)
t = - × х + с. (1) 
 Q = q× F× t =
Q = q× F× t = 
 q =
q =





 t1 - t2 = q×
t1 - t2 = q× 









 q =
q =









