Внутри каждого слоя температура изменяется по прямой, но для многослойной пластины в целом она представляет собой ломаную линию.
Внутри каждого слоя температура изменяется по прямой, но для многослойной пластины в целом она представляет собой ломаную линию.
27. ТЕПЛОПРОВОДНОСТЬ ОДНОСЛОЙНОЙ
ЦИЛИНДРИЧЕСКОЙ СТЕНКИ
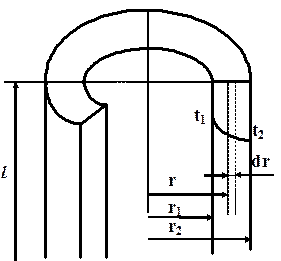
Рассмотрим полый цилиндр большой длины l c внутренним радиусом r1 и внешним радиусом r2. Коэффициент теплопроводности материала постоянен. Внутренняя и внешняя температура поверхности постоянны и равны t1 и t2, причём t1 > t2. Температура изменяется только в радиальном направлении, т. е. температурное поле является одномерным.
Требуется найти распределение температур в стенке и тепловой поток.
Выделим внутри стенки кольцевой слой толщиной dr.
Согласно закону Фурье количество тепла проходящего через этот слой в единицу времени

 Q = - l× F× = - l× 2× p× r× l×
Q = - l× F× = - l× 2× p× r× l×
Разделив переменные, получим


= -
×
Интегрирование этого уравнения даёт
 t = - × + C (6)
t = - × + C (6)
Подставляя значения переменных на границах стенки при r = r1; t = t1 и при r = r2; t = t2 получим равенство
 t1 = - × + C. (7)
t2 = - × + C. (8)
t1 = - × + C. (7)
t2 = - × + C. (8)
Вычитая из равенства (7) равенство (8) находим


 t1 - t2 = × ( ln r2 - ln r1 ) = × ln
t1 - t2 = × ( ln r2 - ln r1 ) = × ln
откуда определяется искомая величина Q

 Q = × ( t1 - t2 ) = × (t1 - t2 ). (9)
Q = × ( t1 - t2 ) = × (t1 - t2 ). (9)
Уравнение (9) является расчётной формулой теплопроводности цилиндрической стенки.
Если в уравнение (6) подставить значение постоянной С из уравнения (7), а значение Q из уравнения (9), то получим уравнение температурной кривой
 tx = t1 -
tx = t1 - ×
Это уравнение логарифмической кривой. Следовательно, внутри цилиндрической стенки при постоянном значении коэффициента теплопроводности температура изменяется по логарифмической кривой.
Количество тепла, проходящего через стенку, может быть отнесено либо к одному погонному метру длины трубы, либо к единице внутренней или внешней поверхности трубы.




 ql = = Вт / м. (10)
ql = = Вт / м. (10)
 q1 =
q1 = =
Вт / м2. (11)
q2 = =
Вт / м2. (12)
Так как внутренняя и внешняя поверхности цилиндра по величине различны, то получаются различными и значения тепловых потоков q1 и q2. Из формул (10), (11), (12), можно получить соотношения, связывающие между собой величины ql, q1, q2.
ql = p× d1× q1 = p× d2× q2
28. ТЕПЛОПРОВОДНОСТЬ МНОГОСЛОЙНОЙ
ЦИЛИНДРИЧЕСКОЙ СТЕНКИ

Пусть цилиндрическая стенка состоит из нескольких, например трёх слоёв, прилегающих друг к другу с идеальным термическим контактом.
Известны температуры на внутренней и внешней поверхностях цилиндра t1 и t4. Диаметры и коэффициенты теплопроводности отдельных слоёв известны.
Требуется найти: тепловой поток, проходящий через стенку и температуры на границе слоёв.
При стационарном режиме количество тепла проходящего через каждый слой, одинаково и постоянно. Поэтому на основании формулы (10) можно написать
 qℓ =
qℓ = ;
qℓ =
qℓ =
Из этих уравнений определяется изменение температуры в каждом слое.
 t1 - t2 =
t1 - t2 =
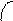
 t2 - t3
t2 - t3


 = (13)
= (13)
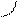 t3 - t4 =
t3 - t4 =
Сумма изменений температуры в каждом слое составляет полный температурный напор.
Складывая отдельно левые и правые части, получаем






 t1 - t4
t1 - t4 =
( + + ),



откуда определяем
значение теплового потока




 ql = . (14)
ql = . (14)
По аналогии можно написать формулу для n -слойной стенке.

 q i =
q i =
Если значение q i из формулы (14) подставить в уравнение (13), то получим значения неизвестных температур.
t2 = t1 -







 t3 = t2 - = t1 - ( ).
t3 = t2 - = t1 - ( ).



Или
t3 = t4 +
Воспользуйтесь поиском по сайту:


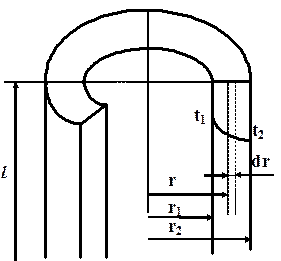

 Q = - l× F× = - l× 2× p× r× l×
Q = - l× F× = - l× 2× p× r× l×


 t = - × + C (6)
t = - × + C (6)

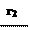

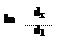
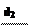










 ql = = Вт / м. (10)
ql = = Вт / м. (10)
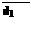

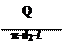


 qℓ = ;
qℓ = ;


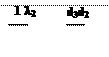



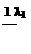

 t1 - t2 =
t1 - t2 =
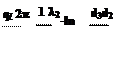
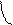

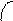
 t2 - t3
t2 - t3 

 = (13)
= (13)
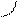 t3 - t4 =
t3 - t4 = 





 t1 - t4 = ( + + ),
t1 - t4 = ( + + ),










 q i =
q i =













