34. Граничные условия 1го рода. ТПОВ = ¦(t) илитпов = ¦(х, у, z, T). Tн - температура в начальный момент времени, 0С. T /x ± s = tп, или  (15)

34. ГРАНИЧНЫЕ УСЛОВИЯ 1ГО рода

В этом случае задаётся распределение температуры по всей поверхности тела и изменение этого распределения во времени, т. е. задаётся функция

Тпов = ¦(t) илиТпов = ¦(х, у, z, t).

В частных случаях эта температура может быть постоянна во времени, t_пов = const ( процессы нагрева или охлаждения с мгновенным изменением температуры поверхности тела, процессы выдержки ), или изменяться во времени, например, с постоянной скоростью t_пов = t_н +c× t,

где С - скорость изменения температуры поверхности тела, ⁰С / час;

tн - температура в начальный момент времени, 0С.

На практике применяется в режимах термообработки.

36. РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ ПРИ ПОСТОЯННОЙ ТЕМПЕРАТУРЕ ПОВЕРХНОСТИ ТЕЛА

Рассмотрим симметричный нагрев пластины неограниченной длины и ширины, но ограниченной толщины - 2s и цилиндра бесконечной длины радиусом  R.

Граничные условия имеют следующий вид;

t /x ± S = tп,  или                                                 (15)

t / r = R =tп,                                                       (16)

где t_п = const.

Рассмотрим варианты начальных условий

1. На поверхности тела с одинаковой температурой по толщине, температура поверхности мгновенно изменяется до заданного значения и затем в процессе нагрева (охлаждения) поддерживается постоянной.

Начальные условия имеют следующий вид:

t /t=0 = tн.                                       (17)

Графическое представление краевых условий.

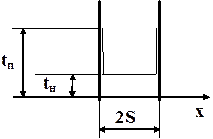
Температура поверхности тела может мгновенно принять температуру окружающей среды при условии, что коэффициент теплоотдачи a будет очень большим, т. е. стремиться к ¥,   следовательно, и интенсивность внешнего теплообмена будет настолько велика, что поверхность тела мгновенно примем температуру окружающей среды

В результате заданной величиной оказывается температура поверхности тела, т. е. получаются граничные условия первого рода.

Следовательно, критерий Био не является более параметром задачи. Лимитирующим звеном в процессе нагрева или охлаждения является внутренний теплообмен

Подставляя (15) и (17) в общее решение уравнения теплопроводности (при граничных условиях первого рода) и произведя интегрирование и преобразование, получим решение для бесконечной пластины

 

t = tп + ( tн - tп )×           (18)

	2l - 1

p

где d_l =                    - ( имеет смысл центрального угла выраженного в радианах );

l = 1; 2; 3; ^... - нормальный ряд чисел.

В этом решении сумма бесконечного ряда может быть выражена как функция двух безразмерных параметров: величины критерия Фурье содержащего время t и симплекса х / s содержащего координату х

а× t

Если в выражение (18)  перенесём температуры в левую часть, то решение можно представить в общем виде

	tп - t
			Fплл пл

tп - tн

s2

=

                    (           ; х / s ).

 

Значения F_пл вычислены и представлены в виде графиков.

 

tп - t

tп - tн

               = q - безразмерная температура

 

Решение для бесконечного цилиндра получим после подстановки граничных (16) и начальных (17) условий в общее решение уравнения теплопроводности

t = tп + ( tн - tп )×       (19)

 

i₀  и I₁ - функции Бесселя нулевого и 1^го порядка.

m× I1(m)

m_n - значение корней трансцендентного уравнения Bi =

 

I0(m)

Решение в критериальной форме будет иметь вид

q_ц = F_ц( Fo; X ),

где  X = r / R.

Значения функции F_ц представлены в литературе в виде графиков.

Если расчёт ведётся для установления температуры центра изделия, т. е. х / s = 0; r / R = 0, то расчётные уравнения примут вид:

	а

S2

× t

для пластины q_пл = F_пл^с (     )

 

 

а

R2

× t

для цилиндра q_ц = F_ц^с (     ).

Значения функций F_пл^с  и F_ц^с  также приведены в литературе. Есть в литературе и данные для различных значений х / s и r / R.

Для бесконечной пластины температура в середине тела в момент времени t  может быть найдена по формуле ( при  а× t / S² ³ 0, 06 )

 

tп - t

tп - tн

= 1, 27

 

Для цилиндра бесконечной длины температура на оси может быть рассчитана по формуле ( при  а× t / R² ³ 0, 08 )

 

tп - t

tп - tн

= 1, 61

 

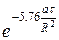
Рассмотренные граничные условия 1^го  рода осуществляются на практике при очень большой интенсивности внешнего теплообмена.

Например, при закалке в жидкостях, температура кипения которых ниже температуры нагрева под закалку. Или при нагреве в жидких металлах и соляных ваннах.

Коэффициент теплоотдачи от изделия к жидкости имеет порядок 

a » 10³ ¸ 10⁴ Вт / м²× К

⇐ Предыдущая15161718192021222324Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: