Результатом решения дифференциального уравнения (его интегралом) является уравнение температурного поля в теле Т = ¦(х, у, z, t).

Результатом решения дифференциального уравнения (его интегралом) является уравнение температурного поля в теле Т = ¦(х, у, z, t).

Так как форма тел и условия их нагрева бесконечно разнообразны, то, следовательно, бесконечно разнообразны и решения дифференциального уравнения. Чтобы получить однозначное решение необходимо математически описать конкретный случай нагрева т. е. сформулировать условия однозначности.

В условия однозначности входят: геометрические условия, определяющие форму и размеры тела; физические параметры материала, т. е. l, r, с; начальные условия, характеризующие распределение температур в объёме тела в момент времени, принимаемый за начало нагрева или охлаждения; граничные условия, характеризующие тепловое взаимодействие окружающей среды с поверхностью тела, или показывающие изменение температуры на поверхности тела.

Граничные условия можно сформулировать тремя различными способами. Целесообразность того или другого способа определяется конкретными условиями нагрева или охлаждения.

 

31. ОБЩЕЕ РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ

В результате решения уравнения теплопроводности была найдена такая функция, которая одновременно удовлетворяла уравнению и краевым условиям.

Полученная функция зависит от большого числа параметров, однако, анализ решения позволил сгруппировать эти величины в два безразмерных комплекса. Эти комплексы являются критериями подобия

 

Вi = a× s / l;         Fo = а× t / s²

На основании второй теоремы подобия ( зависимость между переменными, характеризующими какой - либо процесс, может быть представлена в виде зависимости между критериями подобия ) искомая функция

	tпов - t

tпов - tн

Q =                   в различных сходственных точках Х = х / s  или   X = r / R

может быть представлена в виде зависимости между критериями подобия

q= ¦( Вi; Fo; Х ).

 

32. Физический смысл критерия Фурье

Критерий Фурье Fo = а× t / s² характеризует связь между временем прогрева системы, физическими свойствами и размерами тела, являясь мерой отношения теплового потока и скорости аккумуляции тепла, поступившего в систему.

Эта связь ясна из следующей модификации критерия Фурье: если умножить числитель и знаменатель на   S²,   то после перегруппировки критерий получает вид

			l× t× s2 s
					1 cp× r× s3

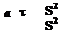Fo =            =

×

s2

 

l× t× s2 s

где              - представляет количество тепла, поступившего за счёт теп-

cp× r× s3

лопроводности за время  t;

 - аккумулированное тепло.

Иначе говоря, критерий Фурье оценивает скорость изменения температуры тела при нестационарном поле

Из структуры Fo   можно заключить, что при его неизменной величине время для нагрева или охлаждения зависит от линейных размеров тела 

t = Fo× s2/а     и пропорционально s2.

33. ФИЗИЧЕСКИЙ СМЫСЛ КРИТЕРИЯ БИО

Критерий Био Вi = a× s / l по своей структуре напоминает критерий Нуссельта, но является определяющим критерием, т. к. в него входят условия однозначности ( коэффициент теплоотдачи задается ).

Критерий Вi  по физическому смыслу представляет меру отношения теп л ового сопротивления твёрдого тела s / l и теплового сопротивления 1 / a теплоотдачи в окружающую среду, что видно из его структуры

 

1 / α

s / l

Вi =         ^.

Или, критерий Био является мерой относительной интенсивности переноса тепла от омывающей среды на поверхности тела к переносу тепла в самом теле.

⇐ Предыдущая14151617181920212223Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: