 |
Основы финансовой математики.
|
|
|
|
Задача 10.1.3.1
В долг на 12 месяцев предоставлена сумма в 20 тыс.руб. с условием возврата 25 тыс.руб. Определить доходность операции.
Решение:
Выданная сумма составляет первоначальный капитал (Р=20тыс.руб.), возвращаемая сумма составляет наращенный капитал (F=25 тыс.руб.), срок операции n=12мес.=1 год. Доходность операции характеризуется процентной и учетной ставками, которые могут быть получены методами простых и сложных процентов, следовательно, требуется получить четыре варианта значений.
Простая процентная ставка 
Простая дисконтная ставка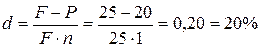 
Сложная процентная ставка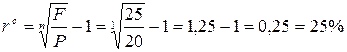 
Сложная дисконтная ставка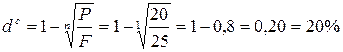 
Таким образом, чтобы получить эквивалентный доход, следует применить простую и сложную процентную ставку в размере 25% или простую и сложную дисконтную ставку в размере 20% годовых.
Задача 10.1.3.2.
Оцените, что лучше: получить 20 тыс.руб. через 3 года или 25 тыс.руб. через 6 лет, если можно поместить деньги на депозит под сложную процентную ставку 10% годовых.
Решение:
Так как периоды времени получения денежных сумм различны (n1=3года, n2=6лет), для сопоставимости данных следует привести данные суммы по стоимости к текущему моменту времени, используя процедуру дисконтирования, т.е. найти современную стоимость 20 и 20 тыс.руб., учитывая, что доходность начисляется по схеме сложных процентов.
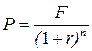
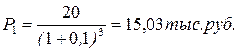
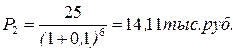
Так как Р1>Р2, то выгоднее получить 20тыс.руб. через 3 года, чем 25 тыс.руб. через 6 лет.
Задача 10.1.3.3
Предполагаемый ежегодный доход от реализации проекта составит в первые три года 10 млн.руб., а последующие два года – 15 млн.руб.
Какова стоимость проекта в современном масштабе цен, если ставка процента в первые два года составляет 15%, а затем 10% годовых.
|
|
|
Решение:
Так как предполагается ежегодное получение дохода, речь идет о денежном потоке, члены которого равны:
Р1=Р2=Р3=10, Р4=Р5=15 тыс.руб.
Ставка доходности при этом в течение срока финансовой операции (n=5лет) будут изменены, т.е.:
r1=r2=15%=0,15, r3=r4=r5=10%=0,1
Современная стоимость потока платежей по простым процентам определяется как:
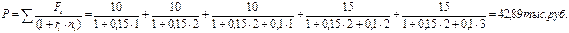
Современная стоимость потока платежей по сложным процентам:
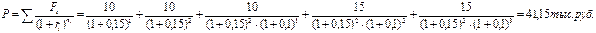
Задача 10.1.3.4
От эксплуатации автомобиля предприятие может получать в течение 3 лет доход в размере 10 тыс.руб. в год. Определите, какую минимальную сумму должно получить предприятие, чтобы в случае вложения выручки в банк под 10% годовых на 3 года, иметь тот же результат, что и от эксплуатации машины. Остаточная стоимость автомобиля через 3 года – 20 тыс.руб.
Решение:
Задача предусматривает эквивалентность двух вариантов – доход от эксплуатации автомобиля и доход от размещения выручки от продажи автомобиля должны быть равны.
Определяем сумму, которую получит владелец за три года, если оставит автомобиль в эксплуатации:
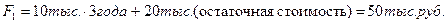
согласно принципу эквивалентности дохода первого и второго варианта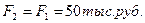 
, откуда
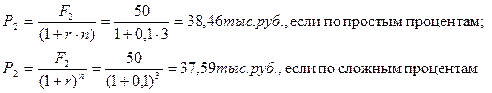
Таким образом, чтобы от продажи автомобиля получить такой же доход как и от его эксплуатации, его следует продать за 38,46 тыс.руб., если банк предлагает простые проценты или за 37,59тыс.руб., если банк предлагает сложные проценты.
Задача 10.1.3.5
В страховой фонд производятся взносы в течение 3 лет, ежегодно по 1000 руб., на которые начисляются проценты по сложной ставке 12% годовых. Рассчитайте наращенную сумму при условии, что взносы вносятся: а) в конце года, б) в начале года.
Решение:
Так как взносы вносятся ежегодно и представляют собой однонаправленные платежи, то речь идет о годовой финансовой ренте с ежегодным начислением процентов по варианту а) постнумерандо, по варианту б) пренумерандо.
Наращенная стоимость годовой ренты постнумерандо:
|
|
|
,
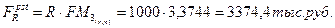где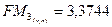 
согласно таблицы коэффициентов наращения аннуитета.
Наращенная стоимость годовой ренты пренумерандо:
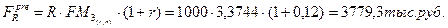
Задача 10.1.3.6
Проект, рассчитанный на 15 лет, требует инвестиций в размере 150000 ден.ед. В первые 5 лет никаких поступлений не ожидается, однако, в последующие 10 лет ежегодный доход составит 50000 ден.ед. Следует ли принять этот проект, если доходность активов составляет 10% в год.
Решение:
Чтобы ответить на вопрос задачи следует сравнить сумму предполагаемого вложения и сумму, которую получит владелец первоначального капитала от инвестирования средств. Для этого необходимо получить современную стоимость инвестиционного дохода. Так как предполагается ежегодное получение дохода в течение 10 лет, то в начале найдем современную стоимость ренты на конец пятого года:
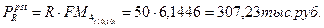
Далее находим современную стоимость полученного результата на начало первого года:
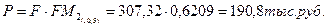
Таким образом, современная стоимость инвестиционного дохода составит 190,8 тыс.руб., что больше предполагаемой суммы вложений (150тыс.руб.), следовательно, проект можно принять.
Задача может быть решена и другим способом:
Оцениваем наращенную стоимость первоначального капитала, учитывая, что стоимость активов 10%, т.е. у владельца есть альтернативная возможность для размещения капитала:
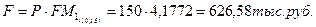
Тогда наращенная стоимость инвестиционного дохода к концу 15-го года составит:
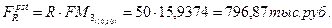
Таким образом, доход от инвестиционного проекта выше, чем доход, полученный от альтернативного размещения первоначального капитала, следовательно проект можно принять.
Задача 10.1.3.7
Фирма вкладывает по 1 млн.ден.ед. ежегодно в конце периода в течение 5 лет под 10% годовых. На какую сумму следует ежегодно увеличивать платеж, чтобы получить эквивалентный доход за тот же период, если первоначальный платеж составит 0,5 млн.ден.ед. при неизменной доходности.
Решение:
Так как по второму варианту необходимо получить доход, эквивалентный первоначальному варианту, определяем наращенную стоимость годовой ренты постнумерандо:
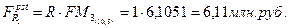
Откуда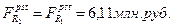 
Второй вариант предусматривает ренту с изменяющимися членами при R=0,5млн.руб. Так как известна наращенная стоимость, то величину приращения члена ренты находим из формулы наращенной стоимости ренты постнумерандо с изменяющимися членами:
|
|
|
,
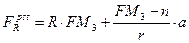откуда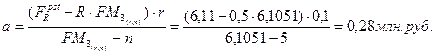 
Таким образом, можно получить одинаковый результат, если вкладывать 1млн.руб. в течение 5 лет или вложив первоначально 0,5млн.руб. увеличивать ежегодно платеж на 0,28 млн.руб.
Задача 10.1.3.8
В банк на три года положено 1000 руб. под 12% годовых при ежемесячном начислении процентов. Определите, какой должна быть простая процентная ставка, чтобы при прочих равных условиях обеспечить эквивалентный исходным условиям доход.
По условию следует найти эквивалентную простую процентную ставку при внутригодовом начислении процентов:
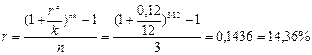
Таким образом, чтобы получить такой же доход, что и при исходных условиях, следует применить простую процентную ставку в размере 14,36%.
Задача 10.1.3.9
Вклад в размере 20 тыс.руб. помещен в банк сроком на 5 лет при начислении сложных процентов: в первые два года – 16%, в последующие два года – 10%, в оставшийся год – 23%. Найдите наращенную сумму. При использовании какой постоянной а) сложной, б) простой процентной ставки можно получить такую же наращенную сумму?
Исходная формула 
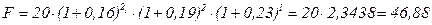тыс.руб.
Для определения постоянной ставки сложного процента используем формулу
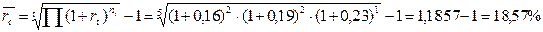
Следовательно, чтобы получить эквивалентный результат, можно использовать постоянную ставку в размере 18,57%.
|
|
|
