 |
Лекция 3. Теория сложного напряженно-деформированного состояния (НДС) твердого тела
|
|
|
|
Напряжённое и деформированное состояние частицы тела
Теория НДС ставит своей задачей определение внутренних напряжений, деформаций и перемещений в различных точках деформируемого твёрдого тела произвольной формы и размеров.
Напряженным состоянием тела в точке называют совокупность нормальных и касательных напряжений, действующих по всем площадкам (сечениям), содержащим данную точку.
Отнесём тело к координатным осям x, y, z и выделим мысленно из него материальную частицу в виде параллелепипеда или кубика размерами dx, dy, dz (рис. 3.1)
А) б)
Рис. 3.1
Действия отброшенной части тела заменим векторами – напряжениями 
и разложим их на составляющие по координатным осям.
(1)
где ex, ey, ez - единичные векторы, направленные вдоль координатных осей x, y, z; 
, 
, 
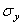- нормальные напряжения, 
, 
, 
, 
, - касательные напряжения. У касательных напряжений первый индекс указывает на направление его действия, второй индекс – на нормаль к площадке, на которой оно действует. У нормальных напряжений индекс соответствует одновременно как направлению, так и нормали к площадке их действия. На невидимых на рис. 3.1 гранях частицы действуют такие же, но противоположно направленные напряжения.
Совокупность указанных напряжений полностью характеризует напряжённое состояние частицы тела. Эту совокупность записывают в виде квадратной матрицы
(2)
и называют тензором напряжений Коши. Система напряжений, приложенных к частице тела, должна удовлетворять условиям равновесия. Первые три условия в проекциях на оси x, y, z дают тождества, т.к. на противоположных гранях мы считаем напряжения равными по величине. Остаётся проверить, обращаются ли в нуль суммы моментов всех сил относительно координатных осей. Составим условие равновесия моментов относительно оси х:
|
|
|
откуда следует 
Аналогично можно составить два уравнения равновесия моментов относительно осей y и z. В результате получим соотношения:
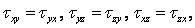(3)
которые называют законом парности касательных напряжений: на двух взаимно перепендикулярных площадках составляющие касательных напряжений, ортогональные их общему ребру, равны по величине и направлены оба либо к ребру, либо от него. На основании этого закона тензор-матрица напряжений 
является симметричной относительно главной диагонали, состоящей из нормальных напряжений.
Напряжение
(4)
называют средним напряжением. Тензор напряжений, для которого 
, называется тензором–девиатором напряжений. В общем случае тензор напряжений можно разложить на сумму двух тензоров:
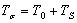
Первый из них
(5)
носит название шарового тензора напряжений, а второй:
(6)
тензора–девиатора или просто девиатора напряжений.
Иногда компоненты девиатора напряжений обозначают:
Шаровой тензор характеризует напряженное состояние всестороннего растяжения – сжатия частицы тела, а девиатор – напряженное состояние её формоизменения.
На каждую частицу тела кроме напряжений действуют объёмные силы:
,
где Rx, Ry, Rz – проекции этих сил на координатные оси. Каждая вектор-сила 
действует на единицу объёма.
На поверхности тела F на каждую единицу её площади могут действовать распределённые силы:
,
где qx, qy, qz – проекции этих сил.
Если последние действуют на малых площадках контакта 
поверхности тела, то их, согласно принципу смягчения граничных условий Сен-Венана, заменяют главными вектором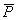 
и моментом 
всех сил, действующих на этих малых площадках:
где 
- радиус – вектор, проведённый из заданной точки (центра приведения сил) на до текущей силы 
.
|
|
|
В результате действия на тело внешних сил , температуры Т каждая точка В совершает перемещение 
в новое положение В ’. Это перемещение характеризуется направленным отрезком 
, т.е. вектором перемещения:
,
где u, v, w – проекции этого перемещения на координатные оси.
Перемещения характеризуют деформацию тела в целом. Например, прогибы точек оси балки V и поворот поперечных сечений, проходящих через эти же точки, характеризуют деформацию балки в целом при её изгибе.
Деформация тела складывается из деформации её материальных (физических) частиц, каждая из которых испытывает удлинения 
в направлении её рёбер и искажения прямых углов:
между её гранями в каждой из координатных плоскостей (рис. 3.2).
Величины
называют относительными удлинениями или деформациями частиц тела. Половины сдвигов обозначают:
.
Совокупность шести компонентов деформации полностью характеризует деформированное состояние частицы тела. Эту совокупность запишем в виде квадратной матрицы:
(7)
и назовем тензором деформаций Коши.
А) б)
Рис. 3.2
Величину
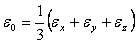(8)
называют средней деформацией.
Если для рассматриваемого тензора деформация 
, то он называется тензором-девиатором или просто девиатором деформации.
В общем случае 
тензор (7) можно разложить на сумму двух тензоров:
Первый из них:
(9)
носит название шарового тензора деформации и описывает объёмную деформацию всестороннего растяжения – сжатия.
Второй тензор:
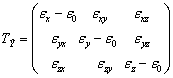(10)
представляет собой тензор-девиатор и характеризует деформацию изменения формы частиц тела.
|
|
|
