Расчеты на прочность и жесткость валов круглого и кольцевого сечений

При расчетах на прочность при кручении (также как и при растяжении) могут решаться три задачи:

а) проверочный расчет – проверить, выдержит ли вал приложенную нагрузку;

б) проектировочный расчет - определить размеры вала из условия его проч­ности;

в) расчет по несущей способности - определить максимально допустимый крутящий момент.

- При проверочном расчете на прочность рекомендуется следующий порядок расчета валов при кручении:

1) по схеме вала и действующим на него скручивающим моментам строят эпюру внутренних крутящих моментов по отдельным участкам;

2) выбирают материал для рассчитываемого вала и определяют для этого ма­териала допускаемое напряжение, например по формуле (5.9), ;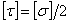

3) для участка вала с максимальным по модулю значением крутящего момента записывают условие прочности при кручении

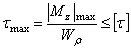
- Проектировочный расчет проводится, исходя из условия прочности на основе следующего соотношения:

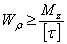
Для сплошного круглого сечения 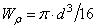, отсюда можем записать вы­ражение для определения диаметра вала из условия его прочности:

Для кольцевого сечения

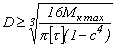
Определив размеры вала из условия прочности, проверяют вал на жесткость.

Условие жесткости требует, чтобы максимальный относительный угол закручивания 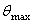, был меньше или в предельном случае равен допускаемому углу закручивания единицы длины вала, т.е.

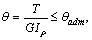
. (5.11)

Из условия прочности можно найти необходимый для обеспечения прочности полярный момент сопротивления сечения, а по нему и диаметр вала:

но W_ρ = 0,2 d³, поэтому

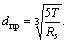(5.12)

Из формулы (5.11) можно найти необходимый полярный момент инерции сечения, а по нему и диаметр вала

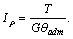
В этой формуле допускаемый относительный угол закручивания 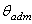должен быть выражен в радианах; если этот угол дан в градусах, то соотношение для определения I_p будет выглядеть следующим образом:

но I_p = 0,1 d ⁴ , поэтому

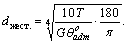(5.13)

Из двух диаметров, рассчитанных по формулам (5.12) и (5.13), в качестве окончательного диаметра выбирается больший, который обычно округляется до целых миллиметров.

В случае расчета размеров вала кольцевого поперечного сечения при заданном соотношении внутреннего d _вн и наружного диаметров d, т.е. при заданном параметре k = d _вн /d, формулы (5.12) и (5.13) принимают вид:

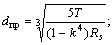(5.14)

(5.15)

 

Пример 2.

Подобрать диаметр сплошного вала, передающего мощность N =450 л.с. при частоте вращения n =300 об/мин. Угол закручивания не должен превышать одного градуса на 2 метра длины вала; =40 МПа, G =8 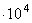МПа.

Решение.

Крутящий момент определяем из уравнения

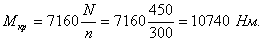
Диаметр вала по условию прочности определяется из уравнения

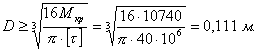
Диаметр вала по условию жесткости определяется из уравнения

Выбираем больший размер 0,112 м.

 

Пример 4.

Найти мощность в квт, передаваемую валом, если диаметр сплошного вала 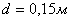, число оборотов вала в минуту 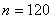, модуль сдвига 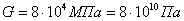и угол закручивания участка вала длиной 7,5 м равен 1/15 ра­диан.

Решение.

Из формулы

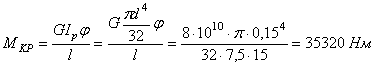
Определим передаваемую мощность

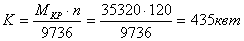
Пример 7.

К стальному валу (см.рис.5.10) приложены скручивающие моменты: М₁, M₂, M₃, M₄. Требуется:

1) построить эпюру крутящих моментов;

2) при заданном значении определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей, соответственно равной: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм;

3) построить эпюру углов закручивания;

4) найти наибольший относительный угол закручивания.

Дано: М ₁ = М ₃ = 2 кНм, М ₂ = М ₄ = 1,6 кНм, а = b = с = 1,2 м, = 80 МПа.

Рис.5.10

 

Решение.

1. Построить эпюру крутящих моментов.

При построений эпюр М _кр примем следующее правило знаков: крутящий момент считается положительным, если при взгляде в торец отсеченной части бруса действующий на него момент представляется направленным по движению часовой стрелки.

Крутящие моменты, возникающие в поперечных сечениях брусьев, определяются по внешним окручивающим моментам с помощью метода сечений. На основании метода сечения крутящий момент в произвольном поперечном сечении бруса численно равен алгебраической сумме внешних скручивающих моментов, приложенных к брусу по одну сторону от рассматриваемого сечения.

Для брусьев, имеющих один неподвижно закрепленный (заделанный) и один свободный конец, крутящие моменты всех поперечных сечений удобно выражать через внешние моменты, приложенные с той стороны от рассматриваемого сечения, с которой расположен свободный конец. Это позволяет определять крутящие моменты, не вычисляя реактивного момента, возникающего в заделке.

Для построения эпюры крутящих моментов необходимо найти величины крутящих моментов на каждом участке вала.

I участок (КД):

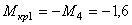кНм,

II участок (СД):

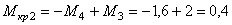кНм,

III участок (СВ):

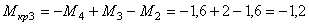кНм,

IV участок (ВА):

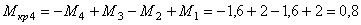кНм.

По значению этих моментов строим эпюру М _кр в выбранном масштабе. Положительные значения М _кр откладываем вверх, отрицательные - вниз от нулевой линии эпюры (см. рис.5.11).

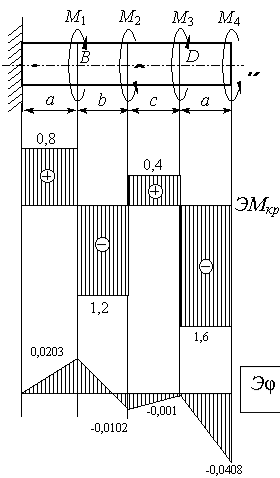
Рис.5.11

 

2. При заданном значении определим диаметр вала из расчета на прочность.

Условие прочности при кручении имеет вид

.

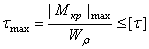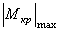- максимальный крутящий момент, взятый по абсолютной величине. Определяется из эпюры М _кр (рис.5.11).

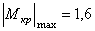кНм;

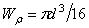- полярный момент сопротивления для сплошного круглого вала.

Диаметр вала определяется по формуле

.

Принимаем d = 50 мм = 0,05 м.

3. Построим эпюру углов закручивания.

Угол закручивания участка вала длиной l постоянного поперечного сечения определяется по формуле

.

где 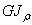- жесткость сечения вала при кручении.

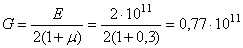Н/м²;

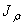- полярный момент инерции круглого вала

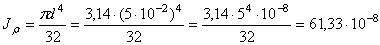м⁴.

Вычислим углы закручивания сечений В, С, D и К относительно закрепленного конца вала (сечения А)

рад,

рад,

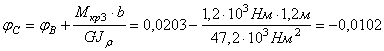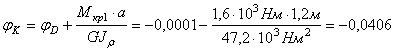рад,

рад.

Строим эпюру углов закручивания (рис.5.11).

4. Найдем наибольший относительный угол закручивания

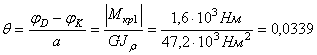рад/м.

 

Сдвиг

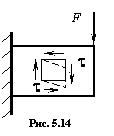
Сдвигом называют деформацию, представляющую собой искажение первоначально прямого угла малого элемента бруса (рис.5.14) под действием касательных напряжений . Развитие этой деформации приводит к разрушению, называемому срезом или, применительно к древесине, скалыванием. Примером сдвига является резка полосы ножницами. На сдвиг работают жесткие соединения конструкций – сварные, заклепочные и так далее.

 

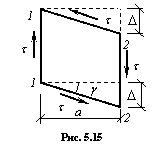
Деформация сдвига оценивается взаимным смещением граней 1 – 1 и 2 – 2 малого элемента (рис. 5.15), называемым абсолютным сдвигом и более полно – относительным сдвигом (углом сдвига)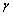

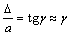, (5.19)

являющимся безразмерной величиной.

 

В предположении равномерного распределения касательных напряжений по сечению площадью А, они определяются по формуле

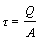, (5.20)

где Q – поперечная сила в данном сечении.

Условие прочности записывается по минимальной площади среза S _min, отражающей минимальное число соединяющих элементов (заклепок, болтов, штифтов и т.д.) или минимальную длину сварного шва.

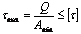
Величина допускаемых напряжений 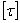зависит от свойств материала, характера нагрузки и может быть определена по 3-ей теории прочности: , а так как при чистом сдвиге 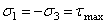, то

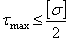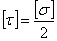, (5.21)

При расчете болтовых или заклепочных соединений учитывается смятие контактирующих поверхностей, то есть пластическую деформацию, возникающую на поверхности контакта.

,

где A_см – площадь проекции поверхности контакта на диаметральную плоскость.

При выполнении проектного расчета, то есть при определении необходимого диаметра заклепки, болта или при определении их количества необходимо учитывать условие прочности на срез и на смятие, из двух значений следует взять большее число, округлив его до ближайшего целого в меньшую сторону.

Примечания: 1. Так как болты и заклепки ослабляют соединяемые листы, последние проверяют на разрыв в ослабленных сечениях

.

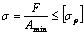При расчетах сварных швов наплывы не учитывают, а считают, что в разрезе угловой шов имеет форму прямоугольного равнобедренного треугольника и разрушение шва происходит по его минимальному сечению, высота которого

,

где 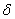– минимальная толщина соединяемых листов.

В пределах упругости касательное напряжение прямо пропорционально относительному сдвигу

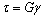(5.22)

– это закон Гука при сдвиге; G – модуль сдвига, Н/м², характеризующий жесткость материала при сдвиге.

Закон Гука при сдвиге через абсолютные деформации:

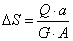, (5.23)

где а – расстояние между сдвигаемыми гранями; А – площадь грани.

Модуль сдвига G, модуль продольной упругости Е и коэффициент Пуассона 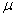материала связаны зависимостью

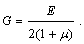
Удельная потенциальная энергия деформации сдвига равна

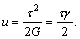
На практике чаще всего теория сдвига применяется к расчету болтов, заклепок, шпонок, сварных швов и других элементов соединений.

Расчет заклепок на срез

Мы изучали, что при простом растяжении или простом сжатии две части стержня, разделенные наклонным сечением, стремятся не только оторваться друг от друга, но и сдвинуться одна относительно другой. Растяжению сопротивляются нормальные, а сдвигу — касательные напряжения.

На практике целый ряд деталей и элементов конструкций работает в таких условиях, что внешние силы стремятся их разрушить именно путем сдвига.

В соответствии с этим при проверке прочности таких элементов на первый план выступают касательные напряжения. Простейшими примерами подобных деталей являются болтовые и заклепочные соединения. Заклепки во многих случаях уже вытеснены сваркой; однако они имеют еще очень большое применение для соединения частей всякого рода металлических конструкций: стропил, ферм мостов, кранов, для соединения листов в котлах, судах, резервуарах и т. п. Для образования заклепочного соединения в обоих листах просверливают или продавливают отверстия. В них закладывается нагретый до красного каления стержень заклепки с одной головкой; другой конец заклепки расклепывается ударами специального молотка или давлением гидравлического пресса (клепальной машины) для образования второй головки. Мелкие заклепки (малого диаметра — меньше 8 мм) ставятся в холодном состоянии (авиационные конструкции).

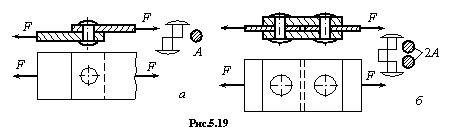
Для изучения работы заклепок рассмотрим простейший пример заклепочного соединения (рис.5.16). Шесть заклепок, расположенных в два ряда, соединяют два листа внахлестку. Под действием сил Р эти листы стремятся сдвинуться один по другому, чему препятствуют заклепки, на которые и будет передаваться действие сил P).

 

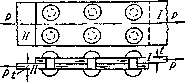
Рис.5.16.

 

Для проверки прочности заклепок применим общий порядок решения задач сопротивления материалов.

На каждую заклепку передаются по две равные и прямо противоположные силы: одна—от первого листа, другая — от второго. Опытные исследования показывают, что одни из заклепок ряда нагружаются больше, другие — меньше. Однако к моменту разрушения усилия, передающиеся на различные заклепки, более или менее выравниваются за счет пластических деформаций. Поэтому принято считать, что все заклепки работают одинаково. Таким образом, при заклепках в соединении, изображенном на рис.5.16, на каждую из них действуют по две равные и противоположные силы 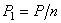(рис.5.17); эти силы передаются на заклепку путем нажима соответствующего листа на боковую полуцилиндрическую поверхность стержня. Силы стремятся перерезать заклепку по плоскости mk раздела обоих листов.

Рис.5.17.

 

Для вычисления напряжений, действующих по этой плоскости, разделим мысленно заклепочный стержень сечением mk и отбросим нижнюю часть (рис.5.17). Внутренние усилия, передающиеся по этому сечению от нижней части на верхнюю, будут уравновешивать силу т. е. будут действовать параллельно ей в плоскости сечения, и в сумме дадут равнодействующую, равную . Следовательно, напряжения, возникающие в этом сечении и действующие касательно к плоскости сечения, это — касательные напряжения . Обычно принимают равномерное распределение этих напряжений по сечению. Тогда при диаметре заклепки d на единицу площади сечения будет приходиться напряжение:

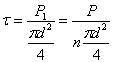
Величина допускаемого касательного напряжения , или, как говорят, допускаемого напряжения на срез, принято определять в виде: . Зная , мы напишем условие прочности заклепки на перерезывание в таком виде:

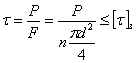
т. е. действительное касательное напряжение в материале заклепки должно быть равно допускаемому , или меньше его.

Из этого условия можно определить необходимый диаметр заклепок, если задаться их числом, и наоборот. Обычно задаются диаметром заклепочных стержней d в соответствии с толщиной t склепываемых частей (обычно ) и определяют необходимое число заклепок :

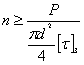
Знаменатель этой формулы представляет собой ту силу, которую безопасно может взять на себя каждая заклепка.

Пусть ; тогда

Рис.5.18

При проектировании строительных конструкций применяется следующее условие прочности на срез для заклепок и болтовых соединений

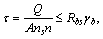(5.24)

где Q – поперечная сила, равная внешней силе F, действующей на соединение; R_bs – расчетное сопротивление на срез; 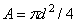– расчетная площадь сечения болта или заклепки; d – диаметр заклепки или наружный диаметр болта; n_s – число срезов одного болта или заклепки; 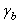– коэффициент условий работы соединения, имеющий значения в интервале 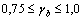; n – число болтов или заклепок.

Если величины F, R_bs, 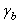, n_s известны, то задаваясь числом заклепок или болтов n, можно найти необходимый для обеспечения прочности на срез диаметр

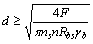. (5.25)

А зная d, F, R_bs, 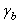, n_s, можно определить потребное число заклепок или болтов

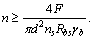(5.26)

 

Вопросы для самопроверки

- Какой вид нагружения называется кручением?

- При каком нагружении возникает кручение бруса (вала)?

- Какой силовой фактор вызывает закручивание бруса?

- Что такое крутящий момент?

- Что называется валом?

- Как называется напряженное состояние, возникающее при кручении круглого бруса (вала)?

- Какие деформации возникают при кручении?

- Какие гипотезы выполняются при деформации кручения?

- Изменяются ли длина и диаметр вала после скручивания?

- Какие внутренние силовые факторы возникают при круче­нии?

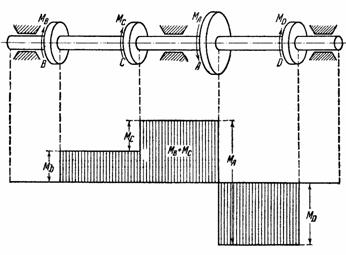
- Что такое рациональное расположение колес на валу?

- Какая теоретическая зависимость существует между внешним крутящим моментом, поступающим на вал, и передаваемой мощностью?

- Как вычисляется скручивающий момент, передаваемый шкивом, по заданной мощности и числу оборотов в минуту?

- Как вычисляют значение крутящего момента в поперечном сечении вала?

- Что такое эпюра крутящего момента и как она строится?

- Для чего строится эпюра крутящих моментов?

- Опишите технику построения эпюры крутящих моментов?

- Какие предпосылки используются в теории кручения круговых брусьев?

- Перечислите гипотезы, принимаемые в теории кручения прямого вала круглого поперечного сечения.

- Какие напряжения возникают в поперечном сечении круглого вала при кручении и как они направлены?

- По какой формуле определяется касательное напряжение при кручении?

- Напишите формулу для определения напряжений в поперечном сечении скручиваемого круглого вала.

- Получите формулу касательных напряжений при кручении кругового бруса? Охарактеризуйте эпюру напряжений? Каким выражением определяются наибольшие касательные напряжения, как записывается условие прочности при кру­чении?

- Как распределяется касательное напряжение при кручении? Чему равно напряжение в центре круглого поперечного сечения?

- Какое напряженное состояние возникает в каждой точке круглого вала при кручении?

- Напишите формулу для расчета напряжения в любой точке поперечного сечения?

- Напишите формулу для расчета напряжения на поверхности вала при кручении? Как изменится напряжение, если диаметр вала увеличится в два раза?

- Почему для деталей, работающих на кручение, выбирают круглое поперечное сечение?

- В чем заключается расчет на прочность при кручении?

- В чем заключается расчет на жесткость при кручении?

- Напишите формулу для определения относительного и полного угла закручивания круглого вала.

- Почему при одинаковой прочности и жесткости вал кольцевого поперечного сечения легче, чем вал сплошного круглого сечения?

- Как разрушаются при кручении стержни из пластиче­ского материала? Как объяснить такой тип разрушения?

- Как разрушаются при кручении стержни из хрупкого материала? Как объясняется такой тип разрушения?

- Охарактеризуйте особенности деформации брусьев не кругового сечения. В чем сущность гидродинамической аналогии?

- Как вычислить потенциальную энергию деформации, накапливаемую валом при кручении?

- Почему нельзя для бруса некруглого поперечного сечения вывести методами сопротивления материалов вывести формулу для определения напряжения и угла закручивания?

- Какой из брусьев тонкостенного сечения имеет большее сопротивления кручению: с замкнутым или незамкнутым профилем?

- Какие допущения положены в основу вывода формулы для касательных напряжений, возникающих в поперечном сечении вала при кручении?

- Какое напряженное состояние возникает в каждой точке бруса круглого сечения при кручении?

- В каких точках бруса круглого сечения возникают наибольшее касательное напряжение? Как их вычисляют?

- Что такое полярный момент инерции? Какой физический смысл имеет эта величина? В каких единицах измеряется?

- По каким формулам вычисляют полярные моменты инерции и сопротивления для круглого и кольцевого сечения?

- Что такое полярный момент сопротивления сечения бруса (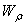)? Получите выражение 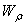для кругового сече­ния?

- Напишите выражение 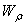для кольцевого сечения? Почему его нельзя вычислять как разность моментов сопротивления наружного и внутреннего кругов?

- Вычислите полярный момент сопротивления сечения круглого сплошного вала d =30 мм?

- Как распределяются касательные напряжения по поперечному сечению вала?

- Как проявляется закон парности касательное напряжение при кручении?

- Как определяется диаметр вала из условия прочности?

- Как определяется диаметр вала из условия жесткости?

- Как изменится напряжение в сечении, если диаметр вала уменьшить в два раза?

- Проведены расчеты вала на прочность и жесткость. Получе­но: диаметр вала из расчета на прочность 65 мм, диаметр вала из расчета на жесткость 70 мм. Каким должен быть вал?

- Как изменится угол закручивания вала, если крутящий момент увеличить в 4 раза, а диаметр уменьшить в 2 раза?

- Как определяется потенциальная энергия при кручении?

- Что называется жесткостью сечения при кручении?

- Что называется полярным моментом сопротивления, в каких единицах он выражается и чему равен (для круга и кольца)?

- Чем объясняется, что вал кольцевого сечения при кручении экономичнее вала сплошного сечения?

- Чему равны наибольшие касательные напряжения и наибольшие главные напряжения в скручиваемом вале круглого сечения? В каких точках они возникают?

- Как разрушаются при кручении стальные чугунные и деревянные валы? Как объяснить характер разрушения для каждого из этих материалов?

- Чему равна потенциальная энергия деформации кручения вала круглого сечения? Запишите соответствующую формулу.

- Как производится расчет вала на прочность при кручении?

- Как выбираются допускаемые напряжения при расчете на кручение?

- Как производится расчет вала на жесткость при кручении?

- Охарактеризуйте расчет статически неопределимых валов.

- Как формулируется закон Гука при сдвиге?

- Какой физический смысл у модуля упругости?

- Чему равен модуль упругости материала при кручении для стали? В каких единицах он измеряется?

- Что представляет собой деформация сдвига?

- Как обозначается деформация при сдвиге?

- Укажите единицы измерения напряжений сдвига и смятия и модуля упругости.

- Какой вид напряженного состояния называют чистым сдвигом?

- Какие виды деформаций испытывает данное соединение?

1) Растяжение и изгиб;

2) Сдвиг и смятие;

3) Изгиб и кручение;

4) Растяжение и сдвиг.

 

- Какая из приведённых ниже формул является математическим выражением закона Гука при сдвиге?

1) ;

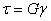2) ;

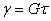3) ;

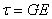4) .

 

- На рисунке изображён вал, на который действуют внешние крутящие моменты: 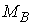=1,5 кНм; 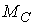=1,5 кНм; 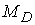=2 кНм; 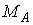=5 кНм. И приведена эпюра внутренних крутящих моментов. На каком участке возникнут наибольшие касательные напряжения?

1) В-С;

2) C-A;

3) A-D.

 

- По какой формуле можно подобрать диаметр вала

1) ;

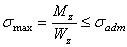2) ;

3) ;

4) .

 

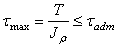- Какая форма сечения вала будет более рациональной (справа приведена эпюра касательных напряжений)?

1) 2)

 

- Условие жёсткости круглого вала при кручении имеет вид:

1) ;

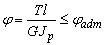2) ;

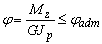3) ;

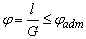4) .

 

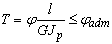- Какие внутренние усилия возникают при сдвиге?

1) Поперечная сила,

2) продольная сила,

3) изгибающий момент.

- Какие внутренние усилия возникают при кручении?

1) Поперечная сила,

2) продольная сила,

3) изгибающий момент,

4) крутящий момент.

 

- Какие виды деформаций испытывает головка болта?

 

 

1) Изгиб с кручением;

2) Сдвиг и смятие;

3) Растяжение.

 

- Закон Гука при сдвиге?

1) ,

2) ,

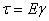3) ,

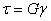4) .

- Условие прочности при кручении.

1) ,

2) ,

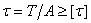3) .

 

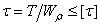- Вал находится в равновесии при

1) ,

2) ,

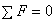3) ,

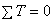4) .

 

- Условие жесткости круглого вала при кручении?

 

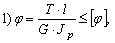
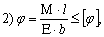
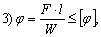
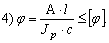
- Как связаны друг с другом при чистом сдвиге значения , , , ?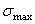

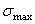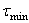1. ; .

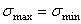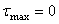2. _.

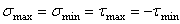3. ; .

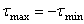4. ; .

 

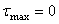- Что называется жесткостью при кручении?

1. ;

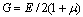2. ;

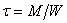3. ;

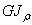4. .

- При каком нагружении прямо брус испытывает деформацию кручения?

1. Кручение происходит при нагружении крутящими моментами.

2. Кручение происходит при нагружении внешними скручивающими моментами, плоскости действия которых перпендикулярны его продольной оси.

3. Кручение происходит при нагружении парами сил.

4. Кручение происходит при нагружении валов и определяется по потребляемой мощности и по частоте вращения вала.

 

- Какое напряженное состояние возникает в каждой точке круглого бруса при кручении?

1. Возникает в точках, наиболее удаленных от центра.

2. Возникает состояние чистого сдвига во всех точках.

3. Во всех точках возникает состояние кручения.

4. Во всех точках возникает состояние сжатия.

 

- Что называется жесткостью сечения при кручении?

1. Жесткостью сечения называется способность сопротивляться нагрузке.

2. Произведение 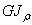называется жесткостью сечения при кручении.

3. Жесткостью сечения при кручении называется разность величин полного и относительного угла закручивания. Единица измерения: нм².

4. Произведение 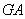называется жесткостью сечения при кручении. Единицы измерения: нм².

 

-Условие прочности вала при кручении:

1. ;

2. ,

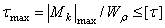3. .

 

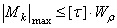- Что характеризует :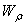

1. площадь сечения

2. напряжение при кручении

3. максимальный угол поворота

 

- Полярный момент сопротивления используется при определении касательных напряжений в сечении вала

1. нет;

2. да;

3. в случае сечения круглой формы.

 

- Полярный момент инерции вала используется для определения его жесткости

1. да;

2. нет;

3. для определения относительного угла закручивания.

 

- Справедлив ли закон Гука при кручении, если напряжение не превышает предела пропорциональности?

1. справедлив;

2. не справедлив.

 

- Зависит ли величина рабочих (расчетных) касательных напряжений от материала вала?

1. зависит;

2. не зависит.

 

- Зависит ли угол поворота сечения вала от материала, из которого он изготовлен?

1. зависит;

2. не зависит.

 

- Во сколько раз уменьшится максимальное напряжение в поперечных сечениях вала, если его диаметр увеличить в два раза?

1. в два раза;

2. в четыре раза;

3. в восемь раз.

 

- Какую механическую характеристику материала листа надо знать, чтобы определить силу, необходимую для продавливания отверстий?

1. предел текучести;

2. предел прочности на растяжение;

3. предел прочности на срез.

 

- Диаметр заклепки увеличился в два раза. Как изменится расчетное напряжение среза?

1. уменьшится в два раза;

2. уменьшится в четыре раза.

 

- Во сколько раз изменится допускаемая нагрузка на сварное соединение, если толщина шва уменьшится вдвое (при прочих равных условиях)?

1. уменьшится в четыре раза;

2. уменьшится вдвое.

Лекция 6. Плоский изгиб

Изгибом называется вид нагружения бруса, при котором к нему прикладывается момент, лежащий в плоскости проходящей через продольную ось. В поперечных сечениях бруса возникают изгибающие моменты. При изгибе возникают деформация, при которой происходит искривление оси прямого бруса или изменение кривизны кривого бруса.

Брус, работающий при изгибе, называется балкой. Конструкция, состоящая из нескольких изгибаемых стержней, соединенных между собой чаще всего под углом 90°, называется рамой.

Изгиб называется плоским или прямым, если плоскость действия нагрузки проходит через главную центральную ось инерции сечения (рис.6.1).

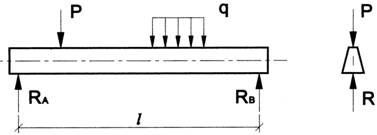
Рис.6.1

 

При плоском поперечном изгибе в балке возникают два вида внутренних усилий: поперечная сила Q и изгибающий момент M. В раме при плоском поперечном изгибе возникают три усилия: продольная N, поперечная Q силы и изгибающий момент M.

Если изгибающий момент 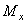является единственным внутренним силовым фактором, то такой изгиб называется чистым (рис.6.2). При наличии поперечной силы 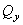изгиб называется поперечным. Строго говоря, к простым видам сопротивления относится лишь чистый изгиб; попереч­ный изгиб относят к простым видам сопротивления условно, так как в большинстве слу­чаев (для достаточно длинных балок) действием поперечной силы при расчетах на проч­ность можно пренебречь.

Косой изгиб - изгиб, при котором нагрузки действуют в одной плоскости, не совпадающей с главными плоскостями инерции.

Сложный изгиб - изгиб, при котором нагрузки действуют в различных (произвольных) плоскостях.

Далее будем рассматривать плоский изгиб, то есть все силы будем прилагать в плоскости симметрии балки.

Рис.6.2

 

Осваивать расчет балок и рам удобно, рассматривая по очереди следующие вопросы:

- Определение внутренних усилий в балках и построение эпюр внутренних усилий.

- Проверка прочности балок.

- Определение перемещений и проверка жесткости балок.

Решение этих вопросов получим в соответствующих разделах на примере конкретных задач.

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: