Построение эпюр поперечной силы и изгибающего момента

Для того, чтобы произвести расчет балки на изгиб, необходимо знать величину наибольшего изгибающего момента М и положение сечения, в котором он возникает. Точно также, надо знать и наибольшую поперечную силу Q. Для этой цели строят эпюры изгибающих моментов и поперечных сил. По эпюрам легко судить о том, где будет максимальное значение момента или поперечной силы.

Перед тем, как определять внутренние усилия (поперечные силы и изгибающие моменты) и строить эпюры, как правило, надо найти опорные реакции, возникающие в закреплении стержня. Если опорные реакции и внутренние усилия можно найти из уравнений статики, то конструкция называется статически определимой. Чаще всего мы встречаемся с тремя видами опорных закреплений стержней: жестким защемлением (заделкой), шарнирно-неподвижной опорой и шарнирно-подвижной опорой. На рис. 6.5 показаны эти закрепления. Для неподвижной (рис 6.5, б) и подвижной (рис. 6.5, в) опор приведены два эквивалентных обозначения этих закреплений. Напомним, что при действии нагрузки в одной плоскости в заделке возникают три опорных реакции (вертикальная, горизонтальная реакции и сосредоточенный реактивный момент) (рис. 6.5, а); в шарнирно-неподвижной опоре – две реактивные силы (рис. 6.3, б); в шарнирно-подвижной опоре – одна реакция – сила, перпендикулярная плоскости опирания (рис.6.5, в).

Рис. 6.5. Опорные реакции: а – в заделке; б – в шарнирно-неподвижной опоре;

в – в шарнирно-подвижной опоре

 

Комбинируя различные типы закреплений, можно получить ряд схем балок:

1. Балка шарнирно опертая по концам (рис.6.6, а). Одна опора шарнирно подвижная, другая – шарнирно неподвижная. Расстояние между центрами опор на схеме называется пролетом. Число реакций равно трем. Учитывая, что для плоской системы сил можно составить три независимых уравнения равновесия системы в целом, приходим к заключению, что балка статически определимая.

2. Балка шарнирно опертая с консолями (С₁ и С₂) (рис.6.6, б). Реакции те же. Балка статически определимая.

3. Балка жестко закрепленная одним концом (консольная балка) (рис.6.6, в). В заделке три реакции. Балка статически определимая. При действии нагрузки перпендикулярной оси реакция Н_В всегда равна 0.

Рис.6.6

 

После определения опорных реакций внутренние усилия в статически определимых конструкциях определяем с помощью метода сечений.

Как было сказано выше, при плоском поперечном изгибе в балке возникают два внутренних усилия: поперечная сила Q и изгибающий момент M. В соответствии с методом сечений поперечную силу можно найти как сумму проекций всех внешних сил, взятых с одной стороны от сечения, на ось, перпендикулярную оси стержня (ось z). Изгибающий момент равен сумме моментов всех внешних сил, взятых с одной стороны от сечения, относительно оси, проходящей через центр тяжести рассматриваемого сечения (оси y).

Для того чтобы можно было вести расчет с любого конца балки, необходимо принять правило знаков для внутренних силовых факторов.

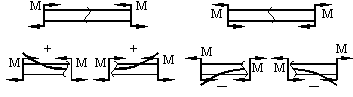
А) б)

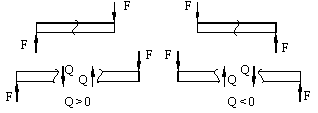
Рис.6.7. а - правило знаков для поперечной силы Q; б - правило знаков для изгибающего момента M.

 

Если внешняя сила вращает отрезанную часть балки по часовой стрелке, то сила является положительной, если внешняя сила вращает отрезанную часть балки против хода часовой стрелки, то сила является отрицательной.

Если под действием внешней силы изогнутая ось балки принимает вид вогнутой чаши, такой, что идущий сверху дождь будет наполнять ее водой, то изгибающий момент является положительным. Если под действием внешней силы изогнутая ось балки принимает вид выпуклой чаши, такой, что идущий сверху дождь не будет наполнять ее водой, то изгибающий момент является отрицательным.

Достаточно очевидно и подтверждается опытом, что балка при изгибе деформируется таким образом, что волокна, расположенные в выпуклой части, растягиваются, а в вогнутой – сжимаются. Между ними лежит слой волокон, который лишь искривляется, не изменяя своей первоначальной длины (рис.6.8). Этот слой называется нейтральным или нулевым, а его след на плоскости поперечного сечения – нейтральной (нулевой) линиейили осью.

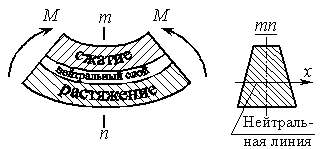
Рис.6.8

 

При построении эпюр Q и М договоримся на эпюре Q положительные значения откладывать сверху нулевой линии. На эпюре М у строителей принято откладывать положительные ординаты снизу. Такое правило построения эпюры М называется построением эпюры со стороны растянутых волокон, т. е. положительные значения М откладываются в сторону выпуклости изогнутой балки.

Рассмотрим для простоты балку с прямоугольным поперечным сечением (рис.6.9). Следуя методу сечений, мысленно проведем разрез и отбросим какую-либо часть балки, а другую оставим. На оставшейся части покажем действующие на нее силы и в поперечном сечении – внутренние силовые факторы, которые являются результатом приведения к центру сечения сил, действующих на отброшенную часть. Учитывая, что внешние силы и распределенные нагрузки лежат в одной плоскости и действуют перпендикулярно оси балки, в сечении получим поперечную силу 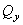и изгибающий момент 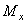. Эти внутренние силовые факторы заранее неизвестны, поэтому их показывают в положительном направлении в соответствии с принятыми правилами знаков.

Рис.6.9

 

На рис.6.9 показаны два случая оставшейся части: левая и правая.

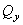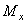Для определения величины и составляются два уравнения равновесия для оставшейся части

Уравнение момента составляется относительно оси Х, проходящей в поперечном сечении через точку на оси балки – тогда поперечная сила в уравнение не входит и величина 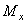определяется независимо от 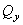. Можно доказать, что результат вычислени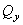й и 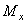не зависит от того, равновесие какой оставшейся части рассматривается.

Рассмотрим характерный пример (рис. 6.10, а) и установим не­обходимые правила. Решение задачи, как правило, начинается с определения полной системы внешних сил. Для этого отбросим опоры и заменим их соответствующими реакциями (рис. 6.10, б), выполняющими ту же роль, что и опорные закрепления.

Заданная система статически определима, следовательно, из ус­ловий равновесия системы, т.е. равенства нулю суммы моментов всех сил относительно шарнирных опор (в шарнирах нет ограниче­ний поворота сечений балки, поэтому изгибающих моментов не возникает) и , определяем вертикальные реакции в опорах:

.

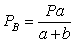Для определения имеем: откуда . Для проверки правильности вычислений воспользуемся усло­вием равенства нулю суммы всех вертикальных сил откуда получим

, 0 = 0.

Рис. 6.10

 

Для определения внутренних силовых факторов - изгибающего момента М (z) и поперечной силы Q (z) как функций от продоль­ной координаты 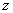, воспользуемся методом сечений. Для полу­чения этих зависимостей балку разбивают на участки, границами которых являются следующие точки: начало и конец балки; точки приложения сосредоточенных усилий; начало и конец действия распределенных усилий; сечения, в которых скачкообразно изменя­ется жесткость балки; в точках, где происходит изменение ориен­тации элементов, если имеем дело с стержневой системой со сложной структурой.

Заданная система состоит из двух участков - первого 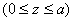и второго . Следовательно, задавая последовательно сечения, принадлежащие к первому и второму участкам, и рассмат­ривая равновесие отсеченных частей системы при действии на них всех внешних сил и внутренних уси­лий, определим выражения для внутренних сило­вых факторов.

Из условия равновесия ; 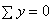отсеченной части системы, расположенной левее от сечения (первый участок), (см. рис. 6.10, в), получим:

; .

Для определения 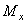и 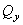на втором участке рассмотрим рав­новесие отсеченной части балки, расположенной правее от сечения z₂ (см. рис. 6.10, б), т.е. ; 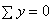откуда и определим:

; .

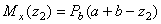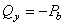Эпюры 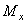и 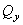изображены на рис. 6.11. Заметим, что эпюры изгибающих моментов 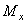, как и поперечных сил 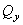строятся на оси бруса, однако в отличие от эпюры поперечных сил знак момента не указывается, а ординаты изгибающего момента откла­дываются co стороны растянутых волокон.

Рис. 6.11

 

⇐ Предыдущая10111213141516171819Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: