 |
Построение эпюр крутящих моментов
|
|
|
|
Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала. Крутящий момент М к в сечении вала числено равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения, при этом могут рассматриваться как левая, так и правая отсеченные части вала.
Примем правило знаков для крутящего момента: его положительное направление соответствует повороту сечения по ходу часовой стрелки, если смотреть на сечение со стороны внешней нормали (рис. 5.2).
Рис.5.2
При наличии распределенной моментной нагрузки m (рис.5.3) крутящие моменты МК связаны дифференциальной зависимостью
(5.1)
из которой вытекает следующая формула:
(5.2)
где 
– крутящий момент в начале участка.
Согласно формуле (5.2) на участках с равномерно распределенной нагрузкой m крутящий момент изменяется по линейному закону. При отсутствии погонной нагрузки (m = 0) крутящий момент сохраняет постоянное значение (МК = МКо = const). В сечениях, где к валу приложены сосредоточенные скручивающие моменты, на эпюре МК возникают скачки, направленные вверх, если моменты направлены против часовой стрелки, либо вниз – при обратном направлении моментов.
Рис. 5.3
Пример 1.
Построить эпюру крутящих моментов для жестко защемленного стержня (рис.5.4, а).
Рис.5.4
Решение.
Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил.
1. Намечаем характерные сечения.
2. Определяем крутящий момент в каждом характерном сечении.
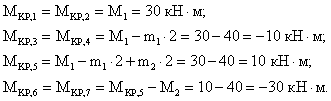
3. По найденным значениям строим эпюру 
(рис.5.4, б).
|
|
|
Напряжения в поперечном сечении
Опыты показывают, что если на поверхности бруса круглого сечения нанести прямоугольную сетку, а на торцевой поверхности нанести радиальные линии (рис.5.5), то после деформации кручение окажется что:
- все образующие поворачиваются на один и тот же угол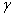 
, а прямоугольники, нанесенные на поверхности, превращаются в параллелограммы;
- торцевые сечения остаются круглыми, плоскими, расстояния между ними не меняются;
- каждое сечение поворачивается относительно другого на некоторый угол 
, называемый углом закручивания;
- радиальные линии на торцевой поверхности остаются прямыми.
На основании этих наблюдений можно заключить, что может быть принята гипотеза Бернулли (гипотеза плоских сечений), а в вале возникают условия чистого сдвига, в поперечных сечениях действуют только касательные напряжения, нормальные напряжения равны нулю.
Рассмотрим поперечное сечение вала, расположенное на некотором расстоянии z от торцевого, где Мк=T (рис.5.5). На элементарной площадке dF будет действовать элементарная сила 
, момент который относительно оси вала равен 
. Крутящий момент М к, в сечении равен
. (5.3)
Рис.5.5
Для того чтобы проинтегрировать это выражение необходимо знать закон распределения напряжений в сечении. Выделим из вала элементарное кольцо длиной dz и толщиной 
(рис.5.6).
Правый торец элемента повернется относительно левого на угол 
, образующая СВ повернется на угол 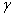и займет положение СВ 1. Угол 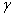- относительный сдвиг. Из треугольника ОВВ 1 найдем:
Рис.5.6 Рис.5.7
.
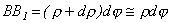Из треугольника СВВ 1: 
. Откуда, приравнивая правые части, получим
.
На основании закона Гука при сдвиге:
. (5.4)
Подставим выражение (5.2) в (5.1):
.
Откуда
. (5.5)
Подставим значение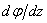 
в выражение (5.4) получим:
.
Таким образом, касательные напряжения при кручении прямо пропорциональны расстоянию от центра тяжести сечения до рассматриваемой точки и одинаковы в точках, одинаково удаленных от центра тяжести сечения (рис. 5.7). При 
получим 
. Наибольшие напряжения возникают в точках контура сечения при 
:
|
|
|
.
Величина отношения полярного момента инерции к радиусу вала называется моментом сопротивления сечения при кручении или полярным моментом сопротивления
.
Для сплошного круглого сечения
.
Для кольцевого сечения
,
где 
.
Тогда максимальные касательные напряжения равны
.
|
|
|
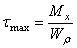