 |
Основные виды напряжённо-деформированного состояния (НДС)
|
|
|
|
До сих пор мы рассматривли в основном простейшие виды НДС – растяжение – сжатие, плоский чистый сдвиг и их комбинацию (рис. 3.3).
А) б) в)
Рис. 3.3
Они встречаются при растяжении и сжатии стержня и его кручении, а также при изгибе (рис. 3.4). При растяжении и сжатии (рис. 3.4, а) осевая 
и поперечные деформации 
, 
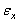определяются законами Гука и Пуассона:
(11)
А) Растяжение б) Кручение
В) Изгиб
Рис. 3.4
При плоском чистом сдвиге (рис. 3.4, б) деформация сдвига
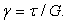(12)
Часто на практике встречаются двухосное растяжение и его комбинация с чистым сдвигом (рис. 3.5).
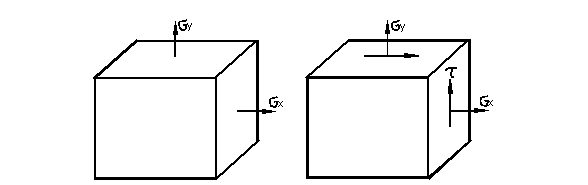
А) б)
Рис. 3.5
В последнем случае состояние называют плоским напряжённым состоянием. Оно возникает в тонкостенных элементах конструкций, таких как плиты (пластины) и оболочки (рис. 3.6).
При двухосном растяжении деформации в направлениях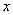 
и 
могут быть найдены на основании законов (11) для одноосного растяжения. Представим 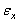, на основании принципа независимости действия сил (напряжений 
, 
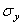) в виде суммы деформаций в каждом из направлени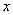й и от этих сил:
(13)
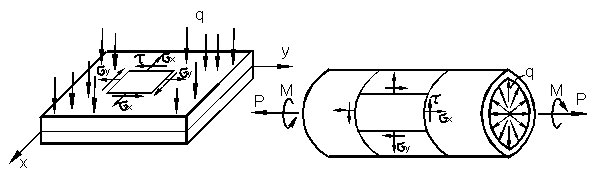
А) б)
Рис. 3.6
Для плоского напряжённого состояния (рис. 3.6, б) с учётом (12) получаем:
(14)
При трёхосном растяжении (рис. 3.7, а) на основании законов (11) аналогичным образом получаем:
(15)
А) Трёхосное б) Плоская в) Объёмное напряжённое
Растяжение деформация состояние
Рис. 3.7
Если сложить соотношения (15), то получим закон упругого изменения объёма:
(16)
где 
– относительное изменение объёма, (17)
– модуль объёмной деформации. (18)
На практике часто встречается напряжённое состояние, изображённое на рис. 3.7, б. Оно возникает в удлинённых телах со стеснённой в этих направлениях деформацией. Примером могут служить подпорная стенка, тело плотины, железнодорожный рельс и др. В этих случаях призматическое тело как бы зажато между двумя опорами, а нагрузка вдоль тела остаётся неизменной (рис. 3.8).
|
|
|
А) б) в) г)
Рис. 3.8
Произвольная точка А тела при деформации остаётся лежать в одной плоскости, параллельной плоскости 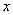, . Напряжённое состояние отличается от плоского тем, что возникает напряжение 
. Соответствующее деформированное состояние тела носит название плоской деформации. Относительные деформации определяются соотношениями закона Гука, полученные использованием принципа независимости действия сил (напряжений). Накладывая на соотношения (5) при трёхосном растяжении плоский чистый сдвиг с напряжениями 
получаем:
(19)
Характерным примером возникновения объёмной НДС могут служить контактные задачи. Например, задачи о контакте колёс вагона с рельсами, задача о вдавливании шарика в подшипнике, шаровой опоры в фундамент и др. (рис. 3.9, а).
Общий случай НДС. Обобщённый закон Гука-Коши
Рассмотрим далее общий случай объёмного напряжённо-деформированного состояния (рис. 3.10).
Рис. 3.10
Его можно разложить на сумму двух состояний – трёхосное растяжение и сложный сдвиг в трёх координатных плоскостях. На основании принципа независимости действия сил (напряжений), используя (19) и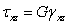 
, 
, получаем:
Вопросы для самопроверки
- Что понимается под напряженным состоянием в точке твердого тела, если оно нагружено внешними силами?
- Объясните понятие тензор напряжений?
- Какие напряжения называются главными?
- Чем характеризуется и как изображается напряженное состояние в точке?
- Какие площадки и какие напряжения называют главными?
- Чем характеризуется деформированное состояние в точке?
- Сколькими параметрами определяется плоское напряженное состояние точки? Назовите эти параметры?
|
|
|
- В каких случаях возникают предельные напряженные состояния у пластичных и хрупких материалов?
- Сформулируйте закон парности касательных напряжений?
- Какие существуют типы напряженного состояния в точке тела, чем они отличаются?
- Что понимается под линейным напряженным состоянием?
- Что понимается под плоским напряженным состоянием?
- Что понимается под объемным напряженным состоянием?
- Какое напряженное состояние называется пространственным (трехосным), плоским (двухосным) и линейным (одноосным)?
- Понятие о сложном напряженном состоянии.
- Дайте определение главных площадок и главных напряжений. Получите выражения для определения положения главных площадок и величин главных напряжений?
- Какие площадки называются главными?
- Соотношение между главными напряжениями.
- Каково правило законов для нормальных и касательных напряжений?
- Чему равна сумма нормальных напряжений, действующих на любых двух взаимно перпендикулярных площадках?
- Что такое главные напряжения и главные площадки? Как расположены главные площадки относительно друг друга?
- Чему равны касательные напряжения на главных площадках?
- Как вычислить максимальные касательные напряжения в точке тела при одноосном напряженном состоянии? По каким площадкам они действуют?
- Как вычислить максимальные нормальные и касательные напряжения при плоском и объемном напряженных состояниях?
- Как связаны главные напряжения и максимальные касательные напряжения при чистом сдвиге?
- Как определить значение главных напряжений при плоском напряженном состоянии?
- Напишите формулы для определения главных напряжений и углов наклона главных площадок.
- Как определить положение главной площадки, по которой действует главное напряжение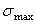 
в общем случае плоского напряженного состояния?
- Чему равны максимальные значения касательных напряжений в случае плоского напряженного состояния?
- Какие площадки называются площадками сдвига и под каким углом они наклонены к главным площадкам?
- Чему равна сумма нормальных напряжений на любых трех взаимно перпендикулярных площадках?
- Чему равны максимальные и минимальные касательные напряжения (при заданных напряжениях 
, 
, 
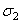) и по каким площадкам они действуют?
|
|
|
- Докажите свойство парности (взаимности) касательных напряжений и получите выражения для нормального и касательного напряжения в наклонной площадке?
- Какими выражениями определяются величины экстремальных касательных напряжений и как расположены площадки, в которых они действуют?
Лекция 5. Кручение, сдвиг, срез
Кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис. 5.1).
Стержни круглого или кольцевого сечения, работающие на кручение, называют валами. При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.
Пусть вал вращается с постоянной скоростью n об/мин. и передает мощность N Нм/с. Угловая скорость вращения вала равна 
(рад/сек), а передаваемая мощность 
.
Скручивающий момент равен 
.
Если мощность задана в киловаттах, то величина скручивающего момента определяется по формуле
.
|
|
|
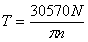