 |
3. Закон Ньютона для вязкости, параметры характеризующие вязкость, физический смысл этих параметров, единицы измерения параметров вязкости.
|
|
|
|
3. Закон Ньютона для вязкости, параметры характеризующие вязкость, физический смысл этих параметров, единицы измерения параметров вязкости.
Вязкость – свойство жидкости оказывать сопротивление относительному сдвигу слоев. Вязкость проявляется в том, что при относительном перемещении слоев жидкости на поверхностях их соприкосновения возникают силы сопротивления сдвигу Т, называемые силами внутреннего трения, или силами вязкости
Вязкость проявляется для большинства жидкостей только при движении. Но у некоторых жидкостей, например нефтепродуктов, смазочных масел при низких температурах, коллоидных растворов и в состоянии покоя имеются силы трения. Такие жидкости называются аномальными (неньютоновскими).
Законы продольного внутреннего трения были установлены Ньютоном в 1686 г. Эти законы можно сформулировать так:
Сила Т продольного внутреннего трения в параллельноструйном потоке жидкости, то есть сила трения, возникающая при скольжении отдельных прямолинейных слоев жидкости друг по другу:
1) прямо пропорциональна так называемому градиенту скорости;
2) прямо пропорциональна площади S поверхности соприкасания данных слоев жидкости;
3) не зависит от давления;
4) зависит от физических свойств жидкости (от рода жидкости), а следовательно, и от ее температуры
Законы Ньютона можно представить в аналитической форме:
,
где m – некоторый коэффициент пропорциональности, называемый, как отмечалось выше, динамическим коэффициентом вязкости или просто коэффициентом вязкости. Величина m зависит от рода жидкости, а также от ее температуры; чтобы подчеркнуть это обстоятельство, иногда m называют коэффициентом молекулярнойилифизической вязкости. Численные значения m для различных жидкостей находятся опытным путем при помощи особых приборов, называемых вискозиметрами.
|
|
|
4 ОСНОВНОЕ УРАВНЕНИЕ ГИДРОСТАТИКИ
Рассмотрим жидкость, покоящуюся в сосуде, неподвижном относительно Земли (рис. 3. 4).
Для рассматриваемого случая действующей на жидкость массовой силой является только сила тяжести.
Направив ось OZ вертикально вверх, получим Fx = 0, Fy = 0,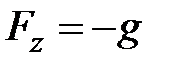 
, а подставив полученные величины в уравнение (3. 1), получим:
,
что можно переписать в виде:
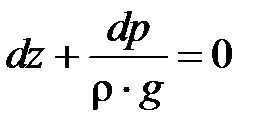. (3. 5)
Интегрируя дифференциальное уравнение (3. 5), получаем:
, (3. 6)
где С – постоянная интегрирования.
Значение постоянной интегрирования С определяется из известных граничных условий: р = р0 при z = z0. Подставляя эти условия в уравнение (3. 6), имеем:
. (3. 7)
Подставляя выражение (3. 7) в (3. 6) получаем:
, (3. 8)
или с учетом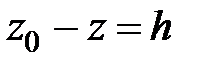 
:
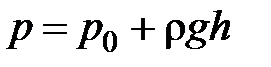. (3. 9)
Уравнение (3. 8) называется основным уравнением гидростатики. Уравнение (3. 9) представляет вторую форму основного уравнения гидростатики.
Основное уравнение гидростатики является математическим выражением закона распределения гидростатического давления в жидкости: гидростатическое давление в некоторой точке, погруженной на глубину h относительно свободной поверхности, равно сумме внешнего давления р0, действующего на свободную поверхность жидкости, и давления столба жидкости высотой, равной глубине погружения рассматриваемой точки h, с площадью основания, равной единице.
Основным законом (уравнением) гидростатики называется уравнение[1]:
,
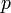— гидростатическое давление (абсолютное или избыточное) в произвольной точке жидкости,
— плотность жидкости,
|
|
|
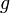— ускорение свободного падения,
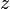— высота точки над плоскостью сравнения (геометрический напор[2]),
— гидростатический напор[3].
Уравнение показывает, что гидростатический напор во всех точках покоящейся жидкости является постоянной величиной.
Иногда основным законом гидростатики называют принцип Паскаля[4].
|
|
|
