 |
11.Расход. Уравнение расхода. Расходом называется количество жидкости, протекающее через живое сечение потока в единицу времени. Это количество можно измерить в единицах объема, в весовых единицах, в единицах массы в связи, с чем различают объемный Q, вес
|
|
|
|
11. Расход. Уравнение расхода
Расходом называется количество жидкости, протекающее через живое сечение потока в единицу времени. Это количество можно измерить в единицах объема, в весовых единицах, в единицах массы в связи, с чем различают объемный Q, весовой QG и массовый расходы Qm.
Для элементарной струйки, имеющей бесконечно малые площади сечений, можно считать истинную скорость одинаковой во всех точках каждого сечения. Следовательно, для этой струйки расходы равны.
объемный, (м3/с) dQ = v*dS, (5. 136)
весовой, (Н/с) dQG = ρ g*dQ, (5. 2)
массовый, (кг/с) dQm = ρ v*dS, (5. 3)
где dS – площадь сечения струйки.
Для потока конечных размеров в общем случае скорость имеет различное значение в разных точках сечения, поэтому расход надо определять, как сумму элементарных расходов струек в данном сечении.
Q =. (5. 4)
Обычно в рассмотрение вводят среднюю по сечению скорость vср = Q/S, откуда средний расход для струйки или потока равен Qср = vср*S. (5. 5)
Условие неразрывности потока основывается на следующих свойствах, законе и предпосылках. а) трубка тока имеет свойство непроницаемости для внешних, обтекающих ее потоков; б) закон сохранения вещества; в) предположение о сплошности (неразрывности) среды для установившегося течения несжимаемой жидкости. На основании этих предпосылок и свойств можно утверждать, что объемный расход во всех сечениях элементарной струйки (см. рис. 5. 2) один и тот же
dQ = v1 *dS1 = v2 *dS2 → const (вдоль струйки). (5. 6) Это уравнение называется уравнением объемного расхода для элементарной струйки.
Аналогичное уравнение можно составить и для потока конечных размеров, ограниченного непроницаемыми стенками, только вместо истинных скоростей следует ввести средние скорости. В результате Q = vср1 *S1 = vср2 *S2 → const (вдоль потока). (5. 6’)
|
|
|
Из последнего уравнения следует, что средние скорости в потоке несжимаемой жидкости обратно пропорциональны площадям сечений:
vср1 / vср2 = S1/S2
Уравнение расхода (5. 6‘) является следствием общего закона сохранения вещества для частных условий, в частности? для условий сплошности (неразрывности) течения.
12. Уравнение Бернулли для элементарной струйки
идеальной жидкости
Рассмотрим установившееся течение идеальной жидкости находящейся под действием одной массовой силы — силы тяжести, и выведем для этого случая основное уравнение, связывающее между собой давление в жидкости и скорость ее движения.
Возьмем одну из элементарных струек, составляющих поток, выделим сечениями 1 и 2 участок этой струйки произвольной длины (рис. 5. 3). Пусть площадь первого сечения равна dS1 , скорость в нем V1 , давление P1, а высота от произвольной плоскости сравнения Z1. Во втором сечении dS2, V2, P2 и Z2.
За бесконечно малый отрезок времени dt выделенный участок струйки переместится в положение 1’ – 2’.
Применим к массе жидкости в объеме участка струйки теорему о кинетической энергии: работа сил, приложенных к телу, равна приращению кинетической энергии этого тела.
На жидкость действуют силы тяжести и силы давления, нормально к поверхности сечения рассматриваемого участка струйки.
Подсчитаем работу сил давления, сил тяжести и изменение кинетической энергии участка струйки за время dt. Эта теорема выглядит следующим образом. (m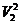 
)/2 - (m 
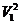)/2 = G*h= G*(Z1-Z2) Работа силы давления в первом сечении положительна, так как направление силы совпадает с направлением перемещения, и выражается как произведение силы p1*dS на путь V1dt: p1*dS1)*(V1dt) Работа силы давления во втором сечении имеет знак минус, так как направление силы прямо противоположно направлению перемещения, и определяется выражением - (p2*dS2) *(V2dt). Силы давления, действующие по боковой поверхности отрезка струйки, работы не производят, так как они нормальны к этой поверхности и к перемещениям.
|
|
|
Работа сил давления равна dA = (p1*dS1) *( V1dt)— (p2*dS2) *(V2dt). Работа силы тяжести равна изменению потенциальной энергии положения участка струйки, поэтому надо из потенциальной энергии жидкости в объеме 1 - 2 вычесть потенциальную энергию жидкости в объеме 1’- 2’. При этом энергия промежуточного объема 1’- 2 сократится, и останется лишь разность энергии элементов 1- 1’, 2- 2’. ПО уравнению расходов (закон сплошности среды) (5. 6’) объемы и силы тяжести заштрихованных элементов 1 -1’ и 2 - 2’ равны между собой: dG = ρ *g* V1*dS1*dt = ρ *g* V2*dS2*dt Тогда работа силы тяжести выразится как произведение разности высот на силу тяжести dG: (z1-z2) *dG Чтобы подсчитать приращение кинетической энергии рассматриваемого участка струйки за время dt, необходимо из кинетической энергии объема 1’- 2’ вычесть кинетическую энергию объема 1 - 2. При вычитании кинетическая энергия промежуточного объема 1’ - 2 сократится, и останется лишь разность кинетических энергий элементов 2 — 2’ и 1 - 1’, масса каждого из которых равна dG/g. Таким образом, приращение кинетической энергии на участке струйки равно (v22- v21)* dG/(2g), Сложив работу сил давления (см. уравнение 5. 7) с работой силы тяжести (5. 9) и приравняв эту сумму приращению кинетической энергии (5. 10), получим исходное уравнение для трех видов уравнения Бернулли. (p1*dS1) *( v1dt)— (p2*dS2) *( v2dt) +(z1-z2) *dG=(v22- v21)* dG/(2g) Разделим это уравнение на dG ( изменение силы тяжести элементарной струйки за время dt) (см. формулу (5. 8), и произведя сокращения на dG = ρ *g* v1*dS1*dt = ρ *g* v2*dS2*dt , получим 
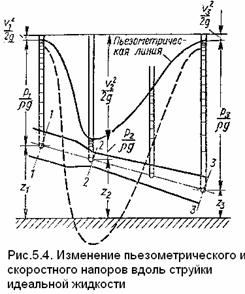
Сгруппируем члены, относящиеся к первому сечению, в левой части уравнения, а члены, относящиеся ко второму сечению, в правой: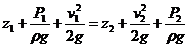 
где z — геометрическая высота, или геометрический напор; Р/ρ g – пьезометрическая высота или пьезометрический напор; v2/2g — скоростная высота или скоростной напор. Полученное уравнение называется уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости. Оно было выведено Даниилом Бернулли в 1738 г. Это уравнение является первой формой уравнения Бернулли, оно 
(5. 13) называется полным напором и имеет размерность длины.
|
|
|
Данное уравнение получено путем деления исходного уравнения (5. 11), выражающего теорему об изменении кинетической энергии элементарной струйки, на ее изменении ее силы тяжести за время dt. Уравнение Бернулли (5. 13) записано для двух произвольно взятых сечении струйки и выражает равенство полных напоров Н в этих сечениях. Так как сечения взяты произвольно, следовательно, и для любого другого сечения этой же струйки полный напор будет иметь то же значение
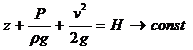(вдоль струйки)
Для идеальной движущейся жидкости вдоль струйки тока сумма трех напоров: геометрического, пьезометрического и скоростного есть величина постоянная. На рис. 5. 4 показано изменение всех напоров вдоль струйки. Линия изменения уровней жидкости в пьезометрах называется пьезометрической линией. Из уравнения Бернулли и уравнения расхода следует, что если площадь поперечного сечения струйки уменьшается, т. е. струйка сужается, то скорость течения жидкости увеличивается, а давление уменьшается, и наоборот, если струйка расширяется, то скорость уменьшается, а давление возрастает. На рис. 5. 4 площадь поперечного сечения струйки от сечения 1 - 1 к сечению 2 - 2 уменьшается в 4 раза, скоростной напор увеличивается в 16 раз, а сечение 3 - 3 имеет ту же площадь, что и сечение 1-1. Штриховой линией показано положение пьезометрической линия при тех же сечениях и при увеличении расхода в 
раз, вследствие чего скоростные высоты увеличиваются в 2 раза, а в узкой части струйки давление становятся меньше атмосферного. Уравнение Бернулли можно записать в двух других формах. Разделив уравнение (5. 11) на расход dQ = dS1*v1dt = dS2*v2dt, учитывая, что dG = ρ *g*dQ, а dQ = dG/ρ g, получим
p1 - p2 +(z1-z2) * ρ *g = ρ * (v22- v21)/2. или
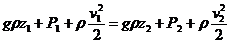, (5. 15)
где все величины выражены в виде давлений.
В этой форме члены уравнения Бернулли имеют размерность давления и имеют следующие называния: ρ zg — весовое давление; р — гидромеханическое давление; ρ v2/2 — динамическое давление. Разделив уравнение (5. 11) на массу dmэлементарного объема, равную (ρ * v1*dS1) *dt = (ρ * v2*dS2) * dt и преобразуем это уравнение подобно предыдущему. Тогда вместо выражения (5. 15) будем иметь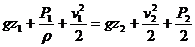 
(5. 16)Введем понятие удельной энергии жидкости, в качестве которой рассмотрим отношение энергии к массе или объему. Нетрудно показать, что члены уравнения (5. 16) представляют собой различные формами удельной механической энергии, а именно: gz — удельная потенциальная энергия (ее еще называют энергией положения), так как частица жидкости массой Δ m, находясь на высоте z, обладает энергией равной Δ mgz, а на единицу массы приходится энергия gΔ mz/Δ m =gz; р/ρ - удельная энергия давления (движущейся) жидкости, так как частица массой Δ m при давлении р обладает способностью подняться на высоту h = р/ρ g и приобрести, таким образом, энергию положения Δ mgр/(ρ g) = р/ρ (после деления на Δ m получаем р/ρ ); сумма gz + р/ρ – удельная потенциальная энергия жидкости; v2/2 - удельная кинетическая энергия жидкости, так как для той же частицы Δ m кинетическая энергия отнесенная к ее массе Δ m v2/2 : Δ m = v2/2; Hg = zg+p/ρ + v2/2 – полная удельная механическая энергия движущейся жидкости.
|
|
|
Таким образом, энергетический смысл уравнения Бернулли для элементарной струйки идеальной жидкости заключается в постоянстве вдоль струйки полной удельной энергии жидкости. Механическая энергия жидкости может иметь три формы: потенциальная энергия, энергия давленияи и кинетическая энергия. Первая и третья формы механической энергии известны из механики, они свойственны твердым и жидким телам. Энергия давления является специфической для движущихся жидкостей. В процессе движения идеальной жидкости одна форма энергии может превращаться в другую, однако полная удельная энергия идеальной жидкости при этом как следует из уравнения Бернулли, остается без изменений. Энергию давления легко преобразовать в механическую работу. Простейшим устройством, с помощью которого осуществляют такое преобразование, является цилиндр с поршнем (рис. 5. 5). Покажем, что при этом преобразовании каждая единица массы жидкости совершает работу, численно равную р/ρ. Пусть площадь поршня равна s, его ход L, избыточное давление жидкости в левой полости цилиндра необходимое для преодоления силы F равно Р = F/S, избыточное давление по другую сторону поршня равно нулю. Преодолевая силу F при перемещении поршня из левого положения, давление совершает работу А = РSL. Расход жидкости, которую необходимо подвести к цилиндру для совершения этой работы за время t, равен объему цилиндра, т. е. Q t = W =SL. Удельная работа, приходящаяся на 1 кг массы, е = А/m = pSL /( SLρ ) = р/ρ .
|
|
|
|
|
|
