7. Давление жидкости на цилиндрические стенки

Рассмотрим (рис. 3. 20) некоторую ограниченную часть твердой цилиндрической поверхности, которую назовем цилиндрической стенкой. Пусть рассматриваемая стенка находится под односторонним воздействием покоящейся жидкости, которое сводится к тому, что в каждой точке на стенку действует давление жидкости. Разобьем стенку на элементарные площадки. В силу малости площадок будем считать их плоскими и выразим элементарную силу давления на них в общем виде dP = pdw. Силы dP уже не будут направлены параллельно друг другу, их линии действия могут не пересекаться в одной точке, и их сумма может не сводиться к одной равнодействующей.

Для шаровой или круговой цилиндрической стенки элементарные силы давления, будучи нормальными к элементарным площадкам на этих поверхностях, направлены по радиусам и, следовательно, пересекутся в центре сферы или в центре круга (поперечного сечения цилиндра).

Определение сил давления на цилиндрические и шаровые поверхности имеет большое значение, так как в гидротехнических сооружениях обычно применяются конструкции с такими поверхностями (секторные, сегментные, вальцовые и шаровые затворы, водонапорные баки и т. п. ).

Рассмотрим цилиндрические стенки, находящиеся под односторонним воздействием покоящейся жидкости. Определим силу избыточного давления. При этом условимся одну из осей координат направлять вдоль образующей цилиндрической поверхности.

Цилиндрическая поверхность с горизонтальной образующей. Направим ось OY параллельно образующей (рис. 3. 20), а ось OZ – вертикально вверх.

Значение силы давления на цилиндрическую поверхность в данном случае определяется следующим образом:

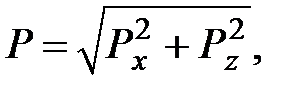                                     (3. 17)

где Р_х и Р_z  –горизонтальная и вертикальная составляющие силы давления.

Выделим на цилиндрической поверхности элементарную площад­ку dw, на которую действует направленная по нормали элементарная сила dP = rghdω . Найдем горизонтальную dP_x и вертикальную dP_у составляющие силы dP:

.

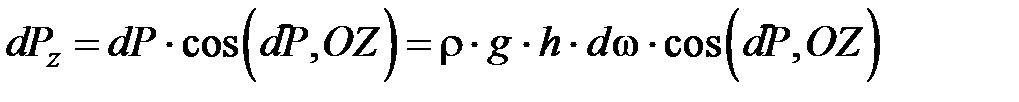Интеграл 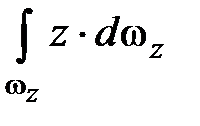 представляет собой объем призмы, ограниченной снизу цилиндрической поверхностью, а сверху – ее проекцией w_z на пьезометрическую плоскость. Направляющие этой призмы – вертикальные прямые. Полученное таким образом тело называется телом давления. Тело давления – это объемная фигура, ограниченная снизу цилиндрической поверхностью, по бокам вертикальными плоскостями, проходящими через крайние точки цилиндрической поверхности, и сверху горизонтальной плоскостью, совпадающей с пьезометрической.

Горизонтальная составляющая Р_х проходит через центр давления проекции w_х, а вертикальная составляющая Р_z проходит через центр тяжести тела давления.

Направление вертикальной составляющей Р_z для схемы, изображенной на рис. 3. 20, а – вниз, а на рис. 3. 20, б –  вверх.

Направление линии действия силы Р определяется направляющими косинусами:

8. Плавание тел.

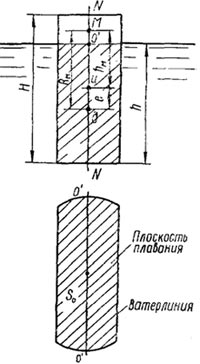
На всякое тело, полностью или частично погруженное в жидкость, действуют две силы: сила тяжести G = γ _т·V и архимедова сила Р, равная весу жидкости в объеме погруженной части тела, G = γ ·V В вышеприведенных выражениях γ _т и γ — соответственно удельные веса тела и жидкости; V— объемное водоизмещение, т. е. объем жидкости, вытесненной телом. Сила тяжести приложена в центре тяжести тела — точке ц. Архимедова сила направлена вверх и приложена в центре объемного водоизмещения — точке д(см. рисунок). В однородном теле, полностью погруженном в жидкость, точки ц и дсовпадают. Различают три случая плавания тел: