Соотношение неопределенностей Гейзенберга

Теория Бора оказалась недостаточной для объяснения многих явле­ний микромира — строения многоэлектронных атомов, молекул, химиче­ской связи и т. д. Идеи де Бройля и выявленные на опыте волновые свой­ства частиц вещества послужили толчком к созданию принципиально новой теории, описывающей поведение микрочастиц с учетом их волно­вых свойств. Этой теорией стала квантовая (волновая) механика, основы которой были созданы в 1925—1926 гг. В. Гейзенбергом и Э. Шредингером.

После беседы с Н. Бором 20 летний студент Мюнхенского университета Вернер Гейзенберг пришел к выводу, что в последова­тельной и логически непротиворечивой теории атома нельзя использовать законы ньютоновской механики и потому следует отказаться от такого клас­сического понятия, как «электронная орбита».

В течение трех лет Вернер Гейзенберг думал над тем, какой должна быть новая механика микрочастиц. Статья Гейзенберга «О квантово-механическом истолковании кинема­тических и механических зависимостей» (от 27.07.1925 г.) явилась первым шагом к созданию совершенно новой теории микромира — квантовой ме­ханики.

Квантовая механика представляет собой нерелятивистскую теорию явлений, происходящих в микромире. Ее отличительной чертой является учет корпускулярно-волнового дуализма и вероятностное описание поведения микрочастиц.

Квантовая механика раскрывает два основных свойства вещества: квантованность внутриатомных процессов и волновую природу частиц.

Квантовая механика лишена наглядности, характерной для класси­ческой механики. Образы привычного нам макромира становятся непри­годными для описания явлений, происходящих в микромире.

Для того чтобы описать поведение любой частицы, нужно опреде­лить ее координату х, импульс р, энергию Е и т. д.

В классической механике считалось, что если выбрана та или иная система отсчёта, то любая движущаяся частица в каждый момент времени будет иметь в ней определённые координаты и скорость. Зная начальные значения этих величин, можно было определить их значения в последующие моменты времени и тем самым предсказать, где будет находится частица в той или иной момент времени. Однако опыты с микрочастицами (например, дифракционные эксперименты Дэвиссона и Джермера) показали, что в микромире такие предсказания невозможны. Здесь можно говорить лишь о вероятности обнаружения данной частицы в той или иной точке пространства. Предсказать же, в какую именно точку экрана в опыте Дэвиссона и Джермера попадёт конкретный электрон, принципиально невозможно.

Неспособность классической механики объяснить результаты подобных экспериментов обусловлены тем, что в ней не учитываются волновые свойства микрочастиц. Учёт и корпускулярных и волновых свойств частиц был осуществлён в квантовой механике.

Согласно квантовой механике для микрочастиц не существует понятие траектории, и потому проследить во всех деталях за их движением невозможно.

Так как движущаяся частица обладает корпускулярно-волновым дуализмом, то одновременное точное определение координаты х и импульса р_х невозможно.

Тщательный анализ поведения микроскопических частиц, проведен­ный Гейзенбергом, показал, что существует принципиальный предел точности измерений указанных величин. Если обозначить Δх, Δу, Δz не­точность (неопределенность) определения координаты, а Δр_х, Δр_у, Δр_z — неточность (неопределенность) определений соответствующих проекций импульса, то эти величины между собой связаны зависимостями

ΔхΔр_х ≥ ħ, ΔyΔр_y ≥ ħ, ΔzΔр_z ≥ ħ (26.3)

Эту зависимость называют соотношением неопределенностей Гейзенберга.

Из него следует: чем точнее определена координата (Δх→ 0), тем менее точно определен импульс (Δр_х→ ∞), и наоборот. Т аким образом, соотношение неопределенностей устанавливает пре­делы, за которыми принципы классической физики становятся неприем­лемыми. Если произведение Δ х Δ р сравнимо с ħ, то поведение частицы описывается законами квантовой механики, если Δ х Δ р велико по сравне­нию с ħ, то поведение частицы описывается законами классической физики.

Из соотношения неопределённостей следует также, что в микромире невозможна локализация частицы в сколь угодно малой области пространства. Другими словами, если бы мы захотели, скажем, поймать и удерживать в каком-либо месте электрон, то у нас бы из этого ничего не вышло.

В самом деле, в процессе сжатия области локализации неопределённость Δх в местоположении частицы будет становиться всё меньше и меньше. Но тогда разброс в возможных значениях её скорости

будет становиться всё больше и больше. Из-за этого будет расти и неопределённость её кинетической энергии. Рано или поздно энергия частицы возрастёт настолько, что эту частицу будет невозможно удержать в одном месте и, преодолев удерживающие её силы, она покинет область локализации. Описанное явление называют туннельным эффектом.

Соотношение, аналогичное (7.21), имеет место для времени и энергии:

ΔЕ Δt > h (26.4)

Рассмотрим это соотношение в применении к возбужденному со­стоянию атома. Если считать Δt средним временем жизни возбужденного состояния атома, а ΔЕ — средней шириной его энергетического уровня (неопределенность энергии состояния), то чем короче время существова­ния какого-либо состояния системы, тем более неопределенно значение его энергии.

При переходе атома из возбужденного в нормальное состояние излучается квант энергии, характеризуемый некоторой частотой размытости Δν = ΔЕ/h спектральной линии излучения, что приводит к уширению спектральных линий.

Гейзенберг и Бор показали, что ни одно измерение не может дать результатов, противоречащих соотношениям неопределенностей. Эти соот­ношения являются одним из фундаментальных положений квантовой механики.

При движении электрона в атоме соотношение неопределенностей вносит существенные изменения в представления о траектории электро­на, т. е. его орбите.

Радиус первой боровской орбиты атома водорода г = 0,5·10^-10 м. Скорость электрона на орбите υ ≈ 10⁶м/с.

Если предположить, что скорость определена с точностью всего 10%, т. е.

Δυ≈ 10⁶м/с, то неопределенность координаты

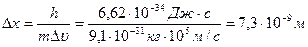
что почти в 150 раз превышает радиус орбиты.

Таким образом, классическое понятие траектории (орбиты) для элек­трона в атоме теряет смысл.

Для макроскопических тел ограничения, накладываемые соотноше­нием неопределенностей Гейзенберга, совершенно несущественны.

Например, для маленькой капли диаметром 0,1 мм (m= 5·10^-10 кг), движущейся со скоростью υ = 10 м/с, измеренной с точностью до 10%, т. е. при Δр = mΔυ= 5· 10^-10кг·м/с, неопределенности координаты Δx=10^-24 м, что в 10²⁰ раз меньше диаметра капли.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: