Понятие о линейном гармоническом осцилляторе

В общем случае на квантование энергии частицы влияет форма по­тенциальной ямы. Пусть частица массой m удерживается в определенной области пространства под действием силы F = -kx, т. е. совершает коле­бания. Потенциальная энергия этой частицы

(26.26)

[ω₀², = k/m— собственная циклическая частота;

k — коэффициент квази­упругой силы].

Уравнение Шредингера для этой частицы, являющейся линейным гармоническим осциллятором, имеет вид

(26.27)

(Е – полная энергия частицы).

Потенциальной ямой для линейного гармонического осциллятора будет область оси ОХ, ограниченная кривой потенциальной энергии (рис.7.6).

Решение уравнения (7.44) позволяет определить полную энергию гармонического осциллятора:

Е_n=hν₀ (n+1/2) (n=0, 1, 2….) (26.28)

ν₀ = ω₀/2π

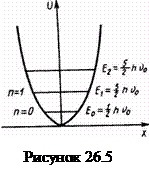
На рис. 7.6 представлены энергетические уровни линейного гармо­нического осциллятора. Из формулы (26.28) вытекает, что осциллятор имеет дискретный спектр значения энергии Е₁, Е₂,..., расположенных на одинаковых энергетических расстояниях друг от друга.

Наименьшая энергия Е₀ = 1/2 hν₀, которую может иметь гармонический осциллятор, называется нулевой энергией. Величина Е₀ никогда не обращается в нуль, в том числе и при Т = О К.

Существование нулевой энергии подтверждается экспериментально при изучении явления рассеяния света кристаллами при температуре, близкой к абсолютному нулю. Рассеяние света происходит на колеблю­щихся атомах, молекулах или ионах, расположенных в узлах кристалли­ческой решетки. Экспериментально установлено, что при уменьшении температуры интенсивность рассеянного света не убывает ниже некото­рого предела. Таким образом, при сверхнизкой температуре, близкой к абсолютному нулю, существует нулевая энергия.

Наиболее простым примером потенциального барьера является од­номерный барьер прямоугольной формы высотой U, шириной ℓ, частица движется вдоль оси X (рис. 7.7, а):

0, х < 0 (для области 1)

U(x)= U, 0<х<ℓ (для области 2),

0, х > ℓ (для области 3).

Если эту задачу решать для классической частицы, обла­дающей энергией Е, то она либо пройдет над барьером (при Е > U), либо отразится от него и будет двигаться в обратную сторону (при Е<U).

Из решения уравнения Шредингера, описывающего дви­жение микрочастицы при данных условиях (26.27), следует:

• если частица обладает энергией Е > U, то имеется от­личная от нуля вероятность того, что частица отразится от барьера и будет двигаться в обратную сторону;

• если энергия частицы Е < U, то имеется отличная от нуля вероят­ность того, что частица проникает сквозь потенциальный барьер и окажется в области х > ℓ.

Уравнение Шредингера для каждой из выделенных на рис. 26.6, б об­ластей имеет вид

(для области 1,3) (26.29)

(для области 2) (26.30)

Из решения этих дифференциальных уравнений следует:

• в области 1 будет как плоская волна, распространяющаяся в положи­тельном направлении оси X, соответствующая частице, движущейся в направлении к барьеру, так и волна, отраженная от барьера, соот­ветствующая частице, движущейся от барьера;

• в области 2 даже при условии Е < U волновая функция не равна нулю;

• в области 3 (если барьер не очень широк) будет волна, прошедшая сквозь барьер, распространяющаяся слева направо, имеющая такую же частоту, как в области 1, но меньшую амплитуду. Качественный вид функций ψ₁(x), ψ ₂(х), ψ₃(х) показан на рис. 7.7, б. Таким образом, квантовая частица имеет отличную от нуля ве­роятность прохождения сквозь потенциальный барьер конечной ширины (туннельный эффект).

Для описания туннельного эффекта вводится понятие коэффициента прозрачности потенциального барьера D, который определяется отношением плотности потока прошед­ших частиц к плотности потока падающих. Как показывают рас­четы, коэффициент прозрачности потенциального барьера D зави­сит от высоты U и ширины ℓ по­тенциального барьера, энергии Е и массы m частицы:

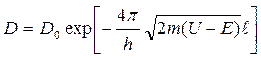(26.31)

[D₀ — постоянный множитель].

С классической точки зрения прохождение частицы сквозь потенци­альный барьер при Е<U противоречит закону сохранения энергии. Дело в том, что если классическая частица находилась бы в какой-то точке в области барьера, то ее полная энергия оказалась бы меньше ее потенци­альной энергии, что абсурдно. С квантовой точки зрения такого противо­речия нет. Если частица движется к барьеру, то до столкновения с ним она имеет вполне определенную энергию. Если взаимодействие с барье­ром длится в течение времени Δt, то, согласно соотношению неопреде­ленностей, энергия частицы в состоянии взаимодействия с барьером уже не будет определенной, а характеризуется неопределенностью

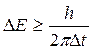(26.32)

Если эта неопределенность порядка высоты барьера, то он пе­рестает быть для частицы непреодолимым препятствием и частица «пройдет» сквозь него.

Основы теории туннельных переходов заложены работами физиков во главе с Л.И. Мандельштамом. Туннельное прохождение сквозь потен­циальный барьер лежит в основе многих явлений физики твердого тела (например, явления в контактном слое на границе двух полупроводни­ков), атомной и ядерной физики (например, α-распад, протекание термо­ядерных реакций).

 

⇐ Предыдущая12345

Поделиться:

Воспользуйтесь поиском по сайту: