 |
Особенности количественной оценки надежности невосстанавливаемых объектов
|
|
|
|
Одним из основных показателей надежности (количественной мерой надежности) является вероятность безотказной работы (ВБР) - вероятность того, что в пределах заданной наработки отказ объекта не возникает.
Вероятность безотказной работы является функцией времени и выражает вероятность того, что случайное время работы объекта до отказа  будет больше заданной наработки
будет больше заданной наработки  , отсчитываемой от начала эксплуатации или восстановления, т.е.
, отсчитываемой от начала эксплуатации или восстановления, т.е.
 (1)
(1)
Эту функцию часто называют функцией надежности.
Таким образом, в теории надежности рассматриваются случайное событие – возникновение отказа и случайная величина - время безотказной работы.
Свойства функции  :
: 
1.  , т.е. в начальный момент эксплуатации объект находится в работоспособном состоянии.
, т.е. в начальный момент эксплуатации объект находится в работоспособном состоянии.
2.  т.е.
т.е.  - монотонно убывающая функция.
- монотонно убывающая функция.
3.  , т.е. любой технический объект со временем откажет.
, т.е. любой технический объект со временем откажет.
Наряду с вероятностью безотказной работы используется понятие вероятность отказа, т.е. вероятность того, что объект откажет в пределах заданной наработки, будучи работоспособным в начальный момент времени. Иначе говоря, вероятность отказа есть вероятность того, что время безотказной работы  будет меньше заданной наработки
будет меньше заданной наработки  :
:
 (2)
(2)
Функция  является с точки зрения теории вероятностей функцией распределения случайной величины
является с точки зрения теории вероятностей функцией распределения случайной величины  (в теории вероятностей она обозначается как
(в теории вероятностей она обозначается как  .
.
Очевидно, что  .
.
На рис. 3 приведены графики возможных видов функций  и
и 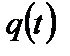 .
.

Рис.3. Графики функций  ,
, 
В ряде случаев представляет интерес не безотказная работа системы, а её способность сохранять способность к функционированию в процессе хранения в нерабочем состоянии. При этом вероятностный смысл характеристик надежности сохраняется полностью. В этом случае вместо термина ВБР используют термин ВСРС - вероятность сохранения работоспособного состояния.
|
|
|
Надежность элемента или системы не всегда удобно характеризовать вероятностью безотказной работы, т. к. для небольших значений наработки значения ВБР будут близкими к единице.
Например, ВБР слюдяного конденсатора в течение одного часа работы равна 0,9999999.
Поэтому наряду с ВРБ используются другие показатели, например, плотность распределения времени работы до отказа, которая является дифференциальной формой закона распределения наработки до отказа, то есть производной от функции распределения:
 . (3)
. (3)
 является неотрицательной функцией, причем
является неотрицательной функцией, причем
 .
.

Рис. 4. График функции 
Величина 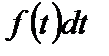 характеризует вероятность отказа за интервал наработки
характеризует вероятность отказа за интервал наработки  объекта, взятого наугад из множества одинаковых объектов.
объекта, взятого наугад из множества одинаковых объектов.
При этом неизвестно, работоспособен этот объект к началу интервала (в момент  ) или отказал ранее. Это не всегда удобно на практике, и
) или отказал ранее. Это не всегда удобно на практике, и  , как самостоятельный показатель надежности, находит ограниченное применение. Этот показатель применяется при теоретических исследованиях надежности. Чаще применяют такой показатель, как интенсивность отказов
, как самостоятельный показатель надежности, находит ограниченное применение. Этот показатель применяется при теоретических исследованиях надежности. Чаще применяют такой показатель, как интенсивность отказов  - условную плотность вероятности возникновения отказа объекта, определяемую при условии, что до рассматриваемого момента времени отказ не возник. Следует заметить одну характерную особенность. Мы говорим во множественном числе «интенсивность отказов», хотя речь идет о невосстанавливаемых технических объектах, то есть работающих до первого отказа, который является для них и последним. Дело в том, что говоря во множественном числе, мы имеем в виду, что речь идет о большой группе одинаковых объектов (в терминах теории вероятностей речь идет о генеральной совокупности). Но, естественно, каждый из этих невосстанавливаемых объектов отказывает только один раз. Интенсивность отказов имеет размерность «количество отказов в единицу времени». Для технических объектов, находящихся в работе, наиболее часто применяется размерность «количество отказов в час». Для объектов, находящихся в режиме хранения, обычно применяется размерность «количество отказов в год». Очевидно, чем меньше интенсивность отказов, тем надежнее техника.
- условную плотность вероятности возникновения отказа объекта, определяемую при условии, что до рассматриваемого момента времени отказ не возник. Следует заметить одну характерную особенность. Мы говорим во множественном числе «интенсивность отказов», хотя речь идет о невосстанавливаемых технических объектах, то есть работающих до первого отказа, который является для них и последним. Дело в том, что говоря во множественном числе, мы имеем в виду, что речь идет о большой группе одинаковых объектов (в терминах теории вероятностей речь идет о генеральной совокупности). Но, естественно, каждый из этих невосстанавливаемых объектов отказывает только один раз. Интенсивность отказов имеет размерность «количество отказов в единицу времени». Для технических объектов, находящихся в работе, наиболее часто применяется размерность «количество отказов в час». Для объектов, находящихся в режиме хранения, обычно применяется размерность «количество отказов в год». Очевидно, чем меньше интенсивность отказов, тем надежнее техника.
|
|
|
Как свидетельствует многолетний опыт эксплуатации различных технических объектов, интенсивность отказов имеет место не только при работе, но и при хранении в нерабочем состоянии. Безусловно, интенсивность отказов при хранении зависит от условий хранения. Очевидно, что хранение под открытым небом, приведет к большему числу отказов, чем хранение в закрытом помещении. Очевидно также, что интенсивность отказов при работе во много раз больше, чем при хранении. Можно привести такие цифры: по опыту эксплуатации отношение интенсивности отказов при работе к интенсивности отказов при хранении лежит в диапазоне 500…10000. Если говорить о корабельном вооружении, то левая часть диапазона относится к системам управления оружием, а правая часть к бортовой аппаратуре ракет. Но, конечно, для каждого комплекса оружия цифры будут разными. Их необходимо определять в процессе испытаний и эксплуатации. Знание интенсивности отказов при хранении позволяет, в частности, обосновать периодичность проверок технического состояния ракет при хранении их на базах вооружения.
В качестве показателя надежности неремонтируемых изделий применяется также такая характеристика, как математическое ожидание наработки объекта до отказа  . Индексом 1 принято обозначать объекты, работающие до первого отказа, то есть невосстанавливаемые объекты.
. Индексом 1 принято обозначать объекты, работающие до первого отказа, то есть невосстанавливаемые объекты.
Для невосстанавливаемых объектов в качестве показателя надежности применяется также коэффициент готовности, который представляет собой вероятность того, что в любой момент на интересующем нас интервале  объект будет работоспособен. Другими словами, коэффициент готовности представляет собой среднее значение вероятности безотказной работы объекта на интересующем нас временном интервале
объект будет работоспособен. Другими словами, коэффициент готовности представляет собой среднее значение вероятности безотказной работы объекта на интересующем нас временном интервале  .
.
Коэффициент готовности для группы однотипных технических объектов можно интерпретировать, как долю объектов, сохранивших работоспособное состояние на интересующем нас временном интервале  .
.
|
|
|
Перечисленные характеристики представляют практический интерес в том случае, если их можно оценить количественно, то есть, если имеются расчетные формулы. Рассмотрим вывод формулы для вероятности безотказной работы. Как было отмечено ранее, вероятность безотказной работы является функцией времени и выражает вероятность того, что случайное время работы объекта до отказа  будет не менее заданной наработки
будет не менее заданной наработки  , отсчитываемой от начала эксплуатации или восстановления, то есть:
, отсчитываемой от начала эксплуатации или восстановления, то есть:
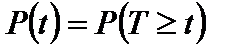
На практике чрезвычайно важно знать конкретный вид функции в правой части этой формулы, то есть расчетную формулу, по которой можно получить значение вероятности безотказной работы для любого времени  .
.
Очевидно, вероятность безотказной работы зависит от интенсивности отказов, которая в свою очередь является своеобразным ярлыком качества техники в смысле надежности. Часто именно интенсивность отказов определяет победу в борьбе за потребителя конкурирующих фирм. По определению интенсивность отказов представляет собой условную плотность вероятности возникновения отказа объекта, определяемую при условии, что до рассматриваемого момента времени отказ не возник, то есть:
 . (4)
. (4)
Условие, что до рассматриваемого момента  отказ не возник, определяется стоящей в знаменателе вероятностью безотказной работы
отказ не возник, определяется стоящей в знаменателе вероятностью безотказной работы  .
.
Используя это выражение, найдем связь вероятности безотказной работы с интенсивностью отказов.
Представим уравнение (4) в виде
 .
.
Решим это уравнение при начальном условии  .
.
Проинтегрируем левую и правую часть от 0 до  , в соответствии с определением вероятности безотказной работы. При этом, чтобы предел интегрирования не совпадал по обозначению с переменной интегрирования, обозначим её через x:
, в соответствии с определением вероятности безотказной работы. При этом, чтобы предел интегрирования не совпадал по обозначению с переменной интегрирования, обозначим её через x:
 ,
,
 .
.
Т.к. 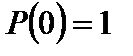 и
и  , то
, то

и, следовательно,
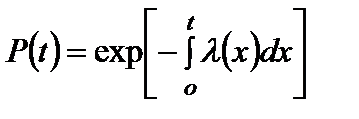 . (5)
. (5)
при  формула (5) примет вид
формула (5) примет вид
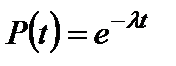 . (6)
. (6)
Эту формулу по праву часто называют основной формулой теории надежности или функцией надежности, поскольку на установившихся режимах эксплуатации интенсивность отказов близка к стационарной ( ), и расчет вероятности безотказной работы не составляет труда.
), и расчет вероятности безотказной работы не составляет труда.
|
|
|
В качестве показателя надежности часто используется ВБР в пределах заданной наработки. Это условная вероятность безотказной работы  в течение наработки от
в течение наработки от  до
до 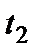 при условии, что в момент
при условии, что в момент  объект был работоспособным. Её можно определить следующим образом. Рассмотрим два интервала
объект был работоспособным. Её можно определить следующим образом. Рассмотрим два интервала  и
и  . Событие, состоящее в безотказной работе в течение интервала
. Событие, состоящее в безотказной работе в течение интервала  , является совмещением двух событий:
, является совмещением двух событий:
- объект безотказно проработал на интервале  ;
;
- оставшийся работоспособным к моменту  , объект безотказно проработал и на интервале
, объект безотказно проработал и на интервале  .
.
тогда
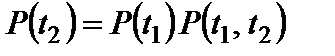 .
.
Отсюда
 . (7)
. (7)
Таким образом, условная вероятность безотказной работы на интервале  равна отношению значений ВБР в конце и в начале интервала:
равна отношению значений ВБР в конце и в начале интервала:
 , (8)
, (8)
при 
 . (9)
. (9)
Таким образом, при  вероятность безотказной работы элемента в интервале
вероятность безотказной работы элемента в интервале  не зависит от того, сколько времени элемент уже проработал, если к моменту времени
не зависит от того, сколько времени элемент уже проработал, если к моменту времени 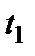 он был работоспособен. Эта вероятность зависит только от длины интервала.
он был работоспособен. Эта вероятность зависит только от длины интервала.
Говоря о таком показателе, как математическое ожидание времени работы до отказа, следует отметить, что в практике эксплуатации он используется чаще, чем вероятность безотказной работы. Этот показатель понятен даже специалистам невысокой квалификации. Действительно, когда мы говорим о количестве часов, в течение которых техника работает безотказно, комментариев не требуется. Для большинства законов распределения математическое ожидание представляет собой среднюю наработку до отказа, то есть, среднее арифметическое времени работы до отказа для генеральной совокупности группы однотипных невосстанавливаемых элементов.
Среднюю наработку до отказа  вычисляют по формуле теории вероятностей для непрерывных случайных величин:
вычисляют по формуле теории вероятностей для непрерывных случайных величин:
 . (10)
. (10)
Интегрируя по частям, получаем:
 .
.
можно показать, что
 .
.
тогда средняя наработка до отказа
 , (11)
, (11)
т.е. она численно равна площади под кривой  .
.
При 
 . (12)
. (12)
Таким образом, в случае  математическое ожидание времени работы до отказа и интенсивность отказов обратно пропорциональны. Зная одну из этих двух характеристик, можно определить другую.
математическое ожидание времени работы до отказа и интенсивность отказов обратно пропорциональны. Зная одну из этих двух характеристик, можно определить другую.
Подставив значение  в формулу вероятности безотказной работы, получим, что при
в формулу вероятности безотказной работы, получим, что при 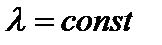 среднюю наработку до отказа можно понимать как наработку
среднюю наработку до отказа можно понимать как наработку  , в течение которой объект остается работоспособным с вероятностью
, в течение которой объект остается работоспособным с вероятностью 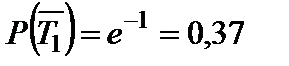 и, следовательно, откажет в течение времени
и, следовательно, откажет в течение времени  с вероятностью равной 0,63. То есть, следует иметь в виду, что вероятность того, что объект проработает безотказно в течение времени, равном математическому ожиданию времени его безотказной работы равна лишь 37 %. Это нужно учитывать на практике.
с вероятностью равной 0,63. То есть, следует иметь в виду, что вероятность того, что объект проработает безотказно в течение времени, равном математическому ожиданию времени его безотказной работы равна лишь 37 %. Это нужно учитывать на практике.
|
|
|
Говоря о вычислении коэффициента готовности, следует иметь в виду, что он численно равен среднему значению вероятности безотказной работы объекта на интересующем нас временном интервале  . Таким образом, очевидно, что для определения коэффициента готовности необходимо площадь под кривой функции надежности разделить на длину интервала
. Таким образом, очевидно, что для определения коэффициента готовности необходимо площадь под кривой функции надежности разделить на длину интервала  :
:
 (13)
(13)
учитывая, что:
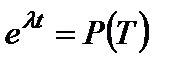 и
и 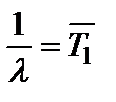 ,
,
получим:  . С учетом, что
. С учетом, что  ,
,
окончательно получим:
 . (14)
. (14)
На практике часто рассмотренные ранее характеристики надежности для исследуемых объектов неизвестны. Особенно это справедливо для технических объектов новых типов, разработанных на основе новой элементной базы. Но, конечно, персоналу, эксплуатирующему технику, важно знать эти характеристики. Тогда будет возможно прогнозировать возможные отказы и планировать техническое обслуживание.
Для получения статистических оценок характеристик надежности организуются специальные испытания, либо ведется наблюдение за группой однотипных элементов, находящихся в эксплуатации.
В качестве исходной информации при расчете статистических оценок характеристик надежности используются:
 - число работоспособных объектов при
- число работоспособных объектов при  ;
;
 - число объектов, отказавших на интервале времени
- число объектов, отказавших на интервале времени  ;
;
 - число объектов, отказавших на интервале времени
- число объектов, отказавших на интервале времени  ;
;
 - наработка до отказа каждого из объектов.
- наработка до отказа каждого из объектов.
Статистические оценки характеристик надежности определяются по следующим формулам математической статистики:
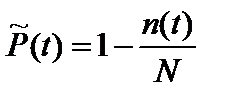 ; (15)
; (15)
 ; (16)
; (16)
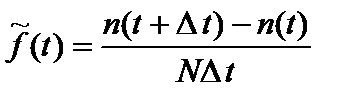 ; (17)
; (17)
 ; (18)
; (18)
 . (19)
. (19)
Для наиболее точного определения  все
все  объектов испытываются до отказа.
объектов испытываются до отказа.
|
|
|


