 |
Методы расчета необходимого количества запасных частей на период эксплуатации техники
|
|
|
|
Допустим, в рассматриваемом техническом устройстве функционирует некоторое количество элементов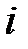 
-го типа 
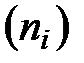и в составе ЗИП имеется 
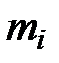элементов того же типа. Поскольку число элементов 
-го типа в запасе ограничено, а число отказов элементов 
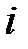-го типа в системе за время эксплуатации 
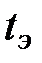может быть достаточно большим, то, очевидно, будет существовать вероятность 
того, что отказов элементов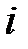 
-го типа 
будет больше, чем количество запасных элементов в ЗИПе. Если при очередном отказе элемента в рассматриваемой системе будет обнаружено отсутствие необходимого запасного элемента, то эксплуатация системы прекращается, т.к. восстановление отказавшего устройства становится невозможным. Таким образом, необходимо обосновывать объем заказов запасных частей каждого типа на предстоящий период эксплуатации.
Наиболее приемлемой характеристикой для оценки влияния объема заказов на эксплуатационные показатели будет принято считать уровень гарантии функционирования системы 
. По смыслу, уровень гарантии функционирования есть вероятность того, что число отказов в системе за некоторый период времени не превысит числа имеющихся запасных элементов, т.е., вероятность того, что в комплекте ЗИП в случае необходимости всегда будет запасной элемент.
Скажем, для элементов 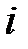-го типа, работающих в системе, уровень гарантии функционирования
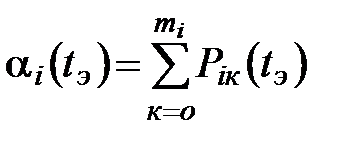, (52)
где: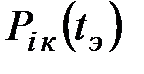 
- вероятность появления в системе ровно 
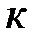отказов элементов 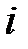-го типа за время эксплуатации 
;
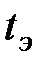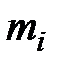- количество запасных элементов 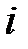-го типа.
Установлено, что поток отказов имеет распределение Пуассона. Вспомним формулу распределения Пуассона:
.
Эта формула определяет вероятность появления ровно к интересующих нас случайных событий на определенном временном интервале, если известно математическое ожидание (МО) количества этих событий на этом интервале. Запишем эту формулу в несколько измененном виде, имея в виду поток отказов при эксплуатации вооружения.
|
|
|
Если поток отказов элементов 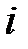-го типа простейший 
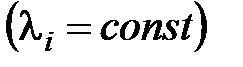и общее количество элементов в системе 
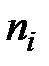, то формула распределения Пуассона примет вид: 
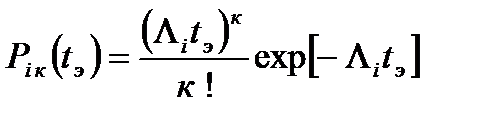, (53)
где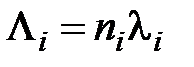 
- поток отказов совокупности элементов 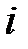-го типа, а произведение 
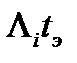представляет собой математическое ожидание количества отказов за время эксплуатации .
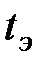Тогда уровень гарантии функционирования (формула 52) запишется в виде: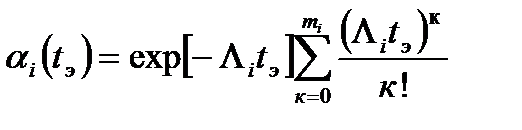 
. (54)
Значение к=0 означает отсутствие запасных частей данного типа, к=1 означает наличие одной запасной части и т.д.
Необходимое количество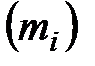 
элементов 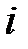-го типа в комплекте ЗИП найдется из соотношения
, (55)
где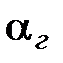 
- требуемые уровень гарантии функционирования (часто 
).
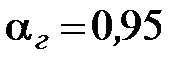При расчете больших объемов запасных частей, когда речь идет о многих сотнях и даже тысячах единиц, расчет по формуле (54) может вызвать затруднения из-за чрезвычайно больших значений факториала к!. В этом случае используется рекуррентное соотношение.
Если 
, то следующее значение вероятности будет равно:
. Таким образом, имеем: 
.
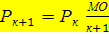Это рекуррентное соотношение позволяет определить очередной член последовательности вероятностей, зная предыдущий член и математическое ожидание количества отказов на интересующем нас интервале времени.
Расчет будет идти в следующей последовательности:
; 
; 
; 
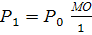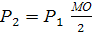и так далее.
При таком подходе не нужно рассчитывать факториалы больших чисел и опасаться «проклятия размерности». Рассчитанные в этой последовательности вероятности суммируются до тех пор, когда сумма не достигнет значения гарантированной вероятности и, значит, определится необходимое для этого количество запасных частей. Такой расчет удобно организовать с использованием вычислительной техники.
|
|
|
Определение потребного количества запасных частей можно производить и графическим способом.
Удобны для расчета графики 
(рис.21).
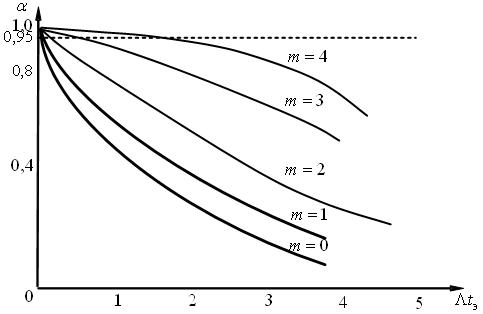
Рис.21. Зависимость вероятности сохранения работоспособности от математического ожидания числа отказов
Рассчитав математическое ожидание количества отказов (
) и исходя из гарантированной вероятности (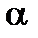
) с помощью графика определяется необходимое количество запасных частей (m).
Говоря об одиночном комплекте ЗИП, следует отметить, что в принципе одиночные комплекты иметь невыгодно, т.к. вероятность возникновения отказов на всех однотипных объектах за интересующий эксплуатационника период всегда меньше вероятности отказа одного или нескольких из этих объектов за тот же срок. То есть, требуемый уровень гарантии функционирования для нескольких систем можно обеспечить относительно меньшим количеством запасных элементов. Из графика видно, что темп нарастания потребного количества запасных элементов при заданном уровне гарантии функционирования отстает по сравнению с темпом нарастания параметра потока отказов. На практике одиночный комплект ЗИП необходим, т.к. объекты эксплуатации часто не имеют связи с базами снабжения. Аналитический расчет базируется на использовании формулы 54. При этом суммирование ведется до тех пор, пока не выполнится условие (формула 55). Значение 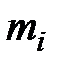, при котором выполняется это условие, и есть искомое количество запасных частей данного типа.
В состав группового комплекта ЗИП включаются, как правило, наиболее надежные элементы, которые в случае размещения их в одиночном комплекте ЗИП были бы, как правило, ненужным грузом. Кроме того, в групповой комплект включаются громоздкие, массивные блоки, размещение которых на объектах эксплуатации затруднительно, например, антенные посты. Нередко группой комплект создается для 8-10-ти однотипных технических систем если, конечно, такое их количество имеется в данном регионе. Расчет необходимого количества запасных частей в групповом комплекте производится по той же методике, что и расчет для одиночного комплекта. Безусловно, при этом учитывается общий поток отказов от всей группы однотипных комплексов вооружения. При этом отдельно рассчитываются комплекты ЗИП для работающей техники и техники, находящейся в режиме хранения, поскольку интенсивности отказов той и другой техники принципиально отличаются.
|
|
|
|
|
|
