 |
Расчет надежности с учетом структуры технической системы
|
|
|
|
Говоря о практическом значении теории надежности, следует отметить, что умение производить расчеты характеристик надежности технических систем с учетом их структуры является основной задачей на этапе проектирования и в процессе эксплуатации.
С точки зрения надежности все технические системы подразделяются на простые и сложные. Критерием при этом является работоспособность всей системы.
Простая, с точки зрения надежности, система - это такая система, в которой отказ хотя бы одного элемента приводит к отказу всей системы.
При расчетах обычно предполагается, что отказы элементов являются событиями независимыми. Учитывая это допущение, которое в конкретных случаях следует обосновывать, можно воспользоваться теоремой умножения вероятностей
(28)
где 
- ВБР системы;
- ВБР i - ого элемента системы;
n - число элементов системы, отказ любого из которых приводит к выходу из строя системы.
Учитывая, что 
уравнение (28) можно представить в виде
,
или
.
Обозначим
,
где 
- интенсивность отказов системы. равная сумме интенсивностей отказов отдельных элементов, т.е. это 
- характеристика системы.
Тогда 
.
При стационарном потоке отказов 
последняя формула примет простой вид
. (29)
При малых значениях показателя степени, используя разложение в ряд
и ограничиваясь двумя членами разложения (при 
ошибка не превышает 0,5%), представим формулу (29) в вице:
.
В случае, когда интенсивности отказов всех элементов не зависят от времени 
и система состоит из 
групп элементов, одинаковых в каждой группе
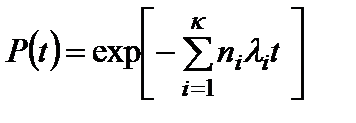, (30)
где 
- интенсивность отказов элементов i -ого типа;
- число элементов i -ого типа в группе;
к - количество групп однородных элементов.
|
|
|
Пример: В состав технического устройства входят элементы 3-х типов:n1 = 320шт.,n2 = 1560шт., n3 = 650шт.
Соответствующие интенсивности отказов:
; 
; 
.
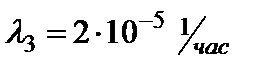Определить вероятность безотказной работы технического устройства в течение одного, десяти и ста часов непрерывной работы, считая техническое устройство с точки зрения надежности простой системой. Тогда
.
Подставив исходные данные, получим:
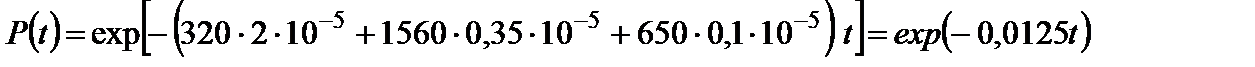Отсюда: 
Простые системы в чистом виде встречаются крайне редко. Они являются, как правило, фрагментами сложных систем.
Сложная, с точки зрения надежности, система - это такая система, в которой отказ одного или нескольких элементов, входящих в её состав, еще не приводит к отказу всей системы в целом.
Перед расчетом надежности определяется содержание термина "безотказная работа системы", рассматриваются условия функционирования системы с целью оценки влияния каждого элемента на ее работоспособность.
Затем составляется блок-схема надежности системы.
Сформулируем правила составления блок-схемы надежности:
1) Если работоспособность системы или ее части обеспечивается только совместной работой группы элементов, то такие элементы соединяются последовательно. То eсть, в простой, с точки зрения надежности, системе элементы соединяются последовательно;
2) Если работоспособность системы или ее части обеспечивается работой хотя бы одного элемента из группы, то такие элементы соединятся параллельно. Иначе: если только совместный отказ всех элементов группы приводит к отказу системы или ее части, то такие элементы соединять параллельно.
Рассмотрим метод расчета надежности сложных систем на примере. Допустим, в состав системы входят следующие восемь элементов: А, Б, В, Г, Д, Е, Ж, 3. Из анализа процесса функционирования системы выявились следующие комбинации элементов, которые, будучи работоспособными обеспечивают нормальную работу системы в целом: АБЖЗ, АВЖЗ, ГДЖЗ и ГЕЖЗ, т.е. безотказная работа системы обеспечивается, если исправны элементы: А и Б (или В), а также Ж и З или Г и Д (или Е), а также Ж и З.
|
|
|
Вместо этого словесного описания составим блок-схему надежности, где слову "и" соответствует последовательное соединение элементов, а слову "или" параллельное (рис.13).
Рис.13. Блок-схема надежности.
Блок-схема надежности состоит из комбинаций последовательно и параллельно соединенных элементов. В случае независимости отказов вероятность безотказной работы последовательно соединенных элементов равна произведению вероятностей безотказной работы отдельных элементов
,
а вероятность отказа параллельно соединенных элементов равна произведению вероятностей отказов отдельных элементов
.
Следовательно, ВБР параллельно соединенных элементов
. (31)
Приведенные соотношения позволяют рассчитать надежность сложной системы. Для упрощения расчетов целесообразно выделить в блок-схеме надежности подблоки. На рис.13 выделено три подблока: I, II, III. Подблоки образуют более простую систему, надежность которой определить сравнительно несложно, если известна надежность подблоков. Надежность же подблоков легко выразить через надежность исходных элементов. Для приведенной схемы
.
Надежность подблоков определится следующими формулами:
Подставив значения 
в формулу для вероятности безотказной работы системы (Р) получим:
При конкретных расчетах, очевидно, нецелесообразно записывать формулу в окончательном виде. Во избежание ошибок лучше производить расчеты в подблоках и подставлять в общую формулу уже числовые результаты.
Следует отметить, что блок-схемы надежности, хотя и строятся на базе принципиальных или функциональных схем, могут существенно отличаться от них. Например, два конденсатора, соединенных параллельно, на блок-схеме надежности должны быть изображены как два элемента, соединенных последовательно, т.к. пробой одного конденсатора исключает нормальную работу другого.
Принципиальная схема:
Схема надежности:
Комбинациями последовательно и параллельно соединенных элементов не исчерпываются возможные варианты блок-схем надежности сложных систем. В качестве примера рассмотрим мостиковую схему (рис.14а).
|
|
|
Указанную схему невозможно свести к комбинациям только последовательно и параллельно соединенных элементов и, следовательно, невозможно применить ранее рассмотренные простые формулы.
В этом случае используется метод разложения сложной структуры по «ключевым элементам» и расчет надежности производится с использованием формулы полной вероятности. Указанный метод сводится к следующему.
В исходной структуре обычно выбирается элемент с наибольшим числом прямых связей с другими элементами. При этом расчет получается наиболее простым. В данной структуре это элемент 5.
Рис. 14. Разложение мостиковой схемы на две составляющие схемы.
Рассматривается первая гипотеза - элемент 5 исправен. Вероятность этой гипотезы 
равна вероятности безотказной работы элемента 5, т.е. 
. В этом случае в месте расположения элемента 5 можно поставить жесткую связь (сделать замыкание) и мостиковая схема преобразуется в схему, изображенную на рис. 14б. Но к этой схеме необходимо присоединить элемент 5 с тем, чтобы учесть, что вероятность полученной преобразованной схемы должна умножаться на ВБР элемента 5.
Тогда условная вероятность безотказной работы мостиковой схемы при условии работоспособного состояния элемента 5:
.
Рассматривается вторая гипотеза - элемент 5 неисправен (находится в состоянии отказа). Вероятность этой гипотезы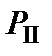 
равна вероятности отказа элемента 5, т.е. 
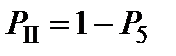. В этом случае в месте расположения элемента 5 делается обрыв и мостиковая схема с учетом вероятности отказа элемента 5 преобразуется в схему, изображенную на рис.14в.
Тогда условная вероятность безотказной работы мостиковой схемы при условии отказа элемента 5
Вероятность безотказной работы мостиковой схемы в соответствии с формулой полной вероятности определится суммой слагаемых (14б и 14в):
Приведенный метод является наиболее общим и пригоден для расчета надежности любых систем. В сложных случаях целесообразно применять его в несколько этапов. Следует заметить, что часто схемы бывают значительно сложнее, чем простая мостиковая, например, комбинация 2-х мостиковых. В этом случае количество ключевых элементов будет 2, а количество слагаемых в формуле полной вероятности 4, поскольку рассматриваются 4 варианта, а именно: 1)оба ключевых элемента работоспособны; 2)оба ключевых элемента отказали; 3)первый ключевой элемент работоспособен, а второй отказал; 4)первый ключевой элемент отказал, а второй – работоспособен. В общем случае количество слагаемых 
определяется по формуле:
|
|
|
,
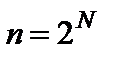где N – количество ключевых элементов. Основание 2 означает два возможных состояния ключевого элемента (отказал или работоспособен). Таким образом, в случае 3-х ключевых элементов количество слагаемых будет равно 8-ми.
Рассмотрим еще один вид схемы надежности, а именно, мажоритарное резервирование.
В различных технических системах применяются устройства, в которых имеются группы одинаковых элементов, выполняющих одну и ту же функцию. И если большинство этих элементов работоспособны, то принимается решение (часто автоматически) о правильной работе данного устройства. Такое резервирование называется мажоритарным. В качестве примера рассмотрим систему пожаротушения какого-либо объекта, например, погреба с ракетным боезапасом на корабле. В случае пожара в погребе создается исключительно опасная ситуация для корабля. Поэтому погреб должен быть оборудован высоконадежной системой пожаротушения. Для того, чтобы бороться с пожаром необходимо в первую очередь зафиксировать факт пожара. Для этого погреба оборудуются датчиками температуры и давления. Несмотря на высокую надежность этих датчиков, их устанавливают всегда несколько, в связи с важностью решаемой задачи. И если большинство этих датчиков сигнализируют о пожаре, то принимаются меры по тушению. В погреба подается забортная вода, вручную или автоматически. Таким образом, датчики включаются в схему мажоритарного резервирования. Рассмотрим в качестве примера мажоритарную схему из 3-х датчиков. Она срабатывает и выдает сигнал о пожаре в случае, если два или три датчика сигнализируют о критической ситуации в погребе. В случае срабатывания только одного датчика, вода в погреб не подается, поскольку это может быть ложным срабатыванием из-за отказа датчика. На рисунке 15 цифрами 1,2,3 обозначены датчики температуры, сигнализирующие о недопустимом её повышении. Часто такой температурой является 70 градусов по Цельсию. Пунктиром на схеме обозначен так называемый логический (мажоритарный) элемент (ЛЭ), состоящий из трех схем типа «И» и одной схемы типа «ИЛИ». Логический элемент находится вне зоны действия высоких температур.
|
|
|
Рис.15.Схема мажоритарного резервирования по принципу «два из трех».
Вероятность безотказной работы такой схемы зависит от надежности логического элемента и надежности системы датчиков. Будем считать надежность логического элемента заданной. Определим ВБР системы датчиков. Поскольку датчики одинаковые, то их ВБР тоже можно считать одинаковыми. Нас интересует безотказная работа хотя бы 2-х из 3-х датчиков.
В нашем случае речь идет о случайной дискретной величине – количестве работоспособных датчиков. Очевидно, возможно всего 4 варианта, а именно:
1) все три датчика работоспособны,
2) работоспособны только два (любых) датчика,
3) работоспособен только один (любой) из датчиков,
4) все три датчика отказали.
Налицо полная группа событий. Стало быть, сумма вероятностей этих событий равна 1. Система пожаротушения сработает только в случае реализации 1-го или 2-го вариантов. Вероятности этих вариантов мы и должны определить. В нашем случае имеет место биномиальное распределение, определяющее вероятности реализации того или иного варианта из 4-х. Согласно биномиальному распределению вероятность появления ровно k интересующих нас событий (работоспособных датчиков) из n возможных определяется по формуле:
,
где 
– количество сочетаний из 
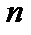по 
;
.
Очевидно, что число сочетаний из 3-х по 2 равно 3, а число сочетаний из 3-х по 3 равно1.
В формуле биномиального распределения р - вероятность безотказной работы каждого из n датчиков.
По этой формуле можно определить вероятность каждого из перечисленных вариантов. В нашей схеме мажоритарного резервирования нас интересует, очевидно, вероятность работоспособного состояния не менее 2-х датчиков. Эта вероятность, согласно биномиальному распределению будет равна сумме вероятности работоспособного состояния всех трех датчиков и вероятности работоспособного состояния двух датчиков из трех. Получив таким образом вероятность работоспособного состояния не менее 2- х датчиков и умножив её на ВБР логического элемента, мы получим ВБР схемы, обеспечивающей выдачу сигнала на подачу пламегасящего компонента к очагу пожара:
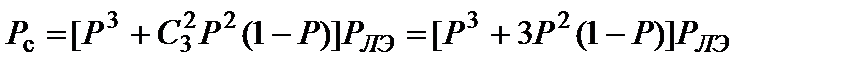. (32)
Следует заметить, что схемы мажоритарного резервирования могут строиться не только по принципу «два из трех». Встречаются, например, схемы типа «три из пяти», «четыре из семи» и другие. Но методика их расчета остается прежней.
|
|
|
