 |
Обратные задачи в теории надежности
|
|
|
|
Выше речь шла о так называемых «прямых» задачах, то есть, о таких, в которых по известной надежности элементов, составляющих техническую систему, определялась надежность всей системы.
На практике довольно часто решаются обратные задачи, когда заказчик ставит разработчику задачу обеспечить вероятность безотказной работы проектируемой технической системы не ниже какого-то конкретного значения. Рассмотрим некоторые типовые примеры обратных задач.
1.Требуется определить количество элементов, находящихся в «горячем» резерве для обеспечения заданной безотказности разрабатываемой технической системы.
Заметим, что «горячий» резерв - это такое соединение элементов, когда в случае отказа одного из них практически мгновенно его заменяет другой, то есть, это вариант параллельного резервирования.
Вероятность безотказной работы в случае параллельного соединения определяется по известной формуле:
.
Вероятность безотказной работы каждого элемента 
известна. Необходимо определить минимальное количество 
элементов для обеспечения заданной ВБР системы. Решая уравнение, найдем 
:
,
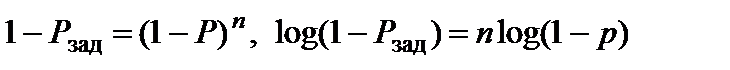отсюда,
.
Полученное по этой формуле значение округляется, естественно, в большую сторону до ближайшего целого числа.
2. Выработать требования к безотказности элементов, находящихся в «горячем» резерве, если по массогабаритным ограничениям разместить более какого-то их количества на объекте не представляется возможным. При этом, конечно, необходимо обеспечить ВБР разрабатываемой технической системы не ниже заданной.
Такая задача наиболее характерна для космической техники, где существуют жесткие ограничения по массе и габаритам.
|
|
|
Используя ту же исходную формулу, что и в предыдущей задаче, получим:
.
Разработчик должен найти элементы, обладающие надежностью не ниже рассчитанной. В конкурентной борьбе выживают те фирмы, которые выпускают лучшие, в смысле надежности, образцы техники.
3.Выработать требования к безотказности элементов, включенных в схему мажоритарного резервирования в целях обеспечения требуемой (заданной) вероятности безотказной работы всей схемы.
Рассмотрим в качестве примера схему, изображенную на рис.15.
Подобная схема характерна для систем пожаротушения важных объектов, например, хранилищ с ракетами. При срабатывании только одного датчика пламегасящая жидкость не должна подаваться в хранилище, так как это может быть ложным срабатыванием из-за отказа, и ракеты будут выведены из строя. Только при срабатывании большинства датчиков (2-х или 3-х) система пожаротушения вводится в действие. После небольших преобразований формулы 32 получим:
(33)
Таким образом, получено уравнение 3-ей степени относительно 
. В принципе подобные уравнения решаются с использованием формул Кардано. При этом из трех корней выбирается тот, значение которого лежит в диапазоне от 0 до 1, так как речь идет о вероятности. Хотя расчет несколько трудоёмок, но всё-таки возможен. Справедливости ради следует сказать, что в настоящее время существуют компьютерные программы решения уравнений третьей степени, но такой расчет можно выполнить лишь для простейшей мажоритарной схемы по принципу «два из трех». Если же схема будет посложнее, например, «три из пяти» или «четыре из семи», то аналитическое решение невозможно. И тогда на помощь приходит вычислительная техника. С её помощью решается прямая задача. Рассмотрим алгоритмический способ решения обратной задачи мажоритарного резервирования на примере схемы «два из трех» (рис. 15). Цикл решения заканчивается при выполнении условия, обозначенного в формуле 33. В представленном алгоритме в блок исходных данных вводятся: заданная вероятность безотказной работы системы пожаротушения (СП), вероятность безотказной работы логического (мажоритарного) элемента, начальное значение искомой вероятности безотказной работы 
каждого из датчиков температуры и шаг изменения этой вероятности. Обычно датчики обладают высокой надежностью, и исходное значение искомой вероятности принимается не ниже 0.9. Точность решения задачи определяется величиной шага приращения вероятности. Часто эта величина принимается равной 0.0001, так как нередко значение вероятности записывается в процентах с точностью до сотых долей.
|
|
|
Таким образом, решая с помощью ЭВМ прямую задачу, мы находим решение для обратной задачи. При этом степень уравнения не имеет значения.
Рис. 16. Блок-схема решения обратной задачи мажоритарного резервирования.
На этапе транспортирования, который характерен для большинства технических объектов, вероятность сохранения работоспособного состояния может быть уточнена с учетом возможных отказов в процессе транспортирования. Это, например, важно делать на этапе подачи боекомплекта ракет на корабль-носитель.
Для этого нужно вести учет отказов в процессе транспортирования. Вероятность работоспособного состояния ракеты после транспортирования можно представить выражением:
, (50)
где: 
— вероятность работоспособного состояния ракеты после транспортирования;
- интенсивность отказов на 1 километр пути (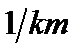
);
- дальность транспортирования (
).
зависит от вида транспорта (поезд, автомобиль, самолёт, корабль) и типа дороги в случае автомобильного транспорта (грунт, асфальт). Для расчета допустимой дальности транспортирования при заданной вероятности 
, формула (33) после простого преобразования превращается в следующее выражение:
(51)
назначается, исходя из обеспечения заданной боеготовности. Таким способом можно определить максимально допустимую дальность 
размещения технической базы вооружения от мест базирования кораблей-носителей. Если недостаточна статистика по отказам образцов оружия нового типа, то целесообразно проводить расчеты с использованием имеющихся статистических данных об оружии других типов в случае одинаковой элементной базы.
|
|
|
В том случае, если разместить техническую базу на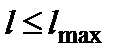 
не удаётся по каким-либо причинам (рельеф местности, близость других важных объектов и пр.), то следует улучшать условия транспортирования (строительство новых современных дорог, совершенствование транспортных средств). В этом случае уменьшится 
и, соответственно, можно будет увеличить дальность расположения технической базы от мест базирования кораблей-носителей.
|
|
|
