Следствия второго начала термостатики. Принцип существования энтропии.

Следствия второго начала термостатики широко применяются в термодинамических расчетах и формулируются на основе анализа его математического выражения (24), (25).

Следствие I. Совместное выражение первого начала термодинамики и второго начала термостатики позволяет получить дифференциальное уравнение термодинамики, которое связывает между собой все термодинамические свойства веществ

 

T ds= c_v dT + 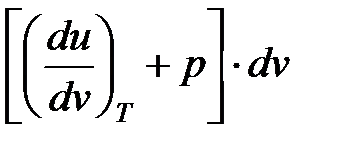 = c_p dT + .          (26)

 

Следствие II. Координаты Т - S являются универсальными координатами термодинамического теплообмена.

Рассмотрим процесс 1-2 в координатах Т-S и выделим на нем элементарный участок с температурой Т и изменением энтропии dS (рис. 5. ).

 

Рис. 5. Термодинамический процесс в координатах T-S

 

 

Исходя из математического выражения второго начала термостатики площадь под кривой элементарного участка процесса равна подводимому (отводимому) количеству теплоты

 

dQ = T× dS.                                            (27)

 

При этом полное количество теплоты, подведенной или отведенной от системы в процессе 1-2, определяется следующим образом:

 

Q_{1, 2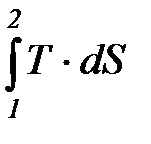} = .                                          (28)

 

Если из-под знака интеграла в соотношении (28) вынести среднюю температуру конечного процесса T_m , то количество теплоты в процессе может быть определено по соотношению

 

Q_{1, 2} = T_m× (S₂ - S₁).                                    (29)

 

Как видно из выражения (29) и рис. 6, знак теплообмена определяется знаком изменения энтропии. Процессы, протекающие с увеличением энтропии, сопровождаются подводом теплоты. Процессы, протекающие с уменьшением энтропии - отводом теплоты. Независимо от природы рабочего тела площадь под кривой процесса в координатах Т-S равна количеству подведенной или отведенной теплоты.

 

 

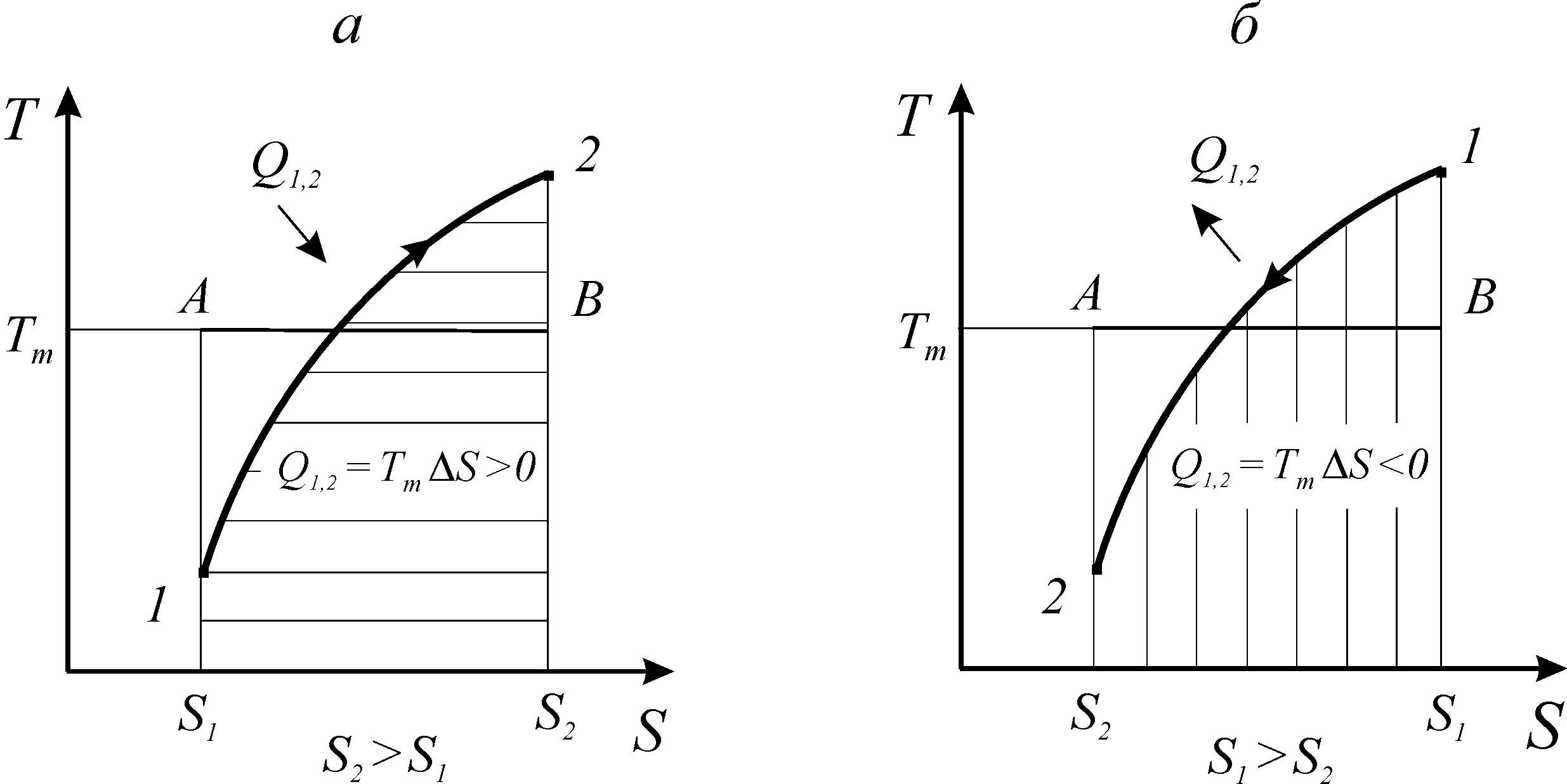
Рис. 6. Теплообмен в термодинамических процессах

 

Следствие III. Адиабатный процесс является процессом изоэнтропийным.

Так как в адиабатном процессе теплообмен отсутствует (dQ = 0), то, согласно второму началу термостатики (24), в таком процессе изменение энтропии dS = 0 (S = idem). Согласно этому следствию, показатель адиабатного процесса ( ) равен показателю изоэнтропийного процесса ( )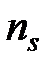

 

.                                                (30)

 

Следствие IV. Коэффициент полезного действия и холодильный коэффициент термодинамических циклов тепловых машин не зависят от вида цикла и природы рабочего тела, а определяются лишь средними абсолютными температурами рабочего тела в процессах подвода и отвода теплоты.

Рассмотрим термодинамические циклы в координатах Т-S: прямой цикл (цикл теплового двигателя) 1-А-2-В-1 (а) и обратный цикл (цикл холодильной машины) 1-А-2-B-1 (б) (рис. 7).

В процессе 1-А-2 теплота подводится к рабочему телу. Количество подводимой теплоты соответствует на диаграмме горизонтально заштрихованной площади. Вертикально заштрихованная площадь соответствует количеству отведенной теплоты от рабочего тела в процессе 2-В-1.

 

 

Рис. 7. Прямой и обратный циклы в координатах Т-S

 

Средние температуры рабочего тела в процессах подвода и отвода
теплоты в цикле теплового двигателя обозначим  Т_m1  и  Т_m2  
соответственно (рис. 7а). Согласно выражения (29), количества подведенной и отведенной теплоты определяется по следующим соотношениям:

 

                      ú Q₁ç = 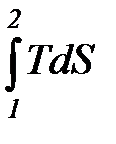 = T_m1 × ( S₂ - S₁ ) = T_m1 × ú DS_{1, 2}ç;                   (31)

 

                      ú Q₂ç =  = T_m2× × ( S₂ - S₁ ) = T_m2 × ú DS_{1, 2}ç,                     (32)

 

а коэффициент полезного действия любого термодинамического цикла теплового двигателя может быть найден из выражения

 

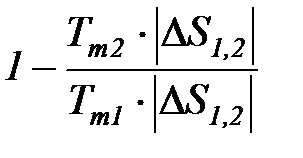= =1 - 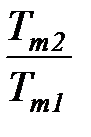.                      (33)

 

В результате аналогичных рассуждений получаем выражение для определения холодильного коэффициента термодинамического цикла холодильной машины (рис. 7б)

 

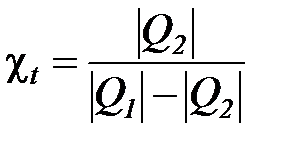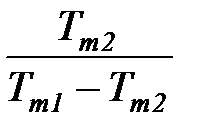 =  = .         (34)

 

Полученные выражения (33), (34) свидетельствуют о том, что КПД и холодильный коэффициент термодинамических циклов тепловых машин определяются только средними абсолютными температурами рабочего тела в процессах подвода и отвода теплоты.

Из уравнений (33), (34) следует также, что для любого термодинамического цикла тепловых машин выполняется следующее соотношение:

 

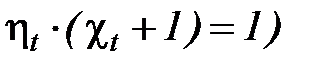.                                         (35)

Следствие V. Коэффициент полезного действия и холодильный коэффициент цикла Карно всегда выше этих коэффициентов эффективности для любых других термодинамических циклов тепловых машин, осуществляемых в одинаковом диапазоне предельных температур рабочего тела ( ).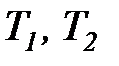

Это следствие вытекает из анализа соотношений по определению КПД цикла Карно и любого термодинамического цикла (33) теплового двигателя. Вследствие того, что Т₁ > Т_m1 и  Т₂ < Т_m2 (рис. 7а),

 

.                                            (36)

 

Аналогичный вывод можно сделать и при сравнении холодильных коэффициентов обратных циклов

 

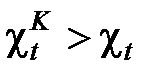.                                           (37)

 

Рассматриваемое следствие утверждает, что цикл Карно является эталонным циклом, по сравнению с которым можно определить термодинамическое совершенство любого цикла, осуществляемого в заданном интервале предельных значений температур рабочего тела.

Следствие VI. Изменение энтропии системы равно сумме изменений энтропии всех тел, входящих в систему (теорема аддитивности энтропии).

Количество теплоты, полученное в элементарном процессе системой, состоящей из 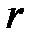 тел, можно определить из соотношения

 

,                                     (38)

 

что и подтверждает справедливость сформулированного следствия

 

.                     (39)

 

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: