Коэффициент теплопроводности. Дифференциальное уравнение теплопроводности

Коэффициент теплопроводности

Под коэффициентом теплопроводности понимают тепловой поток, передаваемый через единичную площадь поверхности при единичном значении температурного градиента

.                                           (11)

 

Коэффициент теплопроводности для каждого тела имеет свое численное значение и зависит от природы тела, пористости, влажности, давления, температуры и других параметров. Соотношение для определения теплового потока (7) получено при условии, что  не зависит от температуры, и является постоянной величиной. Однако, как показывают опыты, с достаточной для практики степенью точности, зависимость коэффициента теплопроводности от температуры для многих материалов можно принять линейной во всем рассматриваемом интервале температур

 

                                       (12)

 

где – коэффициент теплопроводности при температуре 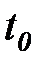; b – постоянная, характеризующая приращение (уменьшение)  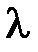материала при повышении его температуры на 1 градус.

Наихудшими проводниками теплоты являются газы. Коэффициент теплопроводности газов возрастает с увеличением температуры и изменяется в пределах 0, 005 ÷ 0, 5 Вт/(м·К).

Коэффициент теплопроводности жидкостей лежит в пределах
0, 07 ÷ 0, 7 Вт/(м·К) и, как правило (за исключением воды и глицерина), уменьшается с увеличением температуры.

Наилучшими проводниками теплоты являются металлы, у которых коэффициент теплопроводности изменяется в диапазоне  Вт/(м·К). У большей части чистых металлов с возрастанием температуры он уменьшается.

 

Дифференциальное уравнение теплопроводности

Распределение температуры в теле описывается дифференциальным уравнением теплопроводности. При условиях, что тело однородно и изотропно, физические параметры тела постоянны во времени и пространстве, температурные деформации рассматриваемого элементарного объема малы по сравнению с самим объемом, внутренние источники теплоты распределены в рассматриваемом объеме равномерно, макрочастицы тела неподвижны относительно друг друга, дифференциальное уравнение теплопроводности имеет следующий вид:

 

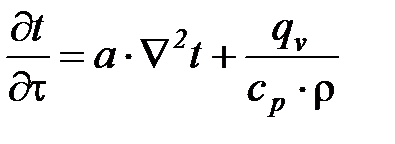
,               (13)

 

где  – коэффициент температуропроводности, характеризующий скорость изменения температуры в любой точке тела, м²/c;  – изобарная теплоемкость тела, ;  – плотность тела, кг/м³;  – объемная плотность внутренних источников теплоты, Bm/м³;  – оператор Лапласа.

           В цилиндрических координатах дифференциальное уравнение теплопроводности может быть представлено в следующей форме:

 

,                   (14)

 

где 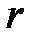 – радиус-вектор;  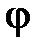– угол наклона радиуса-вектора.

Чтобы получить решение уравнения (13) для конкретного случая, необходимо описать особенности рассматриваемого процесса теплопроводности. Эти особенности называются условиями однозначности, включающими:

• геометрические условия (форма, размеры тела);
• физические условия (физические свойства тела и его параметры);
• начальные условия (распределение температуры в теле в начальный момент времени);
• граничные условия, определяющие взаимодействие тела с окружающей средой.

Граничные условия первого рода. Задается распределение температуры на поверхности тела, как функция координат и времени

                                             (15)

 

где 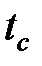 - температура поверхности тела.

В простейшем случае, если температура поверхности тела постоянна, выражение (15) имеет вид .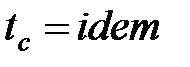

Граничные условия второго рода. Задается распределение плотности теплового потока на поверхности тела, как функция координат и времени

 

.                                            (16)

 

В частном случае, когда плотность теплового потока на поверхности тела остается постоянной, имеем .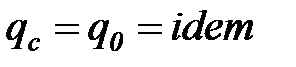

Граничные условия третьего рода. Задается температура окружающей среды 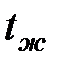 и закон теплообмена между поверхностью тела и окружающей средой (уравнение Ньютона-Рихмана)

 

 если 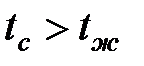,                              (17)

 

где 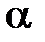– коэффициент теплоотдачи, Вm/(м²·К).

Тепловой поток, подведенный к поверхности тела, распространяется в теле по закону Фурье. Следовательно, на основании уравнений (8) и (17) имеем

,                                   (18)

где – температурный градиент у поверхности тела.

Выражение (18) можно записать в виде

 

.                                     (19)

 

Уравнение (19) является аналитическим выражением граничных условий третьего рода.

Граничные условия четвертого рода. Отражают условия теплообмена между телами, имеющими идеальный контакт и различные значения коэффициентов теплопроводности. При этих условиях и постоянном тепловом потоке, выражение граничных условий четвертого рода можно представить в виде

,                                    (20)

 

где 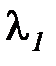,  – коэффициенты теплопроводности первого и второго тела, соответственно.

 

⇐ Предыдущая23242526272829303132Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: