 |
Теплопроводность плоской стенки
|
|
|
|
Теплопроводность плоской стенки
При установившемся (стационарном) тепловом режиме  и уравнение (13) принимает вид
и уравнение (13) принимает вид
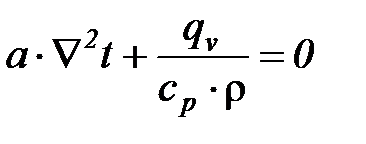 или
или  . (21)
. (21)
Развернутая форма оператора  зависит от выбранной системы координат. При отсутствии внутренних источников теплоты
зависит от выбранной системы координат. При отсутствии внутренних источников теплоты  дифференциальное уравнение теплопроводности при стационарном температурном поле запишется в следующем виде
дифференциальное уравнение теплопроводности при стационарном температурном поле запишется в следующем виде
 . (21а)
. (21а)
Определим тепловой поток через изотропную плоскую стенку. Предполагая, что температура меняется только в направлении, перпендикулярном плоскости стенки (рис. 2а), имеем:
 (22)
(22)
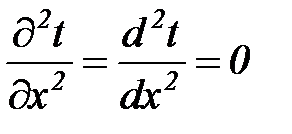 . (22а)
. (22а)
| б |
| а |

Рис. 2. Теплопроводность плоской однослойной (а) и многослойной (б)
стенки
Интегрируя уравнение (22а), имеем
 . (23)
. (23)
Второе интегрирование дает
 . (24)
. (24)
Постоянные интегрирования определяются из граничных условий первого рода:
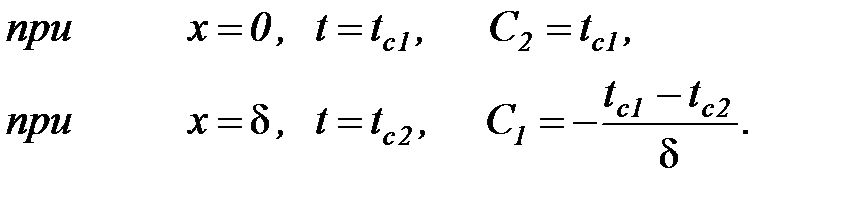 (25)
(25)
Подставляя постоянные интегрирования в соотношение (24), получим уравнение распределения температуры в плоской стенке
 . (26)
. (26)
Из выражения (26) следует, что температура в плоской стенке изменяется по линейному закону.
Из закона Фурье (8), с учетом формул (23) и (25), получаем уравнение теплопроводности через однослойную плоскую стенку
 . (27)
. (27)
Тепловой поток при теплопроводности через однослойную плоскую стенку определяется следующим образом:
|
|
|
 . (28)
. (28)
Отношение  называется тепловой проводимостью плоской стенки. Обратная величина
называется тепловой проводимостью плоской стенки. Обратная величина  представляет собой удельное термическое сопротивление плоской стенки.
представляет собой удельное термическое сопротивление плоской стенки.
Уравнения (27) и (28) могут быть представлены в виде:
 , (29)
, (29)
 . (30)
. (30)
Таким образом, можно утверждать, что значения удельного или полного теплового потока зависят от термического сопротивления стенки.
Рассмотрим процесс передачи теплоты теплопроводностью через плоскую трехслойную стенку (рис. 2б) при условиях, что толщина слоев стенки составляет 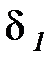 ,
, 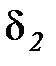 ,
, 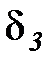 ; коэффициенты теплопроводности материалов слоев равны соответственно
; коэффициенты теплопроводности материалов слоев равны соответственно  ,
,  ,
,  ; контакт между стенками идеальный и температура на границе смежных слоев одинакова. Перенос теплоты происходит в стационарных условиях – значения плотности теплового потока через все слои стенки имеет одно и то же значение (q = idem).
; контакт между стенками идеальный и температура на границе смежных слоев одинакова. Перенос теплоты происходит в стационарных условиях – значения плотности теплового потока через все слои стенки имеет одно и то же значение (q = idem).
Запишем выражения плотности теплового потока через стенки и приравняем их, т. к. q = idem
 . (31)
. (31)
Выделим из соотношения (31) разности температур на каждом из слоев стенки:
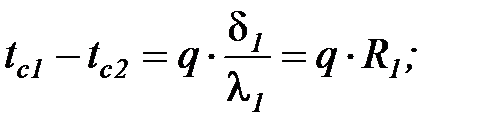 (32)
(32)
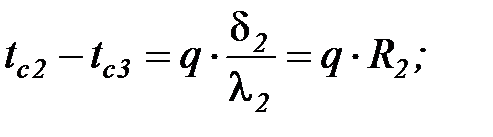 (32а)
(32а)
 (32б)
(32б)
Суммируя, левые и правые части уравнений (32), (32а), (32б), получаем: слева - изменение температуры в стенке 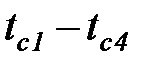 , справа – произведение плотности теплового потока q на сумму термических сопротивлений стенок
, справа – произведение плотности теплового потока q на сумму термических сопротивлений стенок 
 (33)
(33)
Таким образом, для определения плотности теплового потока через плоскую трехслойную стенку получим следующее выражение:
 (34)
(34)
В случае многослойной плоской стенки, состоящей из n слоев, выражение для плотности теплового потока может быть представлено в следующем виде:
|
|
|
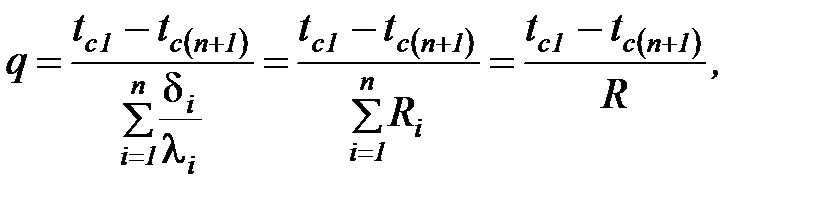 (35)
(35)
где R – общее термическое сопротивление многослойной плоской стенки.
Как следует из соотношения (35), плотность теплового потока прямо пропорциональна разности температур  и обратно пропорциональна термическому сопротивлению стенки R.
и обратно пропорциональна термическому сопротивлению стенки R.
Теплопроводность цилиндрической стенки
Рассмотрим процесс передачи теплоты теплопроводностью через цилиндрическую однослойную стенку (рис. 3) с внутренним диаметром d1=2r1 и наружным диаметром d2=2r2 в условиях стационарного температурного поля  . Внутренние источники теплоты отсутствуют (qv=0).
. Внутренние источники теплоты отсутствуют (qv=0).
Дифференциальное уравнение теплопроводности через цилиндрическую стенку (14) в рассматриваемых условиях имеет следующий вид:
 = 0. (36)
= 0. (36)

Рис. 3. Теплопроводность цилиндрической стенки
Температуры на наружной и внутренней поверхности цилиндрической стенки и по оси z, совпадающей с осью цилиндра, не изменяются:
 ;
; 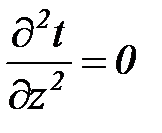 . (36а)
. (36а)
При данных условиях температура изменяется только по радиусу и дифференциальное уравнение теплопроводности принимает следующий вид:
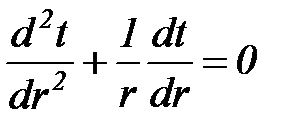 . (37)
. (37)
Граничные условия:
при  , (38)
, (38)
при  . (38а)
. (38а)
Для решения уравнения (37) введем новую переменную  , тогда уравнение (37) запишется в виде
, тогда уравнение (37) запишется в виде
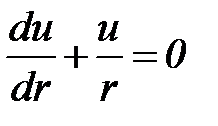 . (39)
. (39)
Интегрируя соотношение (39), получим
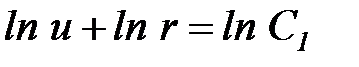 . (40)
. (40)
Потенцируя выражение (40) и переходя к первоначальным переменным, получаем
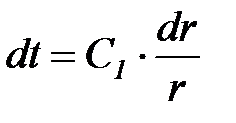 . (41)
. (41)
После интегрирования имеем
 . (42)
. (42)
Постоянные интегрирования С1 и С2 можно определить из граничных условий (38), (38а):
 ;
; 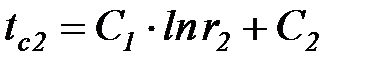 . (43)
. (43)
Решая систему уравнений (43) относительно С1 и С2, найдем:
 ;
; 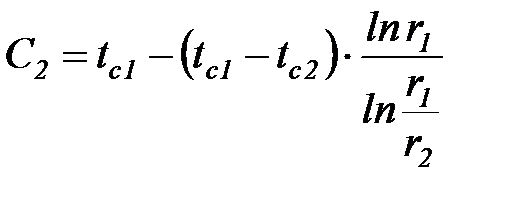 . (43а)
. (43а)
Подставляя полученные значения С1 и С2 в уравнение (42), получаем
 . (44)
. (44)
|
|
|
Уравнения температурного поля цилиндрической стенки (44) представляет собой уравнение логарифмической кривой.
То обстоятельство, что распределение температуры в цилиндрической стенке является криволинейным, можно объяснить тем, что плотность теплового потока через любую изотермическую поверхность будет величиной переменой, так как при неизменном тепловом потоке величина площади поверхности теплообмена зависит от радиуса.
Для определения теплового потока через цилиндрическую стенку воспользуемся законом Фурье
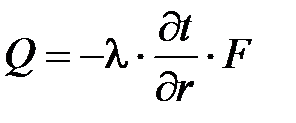 . (45)
. (45)
Подставляя в соотношение (45) значение градиента температуры (41) получим (учитывая, что  ) выражение для теплового потока через цилиндрическую стенку
) выражение для теплового потока через цилиндрическую стенку
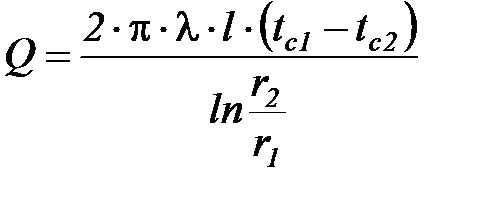 (46)
(46)
или
 . (46а)
. (46а)
Тепловой поток может быть отнесен либо к единице внутренней или внешней поверхности, либо к единице длины.
Тепловой поток через единицу площади внутренней поверхности находится из соотношения
 , (47)
, (47)
Тепловой поток через единицу площади внешней поверхности
 . (48)
. (48)
Тепловой поток через единицу длины цилиндрической стенки определяется по соотношению
 . (49)
. (49)
называется линейным тепловым потоком и имеет размерность Вm/м.
Рассуждая аналогично, как при получении расчетного соотношения теплового потока для многослойной плоской стенки, можно получить выражение для определения линейного теплового потока в случае многослойной цилиндрической стенки
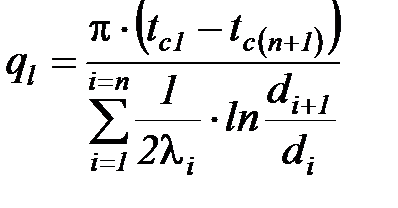 , (50)
, (50)
где величина 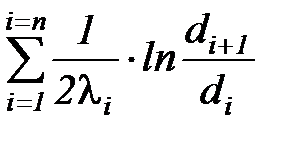
 называется линейным термическим сопротивлением теплопроводности многослойной цилиндрической стенки.
называется линейным термическим сопротивлением теплопроводности многослойной цилиндрической стенки.
Из уравнения (50) может быть определена температура на границе любых двух слоев
 , (51)
, (51)
где  – температура на границе i-го и (i+1)-го слоев цилиндрической стенки.
– температура на границе i-го и (i+1)-го слоев цилиндрической стенки.
|
|
|
|
|
|


