 |
Критерии подобия и критериальные уравнения
|
|
|
|
Критерии подобия и критериальные уравнения
Рассмотрим безразмерные комплексы величин, входящие в дифференциальные уравнения конвективного теплообмена (98) – (102):
(104)
Безразмерные комплексы, составленные из размерных величин, называются критериями подобия. Критерии подобия, составленные из известных величин, входящих в дифференциальные уравнения и условия однозначности, называются определяющими критериями.
Искомая величина - коэффициент теплоотдачи входит в определяемый критерий – критерий Нуссельта.
Критерий Нуссельта характеризует соотношение тепловых потоков, передаваемых за счет конвективного теплообмена и теплопроводности, и является искомой величиной
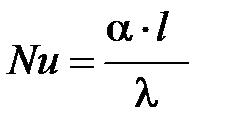. (105)
Критерий Рейнольдса характеризует соотношение между силами инерции и молекулярного трения (вязкости)
, (106)
Критерий Прандтля характеризует физические свойства жидкости и их влияние на конвективный теплообмен
. (107)
Критерий Грасгофа характеризует соотношение подъемной силы, возникшей вследствие разности плотностей неравномерно нагретых объемов жидкости и силы молекулярного трения, и является параметром интенсивности свободного движения жидкости
(109)
Критерий Пекле определяется следующим образом:
. (108)
Характеристики теплофизических свойств жидкостей, входящие в числа подобия, в общем случае зависят от температуры. Поэтому для определения численных значений критериев подобия указывается температура, при которой выбираются теплофизические характеристики жидкости.
|
|
|
Как было показано ранее, система дифференциальных уравнений, характеризующая процесс, приводится к безразмерному виду при соответствующих условиях однозначности. В конечном счете, получается общий вид критериального уравнения для нестационарного конвективного теплообмена
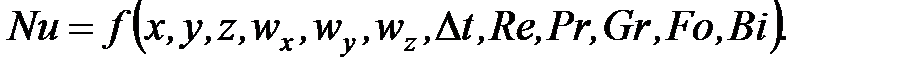(110)
Выражение для критериев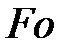 
и 
получены из дифференциальных уравнений теплообмена и теплопроводности (92) и (93).
Критерий Фурье (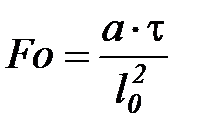 
) характеризует безразмерное время.
Написание критерия Био имеет форму записи аналогичную критерию Нуссельта
, (111)
где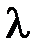 
– коэффициент теплопроводности твердого тела (в то время как в критерии Нуссельта 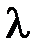- относится к окружающей среде); 
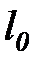– линейный размер твердого тела, м.
Для стационарного конвективного теплообмена уравнение (110) принимает вид
(112)
Уравнения вида (110, 112) называются критериальными.
В случае теплообмена, осложненного массообменном, критерий Нуссельта зависит еще от ряда критериев.
Следует отметить, что, поскольку критериальные уравнения получены на основе обработки экспериментальных данных, то в каждом случае указывается: диапазон применимости уравнения; определяющие температура и линейный размер.
Обработка и обобщение результатов эксперимента
Уравнение подобия конвективного теплообмена в условиях вынужденного движения жидкости имеет следующий вид
. (113)
На основе экспериментальных данных определяют необходимые величины и подсчитывают значения критериев подобия. Предположим, что зависимость между критериями подобия имеет степенной вид, т. е.
|
|
|
(113а)
где c, n, m – безразмерные постоянные величины.
Логарифмируя соотношение (113а) получаем
(114)
Наносим опытные значения критериев подобия во всем диапазоне проведенных исследований на график 
(рис. 7).
Очевидно, если связь (113) действительно является степенной, получим семейство прямых линий, каждая из которых соответствует определенному значению критерия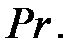 
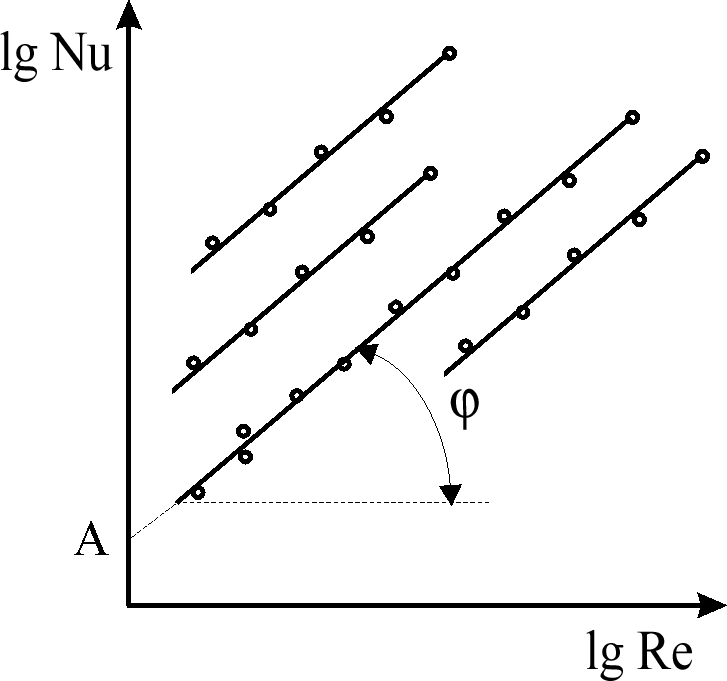
Рис. 7. Обобщение опытных данных в критериальной форме
В этом случае показатель степени при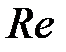 
определится как
, (115)
где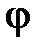 
– угол наклона прямых линий к оси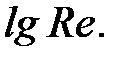 
Затем опытные данные наносят на график в координатах
(116)
Из этого графика определяют показатель степени m при критерии Pr
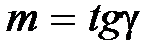, (117)
где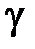 
– угол наклона прямой к оси 
.
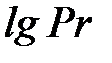Постоянная с определяется из соотношения
(118)
Таким образом, определяются все постоянные коэффициенты в критериальных уравнениях.
|
|
|
