 |
Дифференциальные уравнения конвективного теплообмена
|
|
|
|
Дифференциальное уравнение теплоотдачи получается при рассмотрении передачи теплоты теплопроводностью и конвективным теплообменом
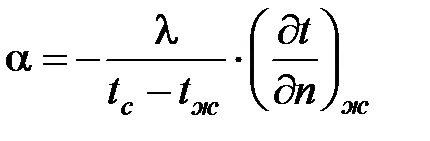(98)
Дифференциальное уравнение энергии при условии однородности и несжимаемости жидкости, отсутствия внутренних источников теплоты и работы расширения, а также постоянства физических параметров жидкости в пределах элементарного объема, формулируется следующим образом:
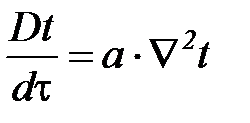, (99)
где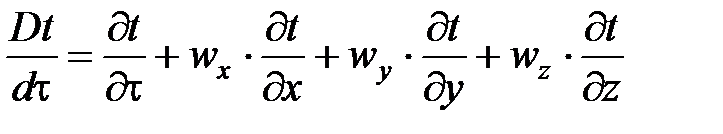 
– субстанциальная (полная) производная; 
– характеризует локальное изменение температуры во времени в какой-либо точке жидкости; 
– характеризует изменение температуры при переходе от точки к точке за счет конвективного теплообмена.
При 
, уравнение (99) переходит в уравнение теплопроводности для твердого тела без внутренних источников теплоты.
Дифференциальное уравнение неразрывности получается на основе закона сохранения массы, и для сжимаемой жидкости имеет следующий вид:
. (100)
Для несжимаемых жидкостей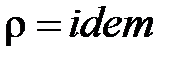 
уравнение (100) запишется в виде
. (101)
Уравнение движения (уравнение Навье-Стокса) в векторной форме можно представить в следующем виде
(102)
где 
– плотность;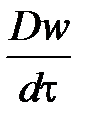 
– полная производная скорости; p – давление; g – ускорение свободного падения; 
– динамический коэффициент вязкости.
Полученная система дифференциальных уравнений описывает бесчисленное множество конкретных процессов.
Точные решения этой системы имеются только для отдельных частных случаев при ряде упрощающих предпосылок.
|
|
|
Основы теории подобия и метода анализа размерностей
В связи с ограниченными возможностями аналитического решения системы дифференциальных уравнений конвективного теплообмена, решающее значение приобретает эксперимент.
Цель экспериментального исследования заключается в получении на основе опытных данных эмпирических уравнений, по которым можно затем вести расчет теплообмена в подобных процессах.
Для этого необходимо сформулировать основные условия, при выполнении которых процессы будут подобны.
Эти условия формулируются в рамках теории подобия. Понятие подобия заимствовано из геометрии, где рассматриваются условия подобия геометрических фигур. Для подобия геометрических фигур достаточно соблюдения обычных признаков подобия (пропорциональность сходственных сторон, равенство углов идр. ). Для подобия физических процессов необходимо говорить о подобии физических величин и явлений. Два или несколько явлений будут подобны, если подобны все физические величины, характеризующие эти явления, т. е. подобные между собою явления имеют одинаковые безразмерные комплексы - критерии подобия. В связи с этим, в опытах нужно измерять те величины, которые входят в критерии подобия, характеризующие данный процесс.
Важной теоремой теории подобия является утверждение о том, что решение дифференциального уравнения, описывающего данный процесс, может быть представлено в виде функциональной зависимости между критериями подобия, характеризующими этот процесс и полученными из исходного уравнения и условий однозначности. Это утверждение говорит о том, опытные данные надо обработать в виде зависимости между критериями подобия.
Наряду с приведенными выше двумя теоремами подобия, важным является и утверждение о том, что подобны между собой те явления, которые принадлежат к одному классу, к одному роду и имеют равные определяющие критерии подобия. Этот вывод позволяет полученные в опыте расчетные зависимости распространить на группу явлений, подобных исследованному.
|
|
|
Таким образом, теория подобия, при наличии дифференциальных уравнений, описывающих рассматриваемый процесс, позволяет, не решая сами уравнения, получить выражения чисел (критериев) подобия и на их основе получить расчетные зависимости – уравнения подобия.
При отсутствии дифференциальных уравнений, описывающих изучаемый процесс, используется метод анализа размерностей.
Метод анализа размерностей базируется на π -теореме, которая устанавливает связь между функциями, выраженными через размерные и безразмерные параметры. Смысл π -теоремы заключается в том, что любая функциональная зависимость между m размерными величинами для измерения, которых использовано n основных единиц размерности, может быть представлена в виде N = m - n безразмерных комплексов, составленных из данных величин.
Применение метода анализа размерностей требует полного перечня основных величин, оказывающих существенное влияние на развитие рассматриваемого процесса.
Например, при вынужденной конвекции коэффициент теплоотдачи существенно зависит от следующих параметров:
(103)
где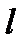 
– характерный для данного процесса линейный размер, м; w – скорость течения жидкости, м/с; ρ – плотность жидкости, кг/м3; ν = μ /ρ – кинематический коэффициент вязкости, м2/с; λ – коэффициент теплопроводности жидкости, Вт/(м·К); сp – удельная изобарная теплоемкость жидкости, Дж/(кг·K).
Непосредственное экспериментальное исследование этой зависимости, вследствие необходимости проведения большего числа опытов, практически неосуществимо.
Анализ размерностей в этом случае позволяет свести данное выражение (103) от семи размерных переменных к зависимости между тремя обобщенными безразмерными комплексами (к уравнению подобия).
|
|
|
