 |
Учет динамических нагрузок, действующих в приводе
|
|
|
|
В кинематических цепях коробок скоростей могут возникать динамические нагрузки, которые увеличивают статические нагрузки и, как правило, приводят к крутильным колебаниям валов привода.
Возникновение динамических нагрузок зависит от переходных процессов в период пуска и останова шпинделя и от периодически изменяющихся усилий резания в процессе обработки.
В станках с частыми пусками и остановами шпинделя необходимо учитывать инерционные воздействия, которые могут значительно превышать момент, приложенный в двигателе. Опреде-
ление динамических нагрузок в приводе является сложной задачей, так как на переходные процессы влияет целый ряд факторов (жесткость, силы трения, характеристика двигателя и др.). Привод в первом приближении можно рассматривать как упругую систему с массами на концах (рис. 63, а). Если приведенные моменты инерции двигателя и рабочего органа (шпинделя) станка обозна-

чить J1 и J2, момент двигателя M1 и момент сопротивления (от сил трения при пуске и торможении) М2, то можно получить общие дифференциальные уравнения движения для двигателя и рабочего органа станка, аналогичные уравнениям, рассмотренным выше [см. формулу (30), гл. 2].

Величина демпфирования зависит от рассеивания энергии колебаний в электродвигателе и в механической системе (в материале деталей, в стыках, в специальных демпфирующих элемен-
тах).
Решение уравнений (25) позволит определить характер движения и динамические нагрузки в приводе. Если не учитывать демпфирования в упругой системе привода, т. е. принять силы сопротивления, которые пропорциональны угловой скорости φ,равными нулю, получим
|
|
|
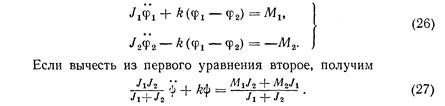
Решение этого общего уравнения производят в зависимости от начальных условий, которые назначают, исходя из условий пуска или торможения [4].
При пуске шпиндель станка за некоторый промежуток времени изменяет скорость движения от нуля до установившегося значения. Начальные условия при пуске (при t — 0) следующие: φ= 0 и φ = 0.
Характер движения при разгоне зависит также от момента M1 который зависит от механической характеристики двигателя, и от момента M 2, который определяется природой сил сопротивления (сил трения) в элементах привода.
Решение дифференциального уравнения (27) с учетом указанных начальных условий и при постоянных моментах М1 и М2
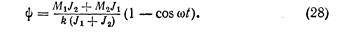
Возникающий в упругой системе момент
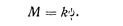
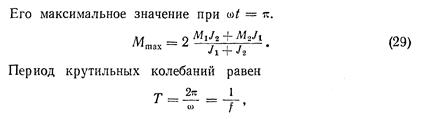
где f — частота собственных колебаний упругой системы [см.
формулу (38)].
Если считать, что момент инерции J2 значительно больше J1 что часто наблюдается в главном приводе тяжелых станков, то приняв J 1 — 0, получим
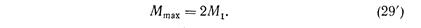
Таким образом, при переходных процессах (пуске, торможении, реверсе) динамические нагрузки в главном приводе могут достигать значительных величин [3] и их надо учитывать, особенно для станков с частыми включениями привода.
Решение дифференциального уравнения (25) с учетом затухания в системе привода при постоянных моментах Mt и М2 приводит к зависимости
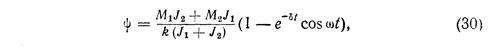
где Ь —параметр, характеризующий затухание (декремент затухания).
Соответственно углу закручивания изменяется и крутящий момент М = k * φ. График изменения крутящего момента в период mпуска с учетом затухания в системе показан на рис. 63, б.
Для станков с периодически изменяющимися усилиями резания, таких, как фрезерные, протяжные, строгальные и пр., динамические нагрузки на детали коробки скоростей действуют также
и в период обработки. Например, для фрезерных станков крутящий момент от сил резания, приложенный на шпинделе, является некоторой функцией времени Мкр = f(t). Эта функция опреде-
ляется характером фрезерования.
|
|
|
Если зубья фрезы врезаются в металл с нулевой толщиной стружки, то нарастание Мкр происходит постепенно. Если при врезании зуба сразу происходит снятие некоторой толщины ме-
талла, то происходит удар — мгновенный скачок Мкр. Практически возрастание Мкр происходит не мгновенно, а за некоторый промежуток времени. Если теоретически или экспериментально
установлен характер функции М (t), то на основании исследования возникающих крутильных колебаний можно установить значения крутящих моментов, учитывающих динамику процесса
резания.
Для этой цели следует составить дифференциальные уравнения, аналогичные уравнениям (25), где вместо момента сопротивления от сил трения будет момент сопротивления от сил резания как функция времени М (t). Эта функция времени является следствием тех сложных процессов пластического деформирования, которые происходят при резании и от которых зависит значение усилия резания Р. При этом следует иметь в виду, что взаимодействие инструмента с заготовкой является частью общей замкнутой динамической системы станка.
Для расчета динамических процессов в приводе в первом приближении следует исходить из простейших характеристик резания, которые учитывают основные факторы и позволяют указать
характер функции Р = f(t).
Зависимость усилия резания (а следовательно, и крутящего момента) от времени можно выразить соотношениями [36] и [46], которые вытекают из уравнений пластичности, упругости,
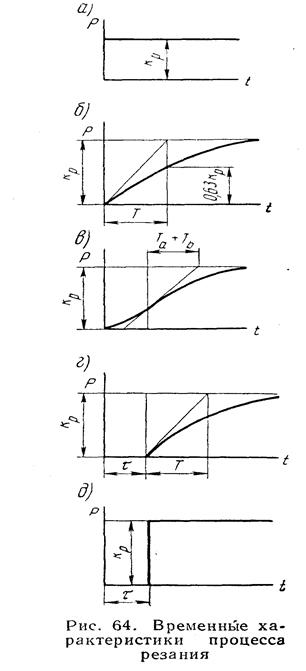
теплопередачи и механических свойств обрабатываемого материала (рис. 64):
1. При учете в этих уравнениях только членов, зависящих от сил упругости деформационной системы, получаем статическую характеристику сил резания, не зависящую от времени (рис.
64, а):
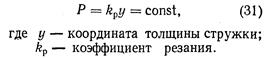
2. При учете одного из «вязких» сопротивлений в дополнение к упругому получаем зависимость (рис. 64, б)
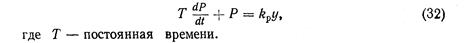
В этом случае временная характеристика сил резания имеет вид
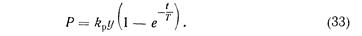
Такая зависимость силы (крутящего момента) от времени повышает общий порядок уравнений динамической системы станка на единицу.
3. При учете двух «вязких» сопротивлений, соединенных последовательно, или учете одного «инерционного» члена получаем
|
|
|
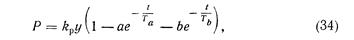
где постоянные, а, b, T а и T b можно выразить через постоянные времени Т1 и Т2, характеризующие два указанных сопротивления
(рис. 64, в).
4. При начальном медленном изменении усилия резания можно представить временную функцию, введя понятие запаздывания τ силы Р по отношению к у (рис. 64, г).
В этом случае уравнение для силы резания примет вид
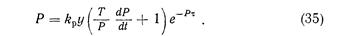
5. В упрощенном виде эту функцию (рис. 64, д) можно представить как

При более детальных расчетах необходимо учитывать динамическую характеристику резания, которая отражает особенности изменения силы резания во времени при изменении толщины среза и параметров процесса резания. Такие расчеты разработаны В. А. Кудиновым [36].
|
|
|


