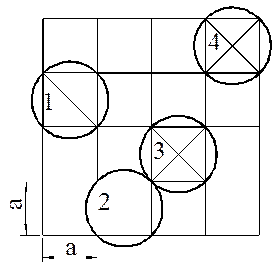Таблица 6 – Исходные данные к задачам 1, 2, 3, в мм

Таблица 6 – Исходные данные к задачам 1, 2, 3, в мм

Схема взаиморасположения геометрических тел	№ вар.	a	H	Геометрические тела
				Ц	К	П	С
				К	П	С	Ц
				П	С	Ц	К
				С	Ц	К	П
				С	П	К	Ц
				П	К	Ц	С
				К	Ц	С	П
				Ц	С	К	П
				П	К	С	Ц
				К	П	Ц	С
				Ц	К	П	С
				К	П	С	Ц
				П	С	Ц	К
				С	Ц	К	П
				С	П	К	Ц
				П	К	Ц	С
				К	Ц	С	П
				Ц	С	К	П
				П	К	С	Ц
				К	П	Ц	С
				Ц	К	П	С
				К	П	С	Ц
				П	С	Ц	К
				С	Ц	К	П
				С	П	К	Ц
				П	К	Ц	С
				С	П	К	Ц
				Ц	С	К	П
				П	К	С	Ц
				К	П	Ц	С

 

той плоскости проекций, на которой строится изображение.

После нанесения преподавателем на поверхностях проекций линий, студенты достраивают недостающие проекции этих линий самостоятельно (с учетом их видимости). Невидимые участки линий наносятся штриховой линией.

Для определения видимых и невидимых участков линий используют границу видимости, определяемую точками, лежащими на очерках поверхности.

Основные положения:

– точка лежит на поверхности, если она лежит на линии, принадлежащей этой поверхности;

– линия лежит на поверхности, если все ее точки принадлежат поверхности.

Наглядное (аксонометрическое) изображение группы геометрических тел строится в прямоугольной изометрии согласно ГОСТ 2. 317-69.

Прямоугольная изометрия получается в случае, если все три оси декартовой системы координат, при проецировании на аксонометрическую плоскость проекций располагаются под равными углами к этой плоскости, а приведенные коэффициенты равны между собой (k_x=k_y=k_z). Угол между аксонометрическими осями в прямоугольной изометрии составляет 120⁰.

В прямоугольной диметрии коэффициент искажения k_y в два раза меньше чем k_x и k_z. Ось O¢ Z¢ располагают вертикально, тогда оси O¢ X¢ и O'Y¢ образуют с линией горизонта соответственно углы 7⁰  10¢ и 41⁰ 25¢.

Аксонометрический чертеж обладает всеми свойствами параллельного проецирования. Аксонометрическая проекция квадрата – ромб, а окружности – эллипс. Построить аксонометрическое изображение объекта можно, либо построением каждой из характерных точек объекта по их координатным ломанным, либо с помощью вторичных проекций.

В прямоугольной изометрии изображают объекты криволинейной формы. В прямоугольной диметрии изображают объекты призматической и пирамидальной формы. В косоугольной фронтальной диметрии изображают детали, имеющие ряд окружностей, расположенных во взаимно параллельных плоскостях.

К преимуществам аксонометрического чертежа относятся: однопроекционность (наличие одной проекции), наглядность (возможность установить по чертежу форму объекта по его изображению), обратимость (возможность реконструкции объекта по его изображению), а к недостаткам – сложность построений изображений и измеримости объекта.

 

 

Рисунок 4

2. 4. Моделирование сечений геометрических тел

Цель задания – закрепление знаний студентов по построению плоских сечений геометрических тел.

Содержание работы. Задание включает две задачи.

Задача 1. Построить три проекции усеченной пирамиды.

Задача 2. Построить три проекции усеченной сферы.

Рекомендации к выполнению задания. Данные для выполнения задания взять из таблиц 7 и 8 по варианту. Задачи выполнить на одном листе формата А3(420х297). Три проекции пирамиды выполнить на левой половине листа, а три проекции сферы – на правой. Образец выполнения задания приведен на рисунке 5.

Сечение – это плоская фигура, ограниченная линией пересечения плоскости с поверхностью. Сечение пирамиды – это плоский многоугольник, число вершин которого равно числу пересеченных плоскостью ребер. Сечение сферы – окружность.

Сечение геометрических тел плоскостями строится в следующей последовательности:

– определить расположение поверхности и секущих плоскостей относительно друг друга и плоскостей проекций;

– определить количество секущих плоскостей;

– построить проекции опорных и промежуточных точек линии контура сечения на каждом участке;

– определить проекции линии контура сечения, соединения соответствующие опорные и промежуточные точки;

К опорным точкам относятся: экстремальные точки (высшая и низшая, самая близкая и самая удаленная, крайняя левая и крайняя правая) и точки видимости (точки, разграничивающие линию сечения на видимую и невидимую части). Видимыми будут проекции тех точек линии контура сечения, которые принадлежат видимым на этой проекции граням, ребрам или образующим поверхности.

Основные положения:

– если плоскость проецирующаяся, то одна проекция контура сечения многогранника прямая, а другая – многоугольник;

– если плоскость проецирующаяся, то одна проекция сечения сферы - прямая линия, а другая – окружность или эллипс.

 

 

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: