 |
Интегрирование тригонометрических функций
|
|
|
|
Рассмотрим интегралы вида 
. Такие интегралы могут быть сведены к интегралам от рациональных функций заменой переменной 
, где 
Такая замена называется универсальной тригонометрическая подстановкой.
В этом случае,
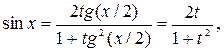
Тогда
.
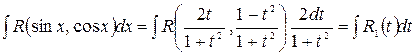Пример 7. Найти 
Решение:
Положим 
. Тогда, используя выражения через t для dx и sin x, указанные выше, получаем, что искомый интеграл равен
При вычислении интегралов вида
рассмотрим частные случаи:
n – нечётное
n, m – чётные, 
.
применяют формулы тригонометрии:
При вычислении интегралов вида 
делают замену 
, тогда
Если интеграл имеет вид
,
где n, m – чётные, применяют формулу:
Пример 8. Вычислить интегралы:
а) 
б) 
Решение:
а) 
б) 
При вычислении
используют формулы
Интегрирование иррациональных выражений
При вычислении интегралов, содержащих иррациональные выражения применяют замену переменной.
Если 
,
то 
, где 
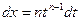
Если 
то 
, где 
Лекция13
Определённый интеграл, его свойства
Пусть на отрезке 
задана функция y=f(x). Разобьем отрезок на n элементарных отрезков точками 
. На каждом отрезке 
разбиения выберем некоторую точку 
и положим 
, где 
. Сумму вида
будем называть интегральной суммой для функции y=f(x) на . Очевидно, что интегральная сумма зависит как от способа разбиения отрезка точками 
, так и от выбора точек 
на каждом из отрезков разбиения , .
 |
Если существует предел 
, не зависящий от способа разбиения отрезка и выбора точек 
, то этот предел будем называть определённым интегралом функции f(x) на отрезке и обозначать символом 
т.е.
Функция f(x) в этом случае называется интегрируемой на отрезке . При этом f(x) называется подынтегральной функцией, f(x)dx – подынтегральным выражением, а числа a и b – пределами интегрирования (a – нижний предел, b – верхний предел), а сумма 
– интегральной суммой.
|
|
|
Теорема. Если функция f(x) непрерывна на отрезке , то она интегрируема на этом отрезке.
Свойства определённого интеграла
1. 
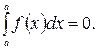
2. Постоянный множитель можно выносить за знак определённого интеграла:
3. Определённый интеграл от суммы двух функций равен сумме определённых интегралов от этих функций:
4. При перестановке пределов интегрирования определённый интеграл меняет знак на противоположный:
5. Интеграл по отрезку равен сумме интегралов по его частям:
где a<c<b.
6. Теорема об оценке интеграла
Если 
для 
, тогда значения интеграла от этой функции не менее произведения m на длину отрезка и не более произведения M на длину отрезка.
7. Теорема о среднем значении
Если f(x) непрерывна на отрезке , то существует такое значение 
, что f(x0)=fср – среднее значение f на отрезке.
Теорема Ньютона-Лейбница
Если функция f(x) непрерывна на отрезке и F(x) – первообразная функции f(x) на этом отрезке, то
Эта формула называется формулой Ньютона-Лейбница.
При вычислении интегралов ее часто записывают в виде
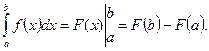
Например, 
= 
Замена переменной в определённом интеграле
Предположим, что функция f(x) непрерывна на отрезке , функция 
имеет на отрезке 
непрерывную производную, при этом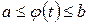 
и 
Тогда
Пример 9. Найдём 
Решение:
Воспользуемся подстановкой x= sin t; тогда 
. Найдём новые пределы интегрирования: если х=0, то t=0, если х=1, то 
. Получим
.
Интегрирование по частям
Пусть u=u(x), v=v(x) – непрерывно дифференцируемые на функции. Тогда справедлива формула
или
Пример 10. Найти 
Решение: Положим u=x,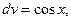 
откуда 
Согласно формуле находим
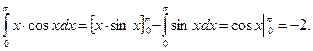
Геометрические приложения определённого интеграла
|
|
|
