 |
Простейшие типы дифференциальных уравнений первого порядка.
|
|
|
|
1) Уравнение с разделёнными переменными
или
.
Решая первое уравнение, получим 
.
Интегрируя, найдём общее решение 
.
Решая второе, получим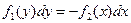 
.
Интегрируя, найдём общее решение.
2) Уравнение с разделяющимися переменными,
или
.
Разделим обе части первого уравнения 
на 
и умножим на 
, получим уравнение с разделёнными переменными
Для второго уравнения: разделим обе части на произведение 
, получим также уравнение с разделёнными переменными
.
Операция деления уравнения на произведение 
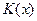называется разделением переменных.
При делении на произведение можно потерять некоторые решения, которые получаются из уравнения
.
Определяя из этого уравнения решения 
, следует проверить, является ли оно решением исходного уравнения. Если не является, его следует отбросить, а если является, то проверить, входит ли оно в общий интеграл. Если входит, то оно есть частное решение, а если не входит, то это решение называется особым.
Пример 17 Решить уравнение 
.
Решение:
Разделим уравнение на произведение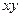 
, получим:
.
Интегрируя, получим общий интеграл:
.
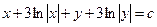
В этом уравнении имеет вид 
. Его решение 
, 
является решением исходного уравнения, но не входит в общий интеграл. Следовательно, решение , является особым.
Пример 18 Найти общее решение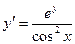 
.
Решение:
;
;
интегрируя, найдем общее решение
или 
;
;
;
3) Однородные уравнения.
Функция 
называется однородной степени 
, если для любых 
и 
выполняется равенство
Если функции 
и 
однородные одной и той же степени , то дифференциальное уравнение 
называется однородным.
Однородное уравнение всегда можно привести к виду
,
решается подстановкой:
или 
; 
.
Пример 19 Решить 
.
|
|
|
Решение:
Данное уравнение является однородным, т.е. функции 
, 
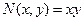однородные степени 
. Сделаем замену Тогда уравнение перепишется так:
;
;
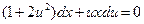разделяя переменные, получим:
;
;
;
Так как у нас 
, то 
, 
, 
.
Лекция15
Линейные дифференциальные уравнения
Уравнение 
,
где 
, 
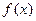- непрерывная функция от 
на интервале 
, называется линейным дифференциальным уравнением первого порядка.
Неизвестная функция 
и её производная входят в это уравнение в первой степени – линейно.
Линейные уравнения обычно решают методом Бернулли.
Представим искомую функцию в виде произведения двух неизвестных функций 
и 
.
Пусть 
, тогда 
или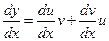 
,
и уравнение примет вид
или 
.
Полученное уравнение разобьём на два таким образом:
1) Выберем функцию так, чтобы сумма второго и третьего слагаемых обратилась в нуль:
;
2) 
.
Решаем первое: так как 
, относительно имеем уравнение 
с разделяющимися переменными:
или 
Функцию 
подставим во второе уравнение:
, откуда 
.
.
Найдём общее решение по формуле
,
подставив найденные функции вместо 
, .
Пример 20 Решить уравнение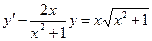 
.
Решение:
Положим , .
Подставляя выражения для 
и 
в данное уравнение получим:
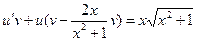
1) 
2) 
.
Решаем первое уравнение:
После разделения переменных получим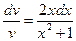 
. Отсюда 
или 
.
Решаем второе уравнение:
Подставим найденное значение , получим:
.
Отсюда, разделяя переменные и интегрируя, находим функцию :
.
Теперь можно записать общее решение данного дифференциального уравнения:
или
.
Уравнением Бернулли
называется уравнение вида
,
где 
– любое вещественное число.
Если равно нулю или единице, то мы получим линейное дифференциальное уравнение.
Уравнение Бернулли можно сразу решать методом Бернулли, полагая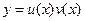 
. Следует отметить, что при 
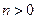функция 
является решением Бернулли.
Пример 21 Решить уравнение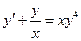 
.
Решение:
Приведём решение методом Бернулли.
Полагая
;
|
|
|
;
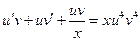получим
1) 
; 
; 
; 
.
2) Подставим найденную функцию :
; 
; 
; 
; 
; 
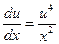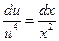и окончательно 
.
Лекция16
|
|
|
