 |
Предельный признак сравнения
|
|
|
|
Если существует предел (в предположении, что 
)
то оба ряда сходятся или оба расходятся одновременно.
Примеры 37 Исследовать сходимость ряда
Решение:
Члены ряда не превосходят соответствующих членов сходящегося ряда, составленного из членов геометрической прогрессии с общим членом
:
Согласно признаку сравнения, данный ряд также сходится.
Примеры 38 Исследовать сходимость ряда
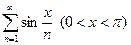
Решение:
Ряд расходится по предельному признаку сравнения, так как
,
где известно, что гармонический ряд
.
Лекция19
Знакопеременные ряды. Признак Лейбница
Знакопеременным рядом называется ряд, членами которого являются действительные числа произвольного знака.
Например,
1) 
2) 
3) 
Знакопеременный ряд называется знакочередующимся, если соседние его члены имеют различные знаки.
Например, 
.
Знакопеременный ряд 
называется:
· Абсолютно сходящимся, если сходится ряд составленный из модулей его членов 
.
· Условно сходящимся, если он сходится, но не сходится абсолютно.
Имеют место следующие свойства абсолютно сходящихся рядов:
1)Всякий абсолютно сходящийся ряд сходится.
2)Если в абсолютно сходящемся ряде произвольным образом переставить члены, то полученный ряд также будет абсолютно сходится, а сумма его будет равна сумме исходного ряда.
Пример 37 Исследовать ряд 
на сходимость.
Решение:
Составим ряд из модулей 
, он сходится.
По признаку сравнения, так как
Ряд 
– сходится, следовательно сходится и ряд .
Таким образом сходится абсолютно ряд .
Для знакочередующихся рядов имеет место
Признак сходимости Лейбница.
Если члены знакочередующегося ряда
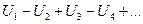
1) монотонно убывают по абсолютной величине, т. е.
|
|
|
,
и
2) общий член ряда стремится к нулю, 
,
то:
1) ряд сходится;
2) его сумма не превосходит величины первого члена ряда
;
3) модуль суммы остатка ряда не превосходит абсолютной величины первого отброшенного члена (первого члена остатка):
и имеет знак своего первого члена.
Пример 38 Исследовать на сходимость ряды
а) 
б) 
Решение:
а) ряд сходится по признаку Лейбница, так как члены ряда монотонно убывают по абсолютной величине
и общий член ряда стремится к нулю, 
,
б) ряд сходится по признаку Лейбница:
; 
.
Если положить его сумму S, приближенно равной сумме первых шести членов этого ряда, то получим ошибку, абсолютная величина которой меньше, чем
S=0,907.
Функциональные ряды. Степенные ряды
Функциональным рядом называется выражение
,
члены которого 
являются функциями от 
.
Придавая числовое значение 
, мы получаем числовой ряд
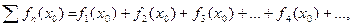
который может быть как сходящимся, так и расходящимся.
Множество тех значений, , при которых функциональный ряд сходится, называется его областью сходимости. Ясно, что в области сходимости сумма функционального ряда является некоторой функцией от . Обозначим се через 
.
Функциональный ряд сходится в точке x0, если сходится числовой ряд.
Функциональный ряд сходится на интервале J, если он сходится в каждой точке этого интервала.
На интервале сходимости J сумма ряда есть некоторая функция S(x).
Например, используя известные признаки сходимости числовых рядов, можно найти интервалы сходимости функциональных рядов:
1) 
.
2) 
; 
сходится для 
3) 
– ряд Дирихле: при 
сходится, при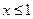 
расходится.
4) 
расходится для .
Специальный класс функциональных рядов составляют гак называемые степенные ряды вида
= 
,
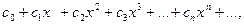где 
-- последовательность действительных чисел, называют коэффициентами ряда.
Выясним, какой вид имеет "область сходимости" степенного ряда, тоесть множество 
тех значений переменной, для которых ряд сходятся.
|
|
|
Теорема Абеля.
Если степенной ряд сходится в точке 
, то он сходится и притом абсолютно в интервале 
, то есть при всех значениях , удовлетворяющих условию. 
.
Следствие:
Если степенной ряд расходится при некотором значении 
, то он расходится и при всех значениях 
.
Любой степенной ряд сходится при значении 
. Естьстепенныеряды, которые сходятся только при и расходятся приостальныхзначениях .
Область сходимости может состоять из всех точекоси Ох, другимисловами, ряд может сходится при всех .
Пример 39 Исследовать сходимость ряда 
.
Решение:
Ряд 
представляет геометрическую прогрессию со знаменателем , сходится при 
и расходитсяпри 
.
Из теоремы Абеля и ее следствия получаем, что все точки сходимости расположены от начала координат не дальше, чем любая из точек расходимости. Совершенно ясно, что точки сходимости будут целиком заполнять некоторый интервал с центром в начале координат.
Таким образом, можно сказать, что для каждого степенного ряда, имеющего как точки сходимости, так и точки расходимости, существует такое положительное число 
, что для всех , по модулю меньших 
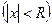, ряд абсолютно сходится, а для всех , по модулю больших 
, ряд расходится.
Что касается значений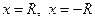 
здесь могут быть различные возможности: ряд может сходится в обеих точках, или только в одной из них, или ни в одной. При этом ряд может сходиться как абсолютно, так и условно.
Радиусом сходимости степенного ряда называетсятакое число , что для всех , 
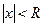, степенной ряд сходится, а для всех 
, расходится. Интервал 
называется интервалом сходимости.
Условимся для рядов, расходящихся при всех , кроме . считать 
, а для рядов, сходящихся при всех , считать 
.
Как найти радиус сходимости?
Если все коэффициенты степенного ряда, начиная с некоторого, отличны от нуля, то его радиус сходимости равен пределу при 
отношения абсолютных величин коэффициентов общего и следующего за ним членов ряда.
Составим ряд из абсолютных величин членов ряда
Найдем отношение 
для этого ряда:
а затем предел его при :
Здесь множитель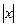 
вынесен за знак предела, как не зависящий от 
и введено обозначение
,
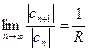если этот предел существует и не равен нулю. Согласно признаку Даламбера, ряд сходится, если 
,. откуда 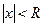. Отсюда следует, что ряд сходится, и притом абсолютно, при значениях .
|
|
|
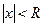Согласно томуже признаку Даламбера, ряд расходится, если 
или . Однако в этом случае из признака Даламбера следует, что члены ряда не стремятся к нулю. Тогда при не стремятся к нулю и члены ряда, а потому и он расходится при значениях . Следовательно, согласно определению, число – радиус сходимости степенного ряда. из соотношения получим
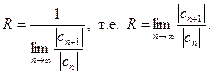
Пример 40 Найти радиус сходимости ряда 
Решение:
Пример 41 Найти область сходимости степенного ряда
Решение:
Найдем отношение
т. е. ряд сходится только при и расходится при остальных значениях .
Пример 42 Найти область сходимости степенного ряда:
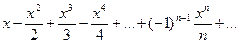
Решение:
Здесь 
Исследуем сходимость ряда на концах интервала сходимости.
При 
имеем ряд 
он сходится по теореме Лейбница.
При 
имеем ряд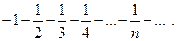 
, который расходится как произведение расходящегося гармонического ряда на -1. Следовательно; областью сходимости служит полуинтервал 
.
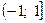Пример 43 Найти область сходимости степенного ряда
Решение:
Найдем радиус сходимости ряда
Исследуем сходимость ряда при значениях 
. Подставив их в данный ряд соответственно получим 
Оба ряда расходятся, так как не выполняется необходимое условие сходимости (их общие члены не стремятся к нулю при ). На обоих концах интервала сходимости данный ряд расходится а область его сходимости 
Замечание.
Формула радиуса сходимости степенного ряда получена в предположении, что все коэффициенты членов ряда начиная с некоторого, отличны от нуля. Применение формулы допустимо только в этих случаях. Если это условие нарушается, то радиус сходимости степенного ряда следует искать или с помощью признаков Даламбера. Коши, или же сделав замену переменной, преобразованием ряда к виду в котором указанное условие выполняется.
|
|
|
