 |
Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и специальной правой частью
|
|
|
|
Рассмотрим уравнение второго порядка
,
где коэффициенты 
– числа, 
.
Согласно теореме о структуре общего решения, оно имеет вид:
,
где 
– общее решение однородного дифференциального уравнения,
– частное решение неоднородного дифференциального уравнения.
Вид функции устанавливается по виду правой части дифференциального уравнения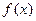 
.
Сначала, как и при методе Лагранжа, находится общее решение однородного дифференциального уравнения
,
его характеристическое уравнение имеет вид
,
где 
– его корни.
Затем отыскивается частное решение неоднородного уравнения Рассмотрим некоторые частные случаи:
1) пусть правая часть уравнения имеет вид
,
тогда частное решение определяется следующим образом:
, если 
,
, если 
,
, если 
,
где А – неопределенный коэффициент, находится методом неопределенных коэффициентов (см. пример).
2) пусть правая часть имеет вид
где 
– многочлен степени 
, тогда частное решение определяется следующим образом:
, если ,
, если ,
, если ,
где А,B,C…D – неопределенные коэффициенты, находятся методом неопределенных коэффициентов (см. пример).
В частности, если правая часть имеет вид
где – многочлен степени , тогда частное решение определяется следующим образом:
, если 
,
, если 
,
, если 
.
3) пусть правая часть имеет вид
или
,
тогда частное решение определяется следующим образом:
, если 
,
, если 
.
В частности, если правая часть имеет вид
или 
,
тогда частное решение определяется следующим образом:
, если 
,
, если 
.
4) пусть правая часть имеет вид
,
тогда частное решение определяется следующим образом:
,
где 
; если
Пример 28 Записать вид частного решения следующих дифференциальных уравнений:
|
|
|
а) 
; б) 
;
в) 
; г) 
.
Решение:
а) .
Решаем соответствующее однородное уравнение 
.
Составляем характеристическое уравнение: 
, находим корни: 
; 
; 
.
Общее решение однородного уравнения 
.
Правая часть исходного уравнения имеет вид: 
; 
; 
.
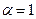Т.к. число 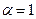не является корнем характеристического уравнения, а 
– многочлен первой степени, то частное решение уравнения имеет вид:
.
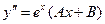г) .
Решаем соответствующее однородное уравнение 
, находим корни 
.
Общее решение однородного уравнения: 
.
Правая часть исходного уравнения имеет вид: 
, отсюда 
, 
.
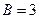Т.к. число 
не является корнем характеристического уравнения, а 
и 
– многочлены нулевой степени, то частное решение уравнения имеет следующий вид:
.
Выполнить примеры б, в самостоятельно.
Пример 29 Решить следующие дифференциальные уравнения:
а) 
; б)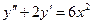 
;
в) 
.
Решение:
а) Решаем соответствующее однородное уравнение:
.
Составляем характеристическое уравнение 
, находим корни ; 
.
Общее решение однородного уравнения 
.
По виду правой части 
, находим частное решение
,
число 
.
Методом неопределённых коэффициентов найдём 
.
; 
.
Подставим в исходное уравнение: 
.
Получим
,
тогда частное решение 
.
Общее решение исходного дифференциального уравнения
б) ;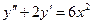 
; 
.
Данная задача является задачей Коши, требуется найти частное решение, удовлетворяющее исходному уравнению и поставленным начальным условиям.
Решаем соответствующее однородное уравнение:
.
Составляем характеристическое уравнение ,
находим корни ; .
Общее решение однородного уравнения 
.
По виду правой части – многочлену второй степени 
, находим частное решение.
Число 
является корнем характеристического уравнения, а – многочлен второй степени, тогда частное решение имеет вид:
.
Методом неопределённых коэффициентов найдём , 
, 
.
Так как
;
,
то подставляя в исходное уравнение, получим
|
|
|
.
После приведения подобных: 
.
Приравняв коэффициенты при одинаковых степенях 
у многочленов, стоящих в левой и правой части равенства, получим систему:
решая ее, найдем
Отсюда частное решение 
.
Общее решение 
.
Найдём частное решение, удовлетворяющее начальным условиям.
В общее решение подставим 
.
Чтобы удовлетворить второму условию 
, найдём
.
Положим 
, 
. Получим 
.
Получим систему: 
Частное решение 
.
в) .
Решаем соответствующее однородное уравнение 
.
Его характеристическое уравнение 
.
Правая часть исходного уравнения имеет вид:
,
следовательно, ; 
.
не является корнем характеристического уравнения. Многочлены 
– многочлены нулевой степени, поэтому частное решение ищем в виде:
.
Методом неопределённых коэффициентов найдём и .
;
.
Подставим в исходное уравнение:
;
.
Приравниваем коэффициенты при одинаковых тригонометрических функциях:
; 
;
; 
.
Найдено частное решение 
.
Общее решение 
.
Пример 30 Решить уравнение 
Решение:
Общее решение однородного уравнения будет
Частное решите неоднородного уравнения будем искать в виде суммы двух частных решений, так как правая часть есть сумма функций 
:
Подставляя в исходное уравнение получим:
Приравнивая коэффициенты при подобных членов в обеих частях уравнения получим:
итак, общее решение имеет вид
Лекция18
РЯДЫ
Числовые ряды. Основные понятия. Необходимый признак сходимости ряда
Основные понятия
Пусть задана некоторая бесконечная последовательность чисел:
выражение
называется бесконечным числовым рядом (или просто рядом).
Числа – называются членами ряда, а член ряда 
– его общим членом.
Примеры рядов:
1) 
2) 
3) 
Ряд можно задать с помощью общего члена, например, 
определяет следующий ряд:
Частичной суммой 
числового ряда называетсясуммаего первых n членов,
Суммой числового ряда S называется предел последовательности его частичных сумм, если этот предел существует
,
причем ряд называется сходящимся, в противном случае, если же 
не существует, или 
то ряд называется расходящимся.
Пример 31 Исследовать на сходимость ряды
а) 
б) 
Решение:
|
|
|
а) Рассмотрим ряд . Найдем его частичные суммы 
Последовательность его частичных сумм 1,0,1,0.1,0... не имеет предела, следовательно ряд расходится.
б) Рассмотрим ряд
найдем его частичные суммы:
Так как 
то рассматриваемый ряд сходится: его сумма равна 1.
Пример 32 Исследовать на сходимость
Решение:
Данный ряд составлен из членов геометрической прогрессии с первым членом 
и знаменателем 
(будем считать 
):
,
известно, что сумма первых n членов геометрической прогрессии определяется по формуле
Найдем 
, очевидно, что при 
, ряд сходится и его сумма 
. В остальных случаях, при 
, ряд расходится (доказать самостоятельно).
Например, ряд 
сходится, т.к. q= 
и его сумма 
, а ряд 
расходится, т.к. q= 
.
|
|
|
