 |
Линейная модель вероятности
|
|
|
|
Воспользуемся обычной линейной моделью регрессии: У = ХT  +
+  . Т. к. У может принимать только два значения 0 или 1 и М (
. Т. к. У может принимать только два значения 0 или 1 и М ( ) = 0 (М – знак математического ожидания), то
) = 0 (М – знак математического ожидания), то
М (У) = 1  Р (У = 1)+0
Р (У = 1)+0  Р (У = 0) = Р (У = 1) = ХT
Р (У = 0) = Р (У = 1) = ХT  .
.
Таким образом, исходная модель может быть записана в виде
Р (У = 1) = ХT  ,
,
поэтому её называют линейной моделью вероятностей.
В отличие от обычной линейной регрессионной модели эта модель обладает рядом особенностей. Во-первых, ошибка  может принимать только два значения –
может принимать только два значения –  ХT
ХT  с вероятностью Р (У=1) и
с вероятностью Р (У=1) и  =
=  ХT
ХT  с вероятностью 1
с вероятностью 1  Р (У=1). Это не позволяет считать, что ошибка распределена по нормальному закону. К тому же дисперсия ошибки равна D(
Р (У=1). Это не позволяет считать, что ошибка распределена по нормальному закону. К тому же дисперсия ошибки равна D( ) = ХT
) = ХT  ХT
ХT  ), т. е. зависит от регрессоров, а значит, имеем модель с гетероскедастичными остатками. Кроме того, прогнозные значения зависимой переменной могут не лежать внутри отрезка [0,1], что значительно снижает ценность такой модели для практических расчётов. Обычно такую модель используют для первичной обработки данных для сравнения с результатами более сложных моделей.
), т. е. зависит от регрессоров, а значит, имеем модель с гетероскедастичными остатками. Кроме того, прогнозные значения зависимой переменной могут не лежать внутри отрезка [0,1], что значительно снижает ценность такой модели для практических расчётов. Обычно такую модель используют для первичной обработки данных для сравнения с результатами более сложных моделей.
P robit- и Logit- модели
В линейной модели вероятностей вероятность события является линейной функцией независимых переменных, что является её основным недостатком. Этот недостаток можно преодолеть, записав вероятность как функцию, область значений которой лежит в интервале [0,1]. Известно, что таким свойством обладают функции стандартного нормального и логистического распределений:
F(u) = Ф(u) =  и F(u) =
и F(u) =  =
=  , где u = ХT
, где u = ХT  .
.
Соответственно такие модели называются p robit- и logit- моделями.
Вопрос о том, какую модель предпочесть, решается исследователем, тем более что для достаточно близких по модулю к нулю значений u обе функции дают примерно одинаковые результаты. Логистическая функция более проста в вычислительном аспекте, поэтому используется чаще.
|
|
|
Рассмотрим более подробно эту модель. Пусть р = Р(А) – вероятность некоторого события. Отношение 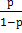 называют шансами этого события. Например, если р = 1/3, то р/(1
называют шансами этого события. Например, если р = 1/3, то р/(1  р) = ½, и шансы на то, что событие А произойдёт, равны ½ (или в два раза ниже). Логарифм отношения р/(1
р) = ½, и шансы на то, что событие А произойдёт, равны ½ (или в два раза ниже). Логарифм отношения р/(1  р) называют логитом, logit(p) = ln(p/1
р) называют логитом, logit(p) = ln(p/1  p). Если р
p). Если р  , то больше щансов, что событие А произойдёт. Пусть теперь р = Р(у=1). В логит
, то больше щансов, что событие А произойдёт. Пусть теперь р = Р(у=1). В логит  модели р =
модели р = 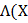 Т
Т  ) = exp((
) = exp(( Т
Т  )/(1+
)/(1+  Т
Т  )), 1
)), 1  р = 1/(1+
р = 1/(1+  Т
Т  ), так что logit(p) =
), так что logit(p) =  Т
Т  , т. е. логит
, т. е. логит  модель линейна в отношении логита. Отсюда и б о льшая простота этой модели в вычислительном аспекте.
модель линейна в отношении логита. Отсюда и б о льшая простота этой модели в вычислительном аспекте.
Поскольку эти модели не линейны по параметрам, то для оценивания их параметров используется метод максимального правдоподобия, который здесь не обсуждается. Вычисления по этому методу следует предоставить вашему компьютерному пакету.
Оценка качества подгонки данных моделью в этом случае отличается от аналогичной в линейном МНК. Вместо коэффициента множественной детерминации вычисляется псевдо R2 = 1 
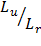 , где
, где 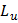 и
и  – соответственно значения функции правдоподобия, когда не все коэффициенты регрессии равны нулю и когда все коэффициенты регрессии равны нулю. В EViews эта статистика называется McFadden R-squared.
– соответственно значения функции правдоподобия, когда не все коэффициенты регрессии равны нулю и когда все коэффициенты регрессии равны нулю. В EViews эта статистика называется McFadden R-squared.
Известно, что значения этого показателя находится в интервале [0,1] и чем ближе его значение к единице, тем точнее уравнение. Здесь речь идёт о качестве подгонки наблюдаемых частот зависимой переменной расчётными вероятностями или насколько точно модель предсказывает наблюдаемые частоты.
Ещё один тест на точность модели, выдаваемый пакетом EViews, называется LR-тестом и рассчитывается из соотношения LR =  2(
2( )
)  ln(
ln(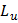 )). Здесь тестируется гипотеза о том, что все коэффициенты модели равны нулю. Если эта гипотеза верна, то LR-статистика следует хи-
)). Здесь тестируется гипотеза о том, что все коэффициенты модели равны нулю. Если эта гипотеза верна, то LR-статистика следует хи-  распределению с m степенями свободы.
распределению с m степенями свободы.
Пример 5. Модель бинарного выбора
|
|
|
Рассмотрим пример моделирования наличия компьютера у индивидуума в зависимости от его социального статуса (Ben Vogelvang, 2005).
Переменная отклика (зависимая переменная) PC равна нулю, если индивид не имеет компьютера, и равна единице, если компьютер есть. Зависимые переменные: EDUC – образование (сколько лет учился), INC – доход (от менее 10 000 до более 50 000 с интервалом в 10 000, т. е. принимает значения, равные 0,1,2,3,4,5) и AGE – возраст (18  81 год). Было опрошено 59 человек.
81 год). Было опрошено 59 человек.
Линейная модель вероятностей показана на рисунке 2.25. Поскольку образование имеет малое влияние на факт наличия компьютера, попробуем скорректировать оценки ошибок по форме Уайта (рисунок 2.26). Как видим, незначимость образования осталась, хотя расчётный уровень значимости уменьшился. Получили, что изменение показателя наличия компьютера описывается изменением этих трёх признаков на 44%.
Из графика (рисунок 2.27) видно, что некоторые расчётные значения переменной отклика линейной модели вероятностей вышли из интервала [0,1] (есть и больше единицы и отрицательные значения), что «говорит» о недостатках этой модели.

Рисунок 2.25 – Исходная линейная модель вероятностей

Рисунок 2.26 – Линейная модель вероятностей со стандартными ошибками в
форме Уайта

Рисунок 2.27 – График фактических, расчётных значений и остатков линейной модели вероятностей
Рассмотрим этот же пример для logit- модели. Для этого в окне спецификации модели (заставка «Specificftion») в позиции «Method» выбираем «BINARY» – модели бинарного выбора и в позиции «Binary estimation method» ставим точку «Logit» (рисунок 2.28). Тем самым заказали оценку параметров logit- модели.

Рисунок 2.28 – Выбор метода оценивания модели бинарного выбора
После оценки получили рисунок 2.29. Псевдо R-квадрат модели равен 0,58, что «говорит», что точность предсказания удовлетворительная, а LR-статистика имеет расчётный уровень значимости меньше 0,05, что говорит о том, что уравнение регрессии значимо. Кроме того, в отчёте указано, что в выборке представлены 28 человек, не имеющих компьютера и 31 – имеющий компьютер, общее число наблюдений – 59 (см. нижнюю часть рисунка 2.29).
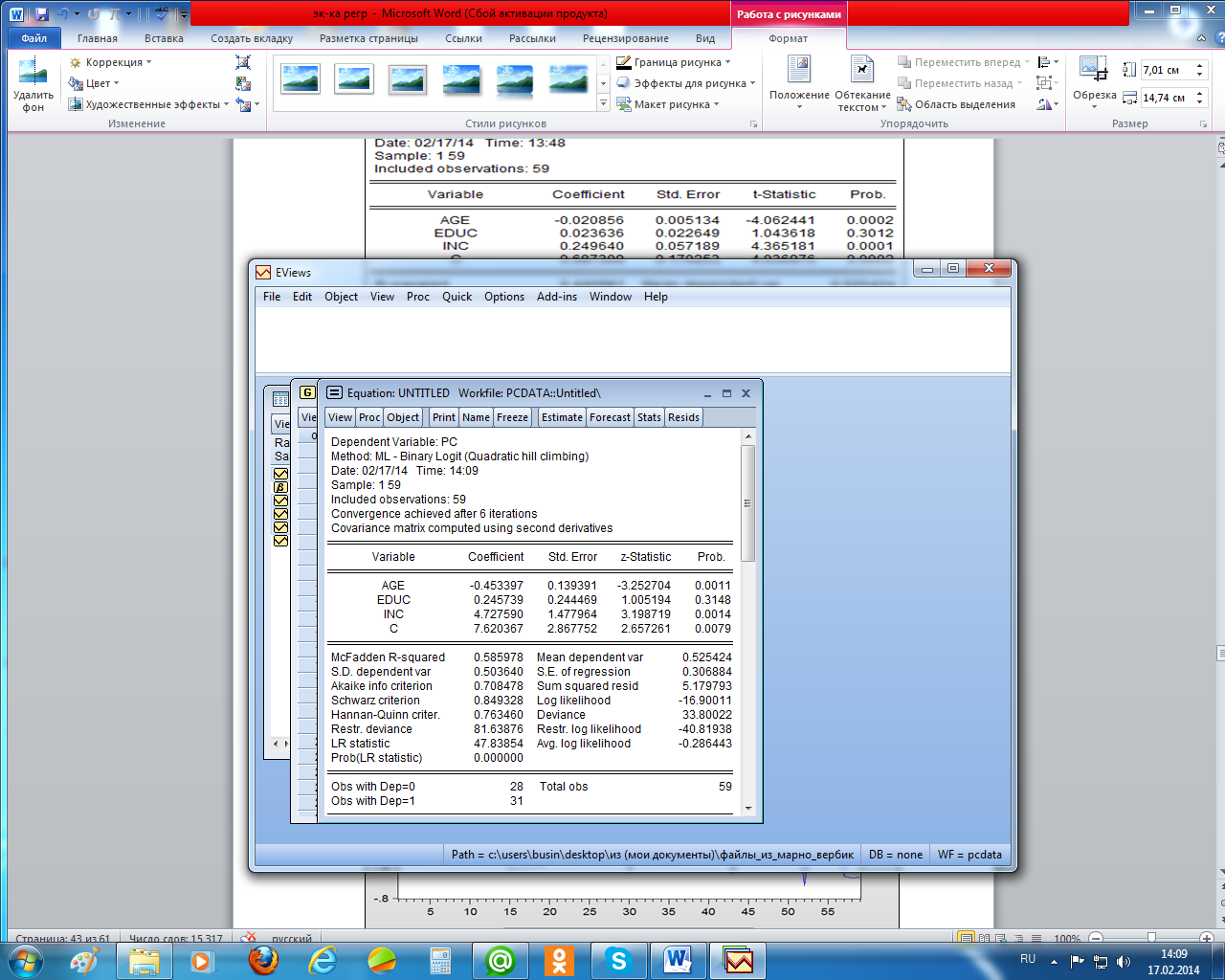
Рисунок 2.29 – Отчёт об оценке модели бинарного выбора
|
|
|
По графикуфактических, расчётных значений и остатков logit- модели (рисунок 2.30) видно, что эта модель более точно описывает переменную отклика и все её значения попали в интервал [0,1]. Так что данную модель можно признать адекватной исходным данным.
Чтобы сравнить коэффициенты при переменных в линейной модели вероятностей и в logit- модели, воспользуемся правилом Амемийя, в соответствии с которым коэффициенты logit- модели надо уменьшить в 4 раза и к константе добавить 0,5. Получим
Константа b1 b2 b3
Logit- модель 2,405  0,113 0,061 1,182
0,113 0,061 1,182
лин. модель вероятностей 0,687  0,021 0,024 0,250
0,021 0,024 0,250
----------------------------------------------------------------------------------------------------- Как видим, все оценки logit- модели больше оценок линейной модели вероятностей.

Рисунок 2.30 – График фактических, расчётных значений и остатков logit -модели
EViews представляет возможность спрогнозировать по оценённой модели вероятность наступления события при фиксированных значениях независимых переменных. Допустим, надо рассчитать вероятность того, что индивид в возрасте 40 лет, проучившийся 5 лет и имеющий доход на уровне 2 (от 20 000 до 30 000) имеет компьютер. Для этого в окне команд надо набрать уравнение оценённой модели и подставить в неё значения независимых переменных Нажав «Enter», получим 0,542. Это и есть оценённая вероятность (рисунок 2.31).

Рисунок 2.31 – Прогноз переменной отклика
По линейной модели вероятностей получим р = 0,687  0,021
0,021  40 + 0,024
40 + 0,024  5 + 0,250
5 + 0,250  2 = 0,467. Здесь различие небольшое. Но если взять более молодого (35 лет) и менее грамотного (образование 1 год) индивида с более высоким доходом (свыше 50 000), то получим, что вероятность иметь компьютер по logit- модели практически равна 1 (рисунок 2.32), а по линейной модели вероятностей равна р = 0,687
2 = 0,467. Здесь различие небольшое. Но если взять более молодого (35 лет) и менее грамотного (образование 1 год) индивида с более высоким доходом (свыше 50 000), то получим, что вероятность иметь компьютер по logit- модели практически равна 1 (рисунок 2.32), а по линейной модели вероятностей равна р = 0,687  0,021
0,021  35 + 0,024
35 + 0,024  1 + 0,250
1 + 0,250  5 = 1,23, что лишено смысла.
5 = 1,23, что лишено смысла.
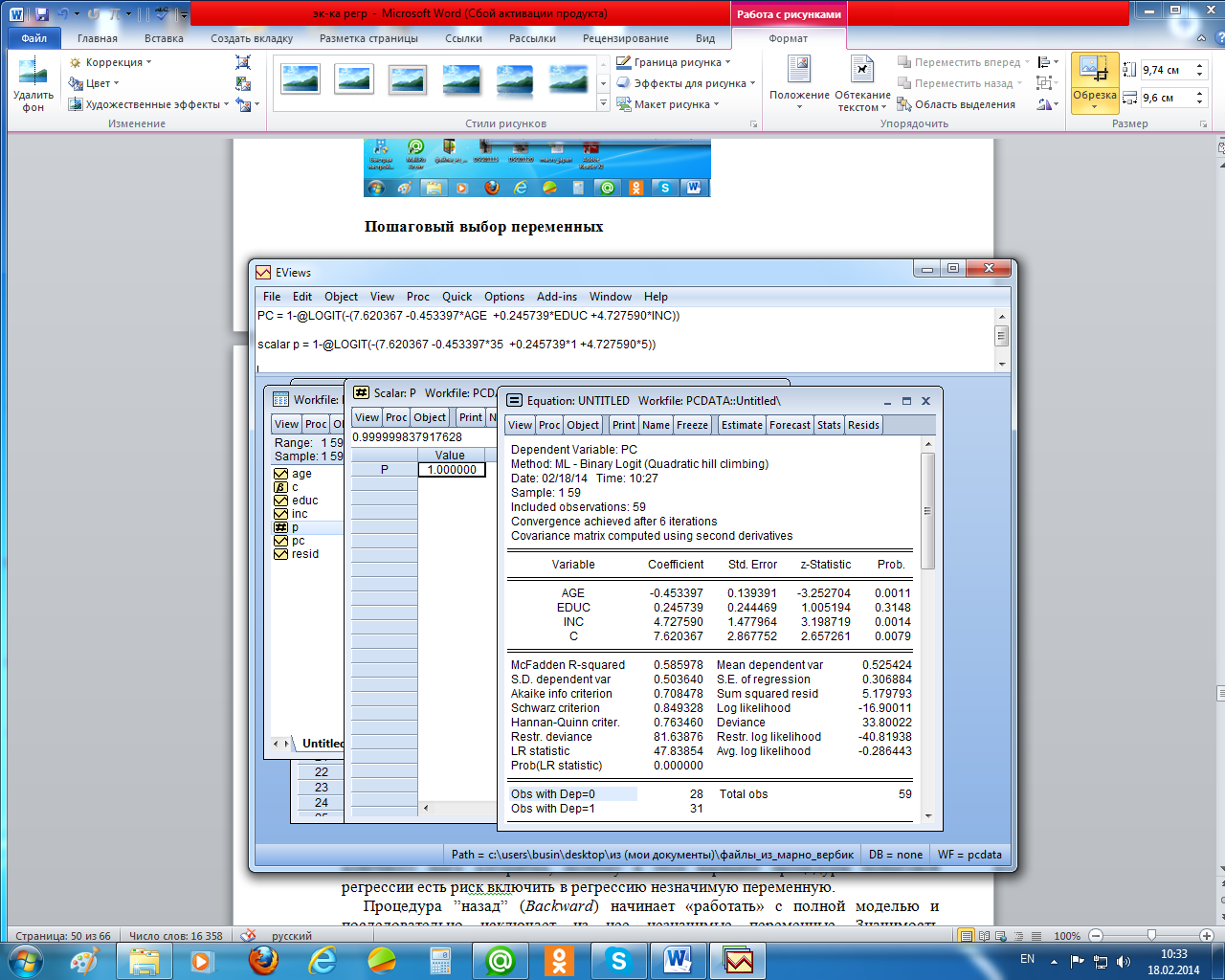
Рисунок 2.32 – Прогноз переменной отклика для других значений независимых переменных
Отметим, что здесь был рассмотрен наиболее простой вариант logit- модели – модель бинарного выбора. В эконометрической литературе можно найти более сложные модели, которые здесь не рассматриваются.
|
|
|
|
|
|


