 |
nпара/nжид = EL/KE = (55-50)/(85 -55 )= 1/6
|
|
|
|
nпара/nжид = EL/KE = (55-50)/(85 -55 )= 1/6
где: nпара ─ число молей пара ( 1 часть), nжид ─ число молей жидкости ( 6 частей) общее количество молей n = 46, 78 моль ( 7 частей). Тогда:
nпара = 46, 78 1/7 = 6, 68 моль
nжид = 46, 78 6/7 = 40, 1 моль ( nжид. = n─ nпар . ). Отсюда, с учетом того, что xi ─ мольные доли компонентов в соответствующих фазах, а Mi ─ их молярные массы, масса компонентов в паре и жидкости ( gi ) вычисляется следующим образом:
· 
|
· 
|
· 
|
· 
|
В сумме получим: 357, 7+1263, 15+18, 04+361, 9=2000 г
4. а) 3аданный массовый состав системы 80 кг HNO3 и 20 кг H2О пересчитывается на мольный состав. Для этого определим число молей каждого компонента в системе:
· 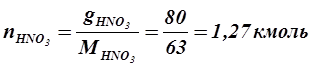
|
· 
|
Тогда мольные доли компонентов в системе:
·  , ,
|
· 
|
Заданный массовый состав соответствует 53мол. % HNO3 и 47мол. % H2О.
б) Так как заданный состав смеси находится слева от азеотропной точки, то выделить ректификацией в чистом виде можно только азотную кислоту. Вся вода ( 1, 11моль )перейдет в азеотропную смесь с молярным содержанием 61, 7мол% Н2О. Остальные 38, 3 мол. % в азеотропном растворе составит азотная кислота. Рассчитаем количество HNO3 в азеотропе, если 

Отсюда: 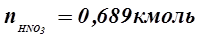
Следовательно, в азеотроп перейдет 0, 689моль азотной кислоты, а в чистом виде можно выделить: 1, 27 - 0, 689 = 0, 581 кмоль, или
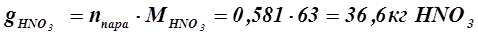
в) Исходная смесь беднее водой, чем азеотропная. Следовательно, необходимо добавлять к системе воду, чтобы получить из исходной смеси азеотропную. Так как добавляется вода, количество азотной кислоты остается без изменений - 1, 27 кмоль. Рассчитывается количество воды в азеотропной смеси:

Отсюда: 
В растворе имеется 1, 11 кмоль воды. Следовательно, добавить необходимо 2, 05 - 1, 11 = 0, 94 кмоль, или 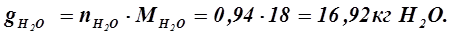
|
|
|
Задача 2
На основании данных о температурах начала и конца равновесной кристаллизации различных по составу сплавов двухкомпонентной системы Сu − Аg, построить диаграмму плавкости указанной системы при постоянном давлении р = 1, 013 105 н/м2.
| Мольн. %Сu | |||||||||
| Т, , Кначала кристаллизации | |||||||||
| Т, К конца кристаллизации |
Определите по диаграмме: при какой температуре начнет кристаллизоваться сплав, содержащий 70 мол. % Сu, каков состав выпавших кристаллов, при какой температуре он закристаллизуется полностью, каков состав исчезающей жидкости? Запишите в виде уравнений схему процесса кристаллизации и зарисуйте его кривую охлаждения, укажите вариантность системы.
Определите по диаграмме: при какой температуре начнется плавление сплава, содержащего 15 мол. % Сu, при какой температуре он полностью расплавится и каков состав исчезающих кристаллов? Покажите на диаграмме стрелками изменение состава фаз в процессе плавления.
Решение :
1. Построение диаграммы
Проведем оси координат и отложим в масштабе по оси ординат температуру, а по оси абсцисс концентрацию. (Если по диаграмме не предполагается делать вычисления, связанные с определением теплоты плавления, то переводить данную в условии концентрацию в мольные доли не обязательно. )
Отмечаем на диаграмме для каждого сплава, указанной концентрации точки температур, соответствующих началу (○ ) и концу 

|
| Рис. 5. 2. |
Соединяем точки конца кристаллизации, учитывая, что температура 1050К остается постоянной вплоть до концентраций 100% и 0%Сu, получаем прямую линию эвтектики.

|
| Рис. 5. 3. |
Соединяем точки начала кристаллизации, экстраполируя левую и правую ветви до пересечения с линией конца кристаллизации в точке эвтектики Е, получаем ветви линий ликвидус.
В результате построена диаграмма плавкости с отсутствием растворимости компонентов в твердом состоянии, (диаграмма с эвтектикой), рис. 5. 3. Обозначим на полученной диаграмме фазовые поля. Точка эвтектики Е найдена геометрическим построением и имеет координаты: ТЕ = 1050К, LE (Сu − 33 моль. %, Аg− 67 моль. % ) .
|
|
|
2. Анализ фазовых превращений
Для определения температуры начала кристаллизации системы, содержащей 70 мольн. % Сu (и 30 мол. % Ag), необходимо найти точку пересечения перпендикуляра, соответствующего данному составу, с линией ликвидус (фигуративную точку f ). Температура, соответствующая этой точке ( 1175К ) и есть температура начала кристаллизации. Согласно данной диаграмме из расплава выпадают кристаллы меди.
Полностью сплав, содержащий 70 мольн. % Сu, закристаллизуется при эвтектической температуре – 1050К. Состав исчезающей жидкости имеет эвтектический состав LE , характеризующийся точкой Е (Сu − 33 моль. %, Аg− 67 моль. % ).
Из этого расплава одновременно кристаллизуются две твердые фазы: медь и серебро в виде твердой эвтектики.
Таким образом, заданный сплав кристаллизуется в две стадии:
1) L→ кр Cu (в интервале температур 1175 − 1050К )
2) LЕ→ кр. Cu + кр Ag (при постоянной температуре 1050К ).
Кривая охлаждения данного сплава представлена на рис. 5. 4.

|
| Рис. 5. 4 |
Вариантность системы, рассчитанная по правилу Гиббса ( С=3-Ф ), для фазовых полей L и кр. Cu +кр. Ag - С=2, для фазовых полей L+кр. Cu и L+кр. Ag – C=1. В первом случае можно менять в определенных пределах оба параметра (состав и температура), во втором случае только один параметр (например, температура) без изменения вида и числа фаз в указанной системе. Состав фаз определяется по линиям ликвидуса и солидуса.
Плавление сплава, содержащего 15 мол. % Cu и, соответственно, 85 мол. % Ag начнется при температуре эвтектики 1050К: появится расплав эвтектического состава LE , соответствующий точке Е (Сu − 33 моль. %, Аg− 67 моль. % ). Это трехфазное превращение кр. Cu + кр Ag → LЕ происходит при постоянной температуре до тех пор, пока не исчезнут все кристаллы меди. Далее температура повышается, плавятся оставшиеся кристаллы серебра кр Ag → L. Полностью они исчезнут при температуре ликвидус: 1120 К.
|
|
|
|
Какой компонент и в каком количестве выкристаллизуется, если 5 кг расплава, содержащего 85мол. % Ag, (диаграмма плавкости на рис. 5. 5) охладить до 1070К?

|
| Рис. 5. 5. |
Решение:
Исходная система при температуре 1070К обозначена на диаграмме точкой О, которая лежит в двухфазной области: L+кр. Ag.
Для определения состава и количества фаз в этой области необходимо через точку О провести конноду ( mn ). Концы этой конноды показывают, что при температуре 1070К система состоит из расплава, состав которого определяется проекцией точки m на ось концентраций (Ag =75 моль. % ), и кристаллов, состав которых определяется проекцией точки n (Ag =100 моль. % ). Таким образом, из расплава кристаллизуется чистое серебро.
Для определения количества кристаллов Ag при температуре 1070К воспользуемся правилом рычага, согласно которому отношение отрезка оm к отрезку nо соответствует отношению количества твердой фазы к количеству расплава.
Так как состав системы Ag − Cu выражен в молярных процентах, то сначала массу исходного расплава ( 5кг ) выразим в киломолях.

|
где: n –число кмолей, соответствующих 5кг расплава,
М1 – молекулярная масса Сu ( 63, 5кг ),
М2 – молекулярная масса Ag ( 108 кг ),
Х 1 – молярная доля Cu ( 0, 15 ),
Х 2 – молярная доля Ag( 0, 85 ).
Обозначим количество выпавших кристаллов Ag при охлаждении исходной системы до 1070К через Y кмоль, а количество расплава – ( 0, 049–Y ) кмоль. Длину отрезков конноды om и no определяем концентрацией одного компонента: Ag.
По правилу рычага:

|
Откуда: Y= 0, 0196 кмоль или масса кристаллов серебра 2, 12 кг.
|
|
|


