 |
Основные формулы для расчета термодинамических характеристик
|
|
|
|
Задача 4
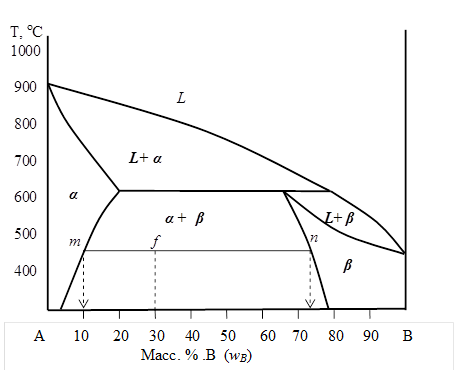
Определите по диаграмме состояния, представленной на рис. 5. 6, какие фазы, какого состава и в каком количественном соотношении будут находиться в равновесии в системе состава wВ=30мас. % при температуре 450оС.
|
| Рис. 5. 6. |
Решение:
Определяем на диаграмме состояния фигуративную точку, соответствующую заданному в условии составу системы при температуре 450оС – это точка f. Данная точка попадает в двухфазную область: α + β , следовательно, при заданных условиях, равновесная система состоит из механической смеси кристаллов двух твердых растворов.
Чтобы определить состав и количественное соотношение α и β фаз, находящихся в равновесии, через точку f необходимо провести конноду − отрезок mn. Составы равновесных фаз определяются проекциями точек m и n на ось концентраций:
состав твердого раствора α: wВ= 10мас. % В и wА = 90мас. % А;
состав твердого раствора β: wВ= 73мас. % В и wА = 27мас. % А.
По заданной концентрационной шкале ( масс. % ) можно найти соотношение масс равновесных твердых растворов gα и gβ . Для этого воспользуемся правилом рычага, согласно которому:
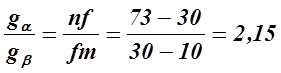
|
Точки n , f и m заданы массовой концентрацией одного компонента В.
Таким образом, в состоянии равновесия в двойной системе А− В, состоящей из 30 мас. % компонента В и 70мас. % - А, при температуре 450оС находятся два твердых раствора α и β , при этом масса твердого α - раствора в системе в 2, 15 раза больше, чем масса твердого β - раствора.
Задача 5
Постройте диаграмму состояния Sn − Bi, по приведенным ниже данным и определите, пользуясь построенной диаграммой:
- теплоту плавления компонента, находящегося в равновесии с раствором содержащим 0, 97мол. дол. Sn (данный расплав считать идеальным раствором),
|
|
|
- активность и коэффициент активности Sn в сплаве, состоящим из 0, 8мол. дол. Sn и 0, 2мол. дол. Bi.
| масс. %Sn | |||||||
| t, oC начала кристаллизации | |||||||
| t, oC конца кристаллизации |
Решение:
Определение теплоты плавления и активности компонента вычисляются при решении подобных задач с помощью уравнений Шредера или Ван-Лаара. Поскольку в этих уравнениях температура измеряется в Т, К, а концентрация задается в мольных долях, то целесообразно сделать перерасчет исходных данных. Мольная доля компонента рассчитывается по формуле:
· 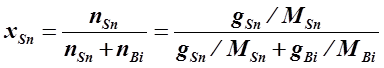
| · |
где: xi – мольная доля компонента,
ni – число молей компонента,
Mi - молярная масса компонента,
gi – масса компонента (обычно расчеты проводят для 100г раствора, в этом случае масса компонента совпадает с его массовым процентом).
Данные для построения диаграммы, полученные в результате перерасчета, указаны ниже:
| Мольн. доляSn (хSn) | 1, 0 | 0, 875 | 0, 725 | 0, 56 | 0, 43 | 0, 24 | |
| Т, К начала кристаллизации | |||||||
| Т, К конца кристаллизации |
1) Построение диаграммы
Температуры плавления чистых компонентов откладываем на осях ординат. Для каждого из приведенных сплавов отмечаем на графике температуры начала и конца кристаллизации растворов.
Точки конца кристаллизации всех сплавов лежат на прямой линии − это линия эвтектики, рис. 5. 7.
Соединив все точки начала кристаллизации, включая температуры плавления чистых компонентов, получим две ветви кривых ликвидус, которые сходятся в точке эвтектики Е.
В результате получаем диаграмму, в которой Sn и Bi кристаллизуются раздельно, не образуя твердых растворов. Это диаграмма с эвтектикой.
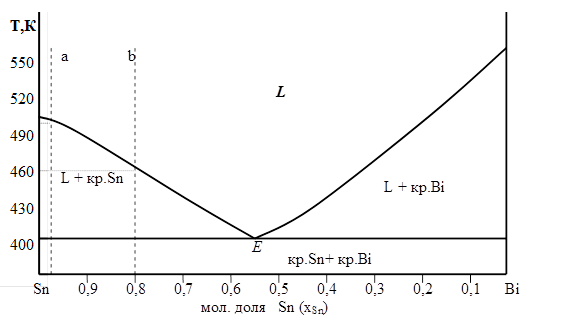
|
| Рис. 5. 7 |
2) Расчет теплоты плавления
|
|
|
В системах с эвтектикой для определения теплоты плавления компонента, находящегося в равновесии с насыщенным раствором, используется уравнение Шредера для идеальных растворов. Расплав состава xSn=0, 97 (отмечен на диаграмме как точка а ), согласно условию, можно считать идеальным.
Согласно диаграмме, заданный насыщенный раствор находится в равновесии с кристаллами олова при температуре, отвечающей линии ликвидус, следовательно, по уравнению ( 5. 3 ) можно определить теплоту плавления олова:
· 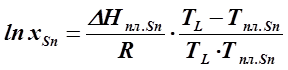
|
где: хSn – мольная доля олова в насыщенном растворе, находящимся в равновесии с кристаллами олова,
ТL – температура, при которой насыщенный раствор данной концентрации хSn находится в равновесии с кристаллами олова или температура начала кристаллизации этого раствора (определяют по диаграмме состояния – 500К ),
Тпл. Sn – температура плавления чистого олова (505К),
Δ Нпл Sn - теплота плавления олова.
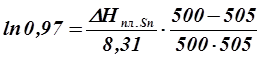
|
Отсюда: Δ НплSn= 12590 Дж/моль
3)Расчет активности и коэффициента активности олова в расплаве.
Расплав состава хSn = 0, 8 (отмечен на диаграмме как точка b) нельзя принять идеальным. Для определения активности олова в этом расплаве используем уравнение Шредера для реальных растворов ( 5. 4 ):
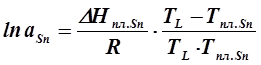 , ,
|
где: а Sn - активность олова в данном расплаве,
ТL – температура начала кристаллизации расплава состава хSn = 0, 8 (определяется по диаграмме состояния – 469К )
Отсюда:
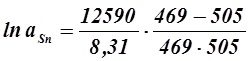 , а Sn = 0, 78 , а Sn = 0, 78
|
Коэффициент активности ( 5. 5 ):
| γ = а Sn / х Sn = 0, 78 / 0, 8 = 0, 98 |
Задача 6
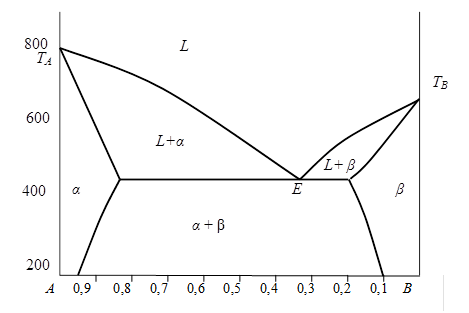
Нарисуйте условную диаграмму плавкости системы А− В, если известно:
- А и В неограниченно растворимы в жидком состоянии;
- температура плавления А: 790К,
- температура плавления В: 630К,
- при температуре 420К имеется нонвариантное превращение, сос-тав жидкой фазы в нонвариантном превращении: хА=0, 35,
- минимальная растворимость компонентов в твердом состоянии составляет: А в В - хА=0, 1; В в А - хВ=0, 05,
- максимальная растворимость компонентов в твердом состоянии: А в В - хА=0, 2; В в А – хВ =0, 15.
Решение:
1. Проводим и масштабируем оси: по оси температур достаточно ограничиться интервалом от 200 до 900 К, ось концентраций размечаем в мольных долях (выбор единиц измерения может быть и иным).
|
|
|
2. Отмечаем температуры плавления чистых компонентов ТА и ТВ.
3. Проводим горизонталь, соответствующую нонвариантному, а следовательно трехфазному превращению при Т=420К и отмечаем на этой горизонтали точку, соответствующую составу жидкой фазы: хА=0, 35. (т. Е ). Эта точка является эвтектической, т. к. расположена ниже температур плавления чистых компонентов.
4. Поскольку ветви ликвидус пересекаются на линии нонвариантного превращения в точке, характеризующей жидкую фазу, соединяем точки ТА и ТВ с точкой Е – получаем линии ликвидус.
5. Минимальную растворимость компонентов в твердом состоянии отобразим на данной диаграмме при наименьшей температуре, поэтому отмечаем на оси концентраций точку хВ=0, 05 – минимальная растворимость В в А и точку хА=0, 1 – минимальная растворимость А в В. Эти точки служат началом линий ограничения растворимости в твердом состоянии.
3. Максимальная растворимость в твердом состоянии соответствует температуре нонвариантного превращения. Поэтому отмечаем на изотерме Т=420К точку хА=0, 2 – максимальная растворимость А в В и точку хВ=0, 15 – максимальная растворимость В в А. Эти точки являются концом линий ограничения растворимости в твердом состоянии.
Соединяем точки минимальной и максимальной растворимости сначала А в В, а затем В в А − получаем две линии ограничения растворимости компонентов.
6. Соединяем точки плавления А и В с концами нонвариантной (эвтектической) горизонтали – получаем линии солидус.
|
| Рис. 5. 8. |
Построенная диаграмма (рис. 5. 8. ) представляет собой диаграмму плавкости эвтектического типа с переменной растворимостью компонентов в твердом состоянии и образованием двух типов граничных твердых растворов: α и β .
Отметим на диаграмме фазовые области: L, L+α, L+β, α, β, α +β .
Задача 7
Нарисуйте условную диаграмму состояния системы А− В по приведенным данным:
- А и В неограниченно растворимы в жидком состоянии,
- температура плавления А–1150К,
|
|
|
- температура плавления В− 950К,
- в системе имеется два химических соединения:
1) А3В2, плавящееся конгруэнтно при Тпл. =1300К,
2) АВ, плавящееся инконгруэнтно при Тразл. =1000К,
- в системе протекают три нонвариантных превращения:
1) при температуре 700 К, состав жидкой фазы хА=0, 7,
2) при температуре 1000 К, состав жидкой фазы хА=0, 4,
3) при температуре 400 К, состав жидкой фазы хА=0, 2,
- компонент В ограниченно растворяется в решетке компонента А и образует граничный твердый раствор с переменной растворимостью от хВ=0, 03 до хВ=0, 15,
- растворимость компонентов А и В в А3В2 отсутствует,
- вблизи химического соединения АВ и компонента В твердых растворов не образуется.
Решение:
Построение диаграммы разумно начинать с анализа химических соединений. Если химическое соединение конгруэнтно плавящееся, т. е. не меняет своего состава вплоть до температуры плавления, то его можно рассматривать как самостоятельный компонент, который позволяет разделить данную диаграмму на более простые. В этом случае на диаграмме проходит вертикальная черта через точку, соответствующую стехиометрическому составу этого соединения, до температуры его плавления и сама диаграмма как бы делится на две.
Согласно условию задачи, таким соединением является А3В2. Согласно стехиометрическим коэффициентам молекулярной формулы в этом соединении компонента А–0, 6 мольн. дол. , а компонента В–0, 4 мольн. дол.
1. Проводим и масштабируем оси ( рис. 5. 9 ). Откладываем на осях значения температуры в К (достаточно ограничиться интервалом от 300 до 1400К ) и состава системы − например, в моль. дол компонента В ( хВ ).
2. Отметим на диаграмме температуры плавления чистых компонентов: ТА=1150К и ТВ=950 К соответственно.
3. Проводим через точку, соответствующую составу конгруэнтного химического соединения: хА=0, 6 и хВ=0, 4 вертикальную черту до температуры плавления данного соединения 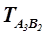 = 1300 К.
= 1300 К.
Далее построение общей диаграммы проводим раздельно: сначала для системы А− А3В2 и затем для системы А3В2− В.
4. В системе А-А3В2 согласно условию имеется нонвариантное превращение при Т=700К и составе жидкой фазы хА = 0, 7 (хВ=0, 3).
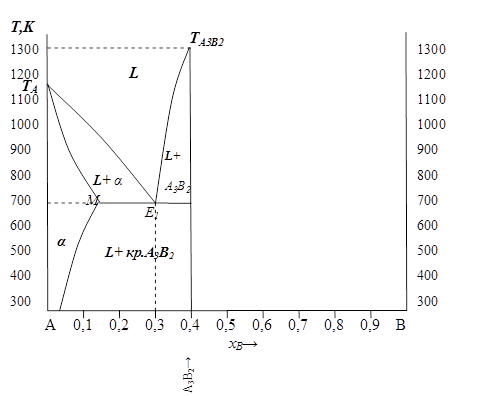
|
| Рис. 5. 9. |
Так как температура нонвариантного превращения ниже обеих температур плавления, то это − эвтектическое превращение. Намечаем эвтектическую горизонталь и отмечаем на ней точку эвтектики Е1, соответствующую составу жидкости при эвтектической температуре ( хВ=0, 3 ).
5. Эвтектика − это точка пересечения ветвей ликвидус, поэтому соединяем ТА с Е1 и 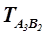 с Е1 и получаем две линии ликвидус.
с Е1 и получаем две линии ликвидус.
6. Согласно условию, вблизи соединения А3В2 не образуется промежуточных твердых растворов, поэтому линия эвтектики почти вплотную подходит к данному соединению (но не пересекает его).
|
|
|
7. Вблизи компонента А образуется граничный твердый раствор. Отметим согласно условию область существования α твердого раствора на основе компонента А.
Как правило, максимальная растворимость в твердом состоянии в системах эвтектического типа наблюдается при эвтектической температуре, поэтому на линии эвтектики отметим точку М, соответствующую максимальной растворимости компонента В в А (поусловию хВ=0, 15 ).
8. Минимальную растворимость компонентов в твердом состоянии отобразим на данной диаграмме при наименьшей температуре, поэтому отмечаем на оси концентраций точку хВ=0, 03 – минимальная растворимость В в А.
9. Соединим точки минимальной и максимальной растворимости – получим линию ограничения растворимости компонента В в А.
10. Соединим ТплА и точку М – получим линию солидус.
11. Таким образом, система А− А3В2 представляет собой диаграмму эвтектического типа с ограниченной растворимостью в твердом состоянии.
Обозначим все области на полученной части диаграммы: слева от линии переменной растворимости и ниже линии солидус – однофазная область существования твердого раствора α , выше линии ликвидус – однофазная область существования жидкого раствора – L, ниже линии эвтектики – двухфазная область существования твердого раствора α и химического соединения А3В2. Между линиями ликвидус и солидус − двухфазные области ( L+α ) и ( L+А3В2 ).
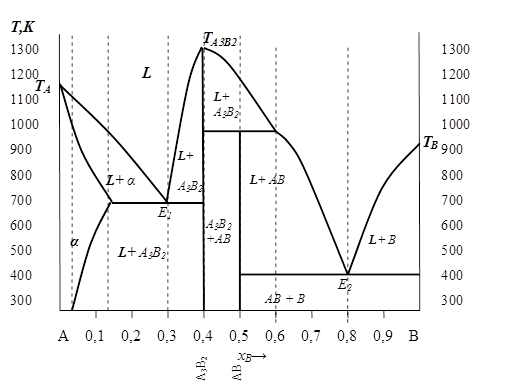
12. Переходим к построению второй части диаграммы состояния: системы А3В2 − В , рис. 5. 10.
Согласно условию, в этой области концентраций имеется инконгруэнтно плавящееся химическое соединение АВ с температурой разложения 1000К. По его стехиометрической формуле определяем, что это соединение состоит из 0, 5мольн. дол. А и 0, 5 моль. дол. В. Проведем через точку, соответствующую данному составу, вертикальную прямую то температуры 1000 К.
13. Так как данное соединение плавится инконгруэнтно, то при температуре 1000К оно разлагается по реакции перитектического превращения, которому должна соответствовать горизонталь нонвариантного превращения на диаграмме состояния. Проведем эту горизонталь от соединения А3В2 до точки Р, соответствующей, согласно условию, составу жидкого перитектического раствора: хА = 0, 4 ( хВ=0, 6 ).
Соединяем 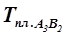 с точкой Р – получаем ветвь линии ликвидус.
с точкой Р – получаем ветвь линии ликвидус.
14. В условии оговорено, что компонент В не растворяется в решетке соединения А3В2, а также вблизи соединения АВ и компонента В нет областей твердых растворов и, следовательно, линии переменной растворимости в твердом состоянии в этой части диаграммы присутствовать не будут.
15. Из условия известно, что при температуре 400К в системе имеется еще одно нонвариантное превращение с составом жидкой фазы 0, 2 мольн. дол. А.
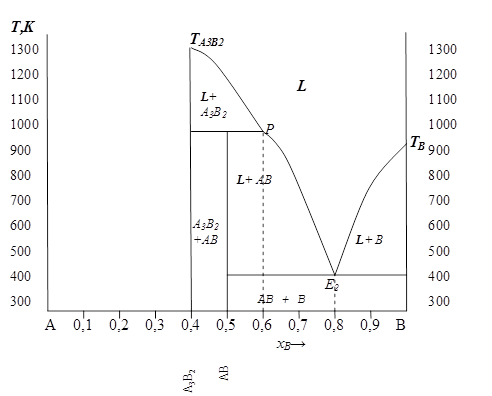
|
| Рис. 5. 10. |
Температура нонвариантного превращения ниже температур плавления твердых фаз ( 1000К – соединение АВ и 950К – компонент В ), следовательно данное нонвариантное превращение является эвтектическим. На диаграмме оно будет представлено горизонтальной линией, проходящей при температуре 400К от фазы АВ до фазы В. Отмечаем на ней точку эвтектики Е2, соответствующую составу жидкой фазы при данной температуре хА=0, 2 ( хВ=0, 8 ).
16. Из точек Р и ТВ опускаем к линии эвтектики две ветви ликвидуса, которые пересекаются в точке эвтектики Е2.
17. На полученной части диаграммы А3В2− В (рис. 5. 10) подписываем все области межфазного равновесия.
Полностью полученная диаграмма представлена на рис. 5. 11.
|
| Рис. 5. 11 |
Задача 8
Построение диаграммы состояния термодинамическим методом проведем на примере двухкомпонентной системы Sn–Bi с эвтектикой.
Компоненты диаграммы Sn–Bi не образуют твердых растворов. При рассмотрении фазового равновесия в заданной двухкомпонентной системе сначала выбираем температуры, при которых определяются составы равновесных фаз.
Далее для каждой из температур необходимо рассчитать концентрационные зависимости свободной энергии Гиббса для всех фаз, присутствующих в системе, построить графики этих зависимостей, провести к ним касательные и графически определить составы сосуществующих в равновесии фаз.
Проекция составов равновесных фаз на изотермы диаграммы Т–х, позволит построить линии двухфазного и трехфазного равновесия.
При проведении расчетов необходимо воспользоваться справочными термодинамическими данными.
Основные формулы для расчета термодинамических характеристик
Cвободные энергии Гиббса чистых компонентов DGSn и DGВi для твердой и жидкой фазы при заданной температуре Т можно рассчитать по приведенным ниже термодинамическим формулам.
Для компонентов в твердой фазе (обозначим ее индексом S ):
| DGoi, T, s = DHoi, T, s – T DSoi, T, s |
(5. 1) | |
| где: DHoi, T, s = DHof, 298, i + ò cpsdT | ||
| и | ||
|
DSoi, T, s = Sof, 298, i + ò (cp, s/T )dT; | ||
Для упрощения расчетов можно принять, что ср , –const и не зависит от температуры. Тогда:
| DHoi, Ts = DHof, 298, i + cps (T-298); | (5. 2) |
| DSoi, Ts = Sof, 298, i + cps ln(T/298) | (5. 3) |
Для компонентов в жидкой фазе (обозначим ее индексом L ):
| DGoi, T, L = DHoi, T, L – T DSoi, T, L; | (5. 4) |
| DHoi, T, L = DHoi, T, s +DHoплавл. i ; | (5. 5) |
| DSoi, T, L = DSoi, T, s + DHoплавл. i / Тплавл. i | (5. 6) |
Изобарно–изотермический потенциал для моля жидкого раствора системы Sn – Bi для заданной температуры определяется согласно:
| DGр-раL =хSn DGSnL + хВi DGВiL + DGсм | (5. 7) |
Предположим, что образующийся раствор является идеальным, тогда изменение свободной энергии смешения DGсм можно определить как:
| DGсм = RT (хSn lnxSn + хВi lnxВi) | (5. 8) |
Таким образом, по приведенным выше уравнениям для некоторой температуры Т, можно рассчитать и далее построить концентрационную зависимость изобарно–изотермического потенциала Gр-раL для идеального жидкого раствора.
В данной двойной системе твердых растворов не образуется, т. е. компоненты кристаллизуются раздельно, поэтому касательная к концентрационной зависимости свободной энергии Гиббса для расплавов проводится из точки DGoi, T, s, характеризующей энергию Гиббса кристаллизующегося чистого твердого компонента.
Термодинамические расчеты для системы Sn – Bi
Для расчетов выберем температуры ниже температур плавления олова и висмута, но выше предполагаемой температуры эвтектики. Например, Т1 =473К и Т2 =443 К.
На основании уравнений (5. 1) – (5. 8) и справочных термодинамических данных: теплот образования веществ, энтропий образования веществ, теплоемкостей и теплот плавления веществ, вычисляем значение свободной энергии Гиббса каждого компонента в твердом и в жидком состоянии, а также концентрационное изменение свободной энергии Гиббса при образовании расплавов.
Справочные материалы для данной системы:
| · Тпл. Sn= 505 K; DHof, 298, Sn=0; cp, 298, Sn=26, 99 Дж/мольК; | |
| · Sof, 298, Sn= 51, 55 Дж/мольК; DHoплавл. Sn=7, 03кДж/моль. | |
| · Тпл. Bi= 544 K; DHof, 298, Bi=0; cp, 298, Bi=26, 02 Дж/мольК; | |
| · Sof, 298, Bi= 56, 9 Дж/мольК; DHoплавл. Bi=12, 180кДж/моль. |
Расчеты для температуры 473 К
| · (Sn): DHos, T, Sn =26, 99(473-298)=4723, 25 Дж/моль; |
| · DSos, T, Sn = 51, 55 + 26, 99 ln(473/298)=64, 01Дж/мольК |
| · DGos, T, Sn = 4723, 25 – 473. 64, 01 = -25553, 48Дж/моль; |
| · DHoL, T, Sn = 4723, 25 + 7030 = 11753, 25 Дж/моль; |
| · DSoL, T, Sn = 64, 01 + 7030/505 = 77, 93 Дж/мольК; |
| · DGoL, T, Sn = 11753, 25 – 473. 77, 93 = -25108, 01Дж/моль; |
| · (Bi): DHos, T, Bi =26, 02(473-298)=4553, 5 Дж/моль; |
| · DSos, T, Bi = 56, 9 + 26, 02 ln(473/298)=68, 92Дж/мольК; |
| · DGos, T, Bi= 4553, 5 – 473. = -28044, 43 Дж/моль; |
| · DHoL, T, Bi = 4553, 5 + 12180 = 16733, 5 Дж/моль; |
| · DSoL, T, Bi = 68, 92 + 12180/544 = 91, 31Дж/мольК; |
| · DGoL, T, Bi = 16733, 5 – 473. 91, 31 = -26456, 00 Дж/моль; |
Вычисляем значение свободной энергии Гиббса расплавов различного состава по уравнениям (5. 7) и (5. 8) при 473К:
Результаты вычислений приведены в табл. 5. 1.
Таблица 5. 1
| хSn | 1, 0 | 0, 9 | 0, 8 | 0, 7 | 0, 6 | 0, 4 | 0, 3 | 0, 2 | 0, 1 | |
| xBi | 0, 1 | 0, 2 | 0, 3 | 0, 4 | 0, 6 | 0, 7 | 0, 8 | 0, 9 | 1, 0 | |
| Gр-раL Дж/моль | -25108 | -26518 | -27344 | -27914 | -28292 | -28562 | -28454 | -28153 | -27597 | -26456 |
Строим кривую концентрационной зависимости Gр-раL для расплавов (рис. 5. 12 кривая 1 ). Так как олово и висмут кристаллизуются раздельно, не образуя твердых растворов, значения DGos, T, Sn и DGos, T, Bi откладываем на графике на осях для соответствующих чистых компонентов. Определяем точки равновесия твердой и жидкой фазы. Для этого из точек DGos, T, Sn и DGos, T, Bi проводим касательные к полученной кривой 1. Точка касания а дает состав насыщенного жидкого раствора, находящегося в равновесии с кристаллическим оловом при температуре 473К и точка в соответствует составу насыщенного расплава, находящемуся в равновесии с кристаллическим висмутом при температуре 473К. Далее проецируем эти составы на диаграмму состояния Т–х на изотерму Т1=473К ( рис. 5. 13 ) . Это точки линии ликвидус.
Расчет для температуры 443 К проводим аналогично.
Вычисляем значение свободной энергии Гиббса чистых компонентов и образующихся расплавов:
| · (Sn): DHos, T, Sn =26, 99(443-298)=3913, 55 Дж/моль; | |
| · DSos, T, Sn = 51, 55 + 26, 99 ln(443/298)=62, 25 Дж/мольК; | |
| · DGos, T, Sn = 3913, 55 – 443. 62, 25 = -23663, 88 Дж/моль; | |
| · DHoL, T, Sn = 3913, 55 + 7030 = 10943, 55 Дж/моль; | |
| · DSoL, T, Sn = 62, 25 + 7030/505 = 76, 17 Дж/мольК; | |
| · DGoL, T, Sn = 10943, 55 – 443. 76, 17 = -22800, 11Дж/моль; | |
| · (Bi): DHos, T, Bi =26, 02(443-298)=3772, 9 Дж/моль; | |
| · DSos, T, Bi = 56, 9 + 26, 02 ln(443/298)= 67, 22Дж/мольК; | |
| · DGos, T, Bi= 3772, 9 – 443. 67, 22 = -26004, 20Дж/моль; | |
| · DHoL, T, Bi = 3772, 9 + 12180 = 15952, 9 Дж/моль; | |
| · DSoL, T, Bi = 67, 22 + 12180/544 = 89, 61Дж/мольК; | |
| · DGoL, T, Bi = 15952, 9 – 443. 89, 61 = -23744, 20Дж/моль; |
Вычисляем значение свободной энергии Гиббса расплавов различного состава при Т=443К:
Результаты вычислений приведены в табл. 5. 2:
| хSn | 1, 0 | 0, 9 | 0, 8 | 0, 7 | 0, 6 | 0, 4 | 0, 3 | 0, 2 | 0, 1 | |
| xBi | 0, 1 | 0, 2 | 0, 3 | 0, 4 | 0, 6 | 0, 7 | 0, 8 | 0, 9 | 1, 0 | |
| Gр-раL Дж/моль | -22800 | -24089 | -24831 | -25333 | -25655 | -25844 | -25710 | -25397 | -24844 | -23744 |
Таблица 5. 2
Строим кривую концентрационной зависимости Gр-раL для расплавов при Т=443К( рис. 5. 13 кривая 2 ). Так как олово и висмут кристаллизуются раздельно, не образуя твердых растворов, значения DGos, T, Sn и DGos, T, Bi откладываем на графике на осях для соответствующих чистых компонентов. Определяем точки равновесия твердой и жидкой фазы. Для этого из точек DGosT, S n и DGosT, Bi проводим касательные к полученной кривой 2. Точка касания а1 дает состав насыщенного жидкого раствора, находящегося в равновесии с кристаллическим оловом при температуре 443К и точка в1 соответсвует составу насыщенного расплава, находящемуся в равновесии с кристаллическим висмутом при температуре 443К. Далее проецируем эти точки на диаграмму состояния Т–х на изотерму Т2=443К (рис. 5. 13). Это точки линии ликвидус.
Аналогичные расчеты и построения можно провести и для других температур. Энергия Гиббса с ростом температуры уменьшается, так как (¶G/¶T)p=-S, поэтому, чем выше температура, тем ниже располагаются кривые (Gр-ра–хi).
На диаграмме состояния Т–х проводим через точки Тплав. Sn, а, а1 и Тплав. Bi, в, в1 ветви линии ликвидус. Они пересекаются и дают эвтектическую точку, лежащую на горизонтальной линии эвтектики.
Необходимо отметить, что в данном случае речь идет не о строгом расчете (было сделано допущение об идеальности образующегося расплава и не учтена температурная зависимость теплоемкости), а о построении принципиальной схемы, отражающей фазовые взаимоотношения в рассматриваемой системе, при условии, что общий характер взаимодействия в системе в принципе известен. Возможны, поэтому, некоторые несовпадения расчетной и экспериментальной диаграмм состояния.
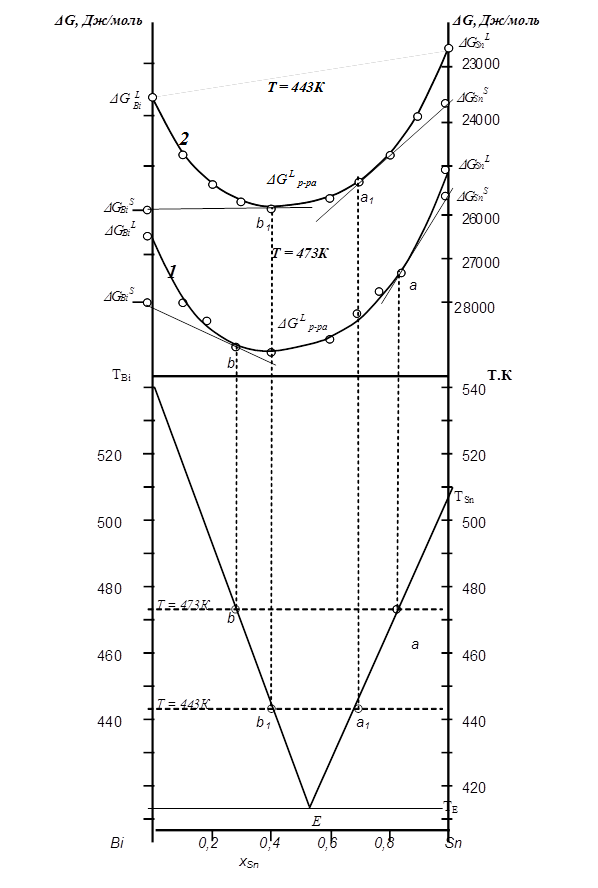
|
| Рис. 5. 13 |
|
|
|


