 |
Тестирование имитационной модели
|
|
|
|
Когда составлена программа моделирования, её проверяют с помощью тестов, т.е. решая задачи с заранее известными ответами.
Пошаговое тестирование состоит в проверке правильности выполнения алгоритма по шагам. В простых случаях можно рассчитать значения переменных для нескольких первых шагов и убедиться, что ЭВМ выдаёт те же значения. В более сложных случаях можно ограничиться выводом значений переменных для первых шагов и анализом этих данных с позиций здравого смысла. Например, если оказалось, что приборы принимают заявки на обслуживание, но ни на одном шаге не происходит освобождение прибора, значит, явно где-то ошибка. Для наглядности можно строить временные диаграммы, демонстрирующие изменения состояний приборов во времени, изменение числа заявок в системе и т.п.
Наряду с пошаговым тестированием необходимо проводить статистическое тестирование хотя бы потому, что никаким пошаговым тестированием не проверить программу генерирования случайных чисел. Если датчик случайных чисел не обеспечивает нужного закона распределения, то оценка оказывается смещённой даже при правильном её построении и правильном алгоритме имитации. Статистическое тестирование проводится путём сравнения полученного значения оценки о точным значением оцениваемой характеристики, найденным теоретическим путём. Так как оценка имеет случайный характер, точного совпадения не будет. Насколько сильно должна отклониться оценка от точного значения, чтобы разница была признана недопустимой и потребовалось выяснение причины такого отклонения? Ответ зависит от назначенного коэффициента доверия. Наиболее распространённым в практике значением коэффициента доверия является 0.95. При этом пороговым значением при принятии решения является величина 2. При таком пороге в пяти процентах случаев (более точно – 4.5%) отклонение, превысившее порог, будет вполне естественным, а отрицательный результат теста будет фактически «ложной тревогой». Но в подавляющем большинстве случаев (95.5%) отклонение, превышающие 2, всё же говорит о каком-то неблагополучии. Обнаружив такое отклонение, надо, прежде всего, получить ещё одну выборку и убедиться, что тревожный предыдущий результат не был ложной тревогой. Если снова отклонение окажется недопустимо большим, значит либо тестовые данные (точное значение) ошибочны, либо программа моделирования выдаёт неправильные оценки. Надо выяснить причину. Подготовка тестовых данных при моделировании СМО требует значения теории массового обслуживания. Приведём без доказательства простой способ расчёта тестовых данных, который пока отсутствует в учебниках и книгах по теории массового обслуживания. Изложить его проще всего на конкретном примере.
|
|
|
Пример. Рассматривается СМО с тремя приборами и двумя ячейками буфера. Имеется пять источников заявок одного типа. Интервал между заявками отельного источника распределён по экспоненциальному закону со средним значением Т. Время обслуживания заявки распределено тоже по экспоненциальному закону, но со средним значением Т0.
На рис. 8.1 изображён граф, отражающий возможные состояния СМО и переходы из одного состояния в другое. Цифра в кружочке указывает текущее количество заявок в системе. Это и есть характеристика состояния СМО. Например, в состоянии 4 заняты все три прибора и одна ячейка буфера. В состоянии 2 заняты два прибора; поскольку один прибор свободен, буфер, естественно, пуст.
На дугах указаны интенсивности переходов, где =1/T- интенсивность потока заявок одного источника, =1/T0- интенсивность обслуживания. Предполагается, что источники заявок имеют конечную ёмкость, равную
|
|
|
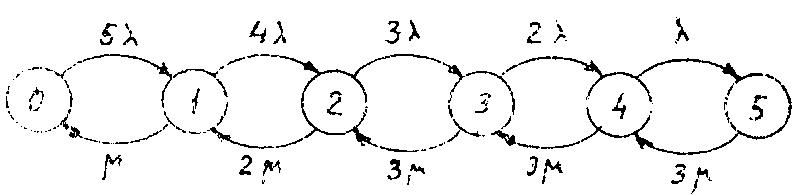
Рис.8.1. Граф состояния СМО.
единице. Это означает, что источник, выдав заявку, оказывается пустым и ждёт, пока его заявка вернётся в этот источник по окончании обслуживания. После возврата заявки в источник она вновь выдаётся через случайный интервал времени, распределение которого указано выше. При единичной ёмкости источника под интервалом между заявками следует понимать время от возврата заявки в источник до выдачи заявки. Это как бы время, требующееся для подготовки очередной заявки. При бесконечной ёмкости источника время подготовки заявки совпадает с интервалом между заявками.
В состоянии 0 в каждом из пяти источников находится по одной заявке, любой из них может выдать заявку, поэтому интенсивность перехода 0®I равна 5. По мере увеличения числа заявок в системе обслуживания уменьшается число источников, содержащих заявку, поэтому интенсивности переходов, связанных с выдачей заявки, уменьшается от 5 до . В случае, когда источники обладают бесконечной ёмкостью, на всех дугах, идущих слева направо, будут интенсивности 5.
Дуги нижнего ряда связаны с переходами, обусловленными окончанием обслуживания заявок. Например, в состоянии 4, когда заняты три прибора (четвёртая заявка находится в буфере), любой из трёх приборов может завершить обслуживание заявки, поэтому интенсивность перехода 4®3 равна 3. В состоянии 2 заняты только два прибора, поэтому интенсивность перехода 2®1 равна 2.
Вычисление вероятностей состояний применительно к установившемуся режиму работы легко осуществляется по графу состояний. Для каждой вершины вычисляются величины, которые назовём индексами и обозначим А. Чтобы вычислить Аi –индекс i-й вершины, надо выделить подграф, состоящий из путей, ведущих к этой вершине. Подграф должен содержать по одной дуге, выходящей из каждой вершины, кроме корневой, т.е. i-й. Примеры подграфов приведены на рис.8.2. Для наглядности обозначены только корневые вершины.
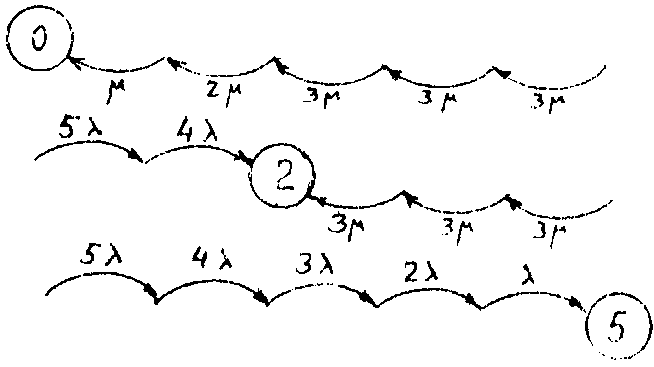
Рис.8.2. Подграфы для вычисления индексов вершин.
Индекс вершины вычисляется как произведение интенсивностей, указанных на дугах подграфа. Индексы вершин для данного примера следующие:
|
|
|
А0=*2*(3)3, А3=5*4*3*(3)2, А1=5*2*(3)3,
А4=5*4*3*2*3, А2=5*4*(3)3, А5=5*4*3*2*,
При небольшом навыке можно сразу написать формулы для индексов, глядя на исходный граф и мысленно выделяя пути, ведущие к корневой вершине. Следует предупредить, что для графов более сложной структуры (имеющих ответвления, перескоки дуг через соседние вершины и т.д.) методика вычисления индексов вершин иная и требует отдельного описания.
Вероятность того, что в произвольный момент времени в системе находится i заявок, вычисляется по формуле:

По вероятностям Рi можно вычислить целый ряд характеристик СМО. Приведём примеры. Вероятность того, что все приборы заняты, равна Р3+Р4+Р5. Вероятность того, что буфер пуст, равна Р0+Р1+Р2+Р3. Коэффициент загрузки прибора равен Кзп = (Р1+Р2*2+(Р3+Р4+Р5)*3)/3.
Коэффициент загрузки буфера Кзп = Р4+Р5*2)/2. Вероятность потери заявки равна Р5, так как при экспоненциальных законах распределения она совпадает с вероятностью полной занятости. При других законах распределения это не так. Следует помнить, что описанная методика расчета вероятностей состояний верна только при экспоненциальных законах распределения интервалов между заявками и длительностей обслуживания.
Рассмотрим пример статистического тестирования. Допустим, были получены выборочные значения оценки вероятности потери заявки в результате моделирования двухканальной СМО с отказами при экспоненциальных законах распределения: 0.204, 0.197, 0.192, 0.226, 0.192, 0.177, 0.206, 0.191, 0.199, 0.182. Воспользуемся описанной методикой, чтобы подсчитать точное значение вероятности потери заявки Рпот для этого случая.

Рис. 8.3. Граф состояний двухканальной СМО.
По графу состояний (рис.7.3) нетрудно написать индексы вершин
А0=22, А1=2, А2=2.
Отсюда находим вероятность полной занятости Р2, которая совпадает с вероятностью потери заявки Рпот, так как в этом примере законы экспоненциальные
|
|
|
Рпот=Р2=А2/(A0+A1+A2)=2/(22+2+2).
Математические ожидания Т и Т0 задавались равными единице, поэтому обратные им значения интенсивностей и тоже равны единице. Подставляя ==1 в формулу, находим Рп=0.2.
В качестве оценки 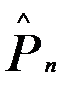 примем среднее арифметическое приведённых выше десяти оценок,
примем среднее арифметическое приведённых выше десяти оценок, 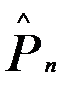 =0.197. Оценка среднеквадратического отклонения
=0.197. Оценка среднеквадратического отклонения 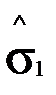 =0.014. Учитывая, что среднее из десяти значений имеет среднеквадратическое отклонение в
=0.014. Учитывая, что среднее из десяти значений имеет среднеквадратическое отклонение в 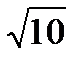 раз меньше, чем каждое из значений, получаем = 1/
раз меньше, чем каждое из значений, получаем = 1/ 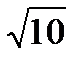 »0.004. Видим, что отличие оценки от точного значения
»0.004. Видим, что отличие оценки от точного значения 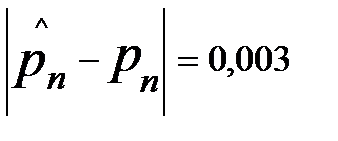 , не превысило , а допускается 2. Следовательно, тест прошёл успешно.
, не превысило , а допускается 2. Следовательно, тест прошёл успешно.
Один успешно закончившийся тест ещё не свидетельствует о правильности программы моделирования. Как хорошо известно, исчерпывающее тестирование вообще невозможно, так что абсолютно уверенно утверждать, что программа правильна, нельзя никогда. Однако степень уверенности в правильности программы возрастает с каждым успешно проведённым тестом. В то же время достаточно одного неудачно завершившегося теста, чтобы перестать доверять выдаваемым программой результатам и приступить к выяснению причины несоответствия. Нередко отрицательный результат тестирования объясняется простой невнимательностью: в программу введены исходные данные, не соответствующие тем, при которых вычислялось точное значение.
Одной из возможных причин неудачного тестирования может быть отличие характеристик последовательности случайных чисел от требуемых. Экспоненциально распределённые случайные числа получаются из базовых случайных чисел. Базовые случайные числа должны быть равномерно распределены в интервале [0,1] и некоррелированы.
Вопросы и задания:
1. Почему пошаговое тестирование необходимо дополнить статистическим тестированием?
2. Почему при статистическом тестировании необходимо осуществлять не один прогон программы, а несколько, хотя бы десяток?
3. Во сколько раз разница между оценкой и точным значением может превышать среднеквадратическое отклонение оценки, чтобы эта разница ещё считалась допустимой?
ПЛАНИРОВАНИЕ СТАТИСТИЧЕСКОГО ЭКСПЕРИМЕНТА
Задача планирования. Пусть X =(x 1,..., xk) - вектор случайных величин, имеющий распределение РХ. Во многих случаях цель статистического эксперимента может быть сведена к определению математического ожидания с.в. y = g (X), где g (X) - заданная функция распределения с.в. X. Типовая схема статистического эксперимента имеет следующий вид (рис. 9.1).
Здесь оценка 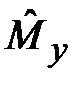 приближается к точному значению M (y) с ростом числа опытов n. Задача планирования статистического эксперимента состоит в нахождении такого n, при котором достигается заданная точность оценки
приближается к точному значению M (y) с ростом числа опытов n. Задача планирования статистического эксперимента состоит в нахождении такого n, при котором достигается заданная точность оценки 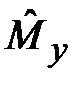 .
.
|
|
|
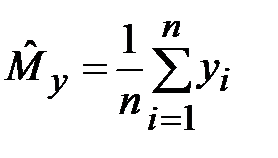
|
| g(X) |
| Xi |
| yi |
| i = 1... n |
Рис. 9.1. Типовая схема статистического эксперимента:
Xi ~ PY; Xi = (x 1 i ,..., xki);
yi - значение с.в. Y в i -м опыте;
n - число опытов
Теоретическое решение задачи планирования. Оценка 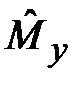 является случайной величиной, так как представляет собой функцию от случайных величин:
является случайной величиной, так как представляет собой функцию от случайных величин:
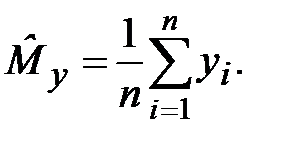 (9.1)
(9.1)
В типовой схеме статистического эксперимента (рис. 3.17) используются независимые реализации xi, поэтому с.в. yi в формуле (9.1) также независимы. Из центральной предельной теоремы вытекает, что с.в. 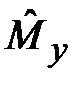 в (9.1) при больших n имеет нормальное распределение, т.е.
в (9.1) при больших n имеет нормальное распределение, т.е.  Определим параметры этого распределения:
Определим параметры этого распределения:
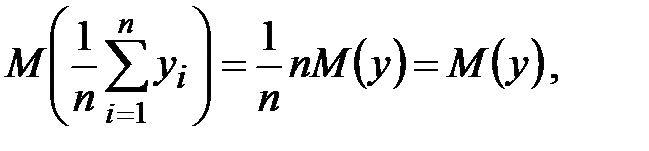 (9.2)
(9.2)

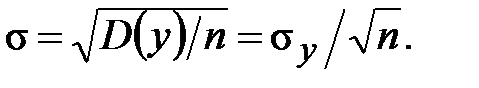 (9.3)
(9.3)
Таким образом, при увеличении числа опытов на порядок s уменьшается в 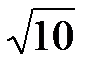 »3 раза. На рис. 9.2. схематически показан вид распределения оценки
»3 раза. На рис. 9.2. схематически показан вид распределения оценки 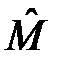 в зависимости от n.
в зависимости от n.
| f (t) |
| M (y) t |
| n =100 n 0 |
| n =10 n 0 |
| n = n 0 |
Рис. 9.2. Распределение с.в. 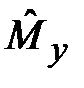 в зависимости от n
в зависимости от n
Диапазон вероятных отклонений оценки от точного значения M (y) сужается пропорционально 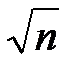 . Параметр s используют как показатель точности оценки. Поскольку
. Параметр s используют как показатель точности оценки. Поскольку 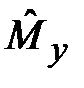 имеет нормальное распределение, то практически достоверно, что
имеет нормальное распределение, то практически достоверно, что 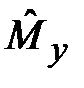 отклоняется от искомого M (y) не более чем на 3s. Можно сказать, что s является аналогом абсолютной погрешности, а 3s - самой абсолютной погрешностью. В качестве аналога относительной погрешности для с.в.
отклоняется от искомого M (y) не более чем на 3s. Можно сказать, что s является аналогом абсолютной погрешности, а 3s - самой абсолютной погрешностью. В качестве аналога относительной погрешности для с.в. 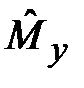 можно рассматривать ее коэффициент вариации:
можно рассматривать ее коэффициент вариации:
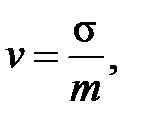
а в качестве самой относительной погрешности - величину 3 v. Из (9.2) и (9.3) находим, что
 (9.4)
(9.4)
где vy - коэффициент вариации с.в. y.
Соотношения (9.3) и (9.4) показывают, что "абсолютная погрешность" - 3s и "относительная погрешность" - 3 v оценки  убывают пропорционально
убывают пропорционально 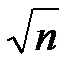 .
.
Из формулы (9.3) находим решение задачи планирования: для достижения заданной точности s требуется n опытов
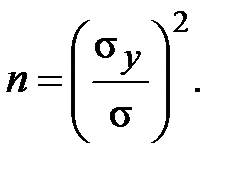 (9.5)
(9.5)
Если требование к точности задано в форме коэффициента вариации v, то требуемое число опытов определяется из формулы (9.4) в виде:
 (9.6)
(9.6)
В решении (9.5) кроме заданного s для определения n необходимо знать s у, в варианте (9.6) - коэффициент вариации vу. Ни то, ни другое до эксперимента, как правило, не известно. Поэтому планирование числа опытов на практике осуществляется в ходе самого статистического эксперимента. Достаточно удобными методами такого планирования являются метод автоостанова.
Метод автоостанова. Схема статистического эксперимента с автоостановом изображена на рис. 9.3. Покажем на примере достижения точности v =0,01.
Как видно из рисунка, в ходе эксперимента ведется непрерывный контроль за оценкой v ' коэффициента вариации v. Когда оценка v' устойчиво входит в зону v '<0,01, эксперимент завершается.
Устойчивое достижение неравенства v '< 0,01 здесь обеспечивается требованием, чтобы это неравенство было подтверждено A =10 раз.
Заметим, что минимальное начальное значение счетчика подтверждений на рис. 9.3, задаваемое в начале алгоритма, должно составлять A =2, так как необходимо исключить одно ложное подтверждение, которое имеет место при n =1. Действительно, при n =1 оценка дисперсии равна нулю, поэтому получается v '=0. При A =10 получится несколько "лишних" повторений цикла. Однако так как n обычно составляет десятки тысяч, то увеличение его на несколько лишних единиц не имеет существенного практического значения.
| n = 1, A = 10 S 1 = 0, S 2 = 0 |
| y=g (X) S 1= S 2+ y S 2= S 2+ y |
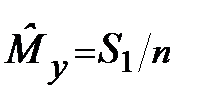 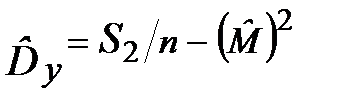 
|
| Генератор с.в. Х |
| Конец |
Печатать 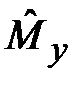 , , 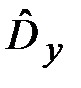 , n , n
|
| A = 0 |
| v’ <0,01 |
| A=A- 1 a |
| Да |
| Нет |
| Начало |
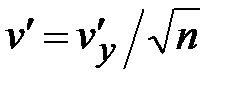
|
| Нет |
| Да |
Рис. 9.3. Схема эксперимента с автоостановом
Как видно из ИСнка, в ходе эксперимента ведется непрерывный контроль за оценкой v' коэффициента вариации v. Когда оценка v' устойчиво входит в зону v' < 0.01, эксперимент завершается.
Устойчивое достижение неравенства v' < 0.01 здесь обеспечивается требованием, чтобы это неравенство было подтверждено A = 10 раз.
Заметим, что минимальное начальное значение счетчика подтверждений на рис. 9.3., задаваемое в начале алгоритма, должно составлять A = 2, т.к. необходимо исключить одно ложное подтверждение, которое имеет место при n = =1. Действительно, при n = 1 оценка дисперсии равна нулю, поэтому получается v' = 0. При A = 10 получится несколько "лишних" повторений цикла. Однако, так как n обычно составляет десятки тысяч, то увеличение его на несколько лишних единиц не имеет существенного практического значения.
Вопросы и задания
1. От каких величин зависит требуемое число опытов? Откуда берутся
их численные значения?
2. Во сколько раз надо увеличить число опытов, чтобы снизить погрешность в 10 раз?
3. Приведите алгоритм моделирования отдельных случайных событий.
4. Приведите алгоритм генерирование зависимых случайных событий.
5. Какие методы тестирования датчиков БСВ Вы знаете? Приведите примеры.
6. Как можно оценить коэффициент корреляции с.в.? Что он показывает?
7. Перечислите характеристики, которыми задается генератор заявок.
8. Раскройте суть метода Монте-Карло.
9. Каким образом реализуется приоритетное обслуживание заявок?
10. Объясните, каким образом решается задача планирования статистического эксперимента.
11. Какими методами может быть оценена точность результатов моделирования?
12. Объясните каким образом осуществляется моделирование сложных случайных событий.
13. Объясните схему статистического эксперимента с автоостановом, изображенную на рис. 9.3.
Планирование машинных экспериментов с моделями систем
Методы планирования эксперимента на модели.
Основная задача планирования– получение необходимой информации при минимальных или ограниченных затратах машинных ресурсов (машинного времени, памяти и т.п.) на реализацию процесса моделирования.
Отличие от натурных экспериментов:
1) простота повторных условий эксперимента на ЭВМ с моделью 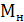 системы S;
системы S;
2) возможность управления экспериментом с моделью 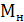 (прерывание, возобновление);
(прерывание, возобновление);
3) легкость варьирования условий проведения экспериментов (воздействий внешней среды, параметров и структуры модели);
4) трудности, связанные с определением интервала моделирования, наличие корреляции между последовательностью случайных чисел в процессе моделирования.
| Модель |

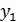
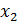
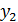
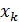
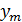
Рис. 10.1. Схема эксперимента
В планировании эксперимента (ПЭ) различают входные (изогенные) и выходные (эндогенные) переменные: х1, х2,…, хк; y1, y2…, ye (рис.1). Входные переменные в теории ПЭ называют факторами а выходные — реакциями.
Каждый фактор x i, i =1,2,…,k может принимать в эксперименте одно или несколько значений, называемых уровнями.
Каждому фиксированному набору уровней факторов точка в факторном пространстве.
Реакцию (отклик) системы можно представить в виде зависимости
y l =Y l (x1, x2,…,xk); l =1…m. Функцию Y l, связанную с факторами, называют функцией отклика, а её геометрический образ – поверхностью отклика. Исследователю заранее не известен вид зависимостей Y l, l =1…m, поэтому используют приближение соотношения:
Зависимости Y l находятся по результатам эксперимента (по существу – это цель эксперимента).
Факторы при проведении эксперимента могут быть:
– управляемыми и неуправляемыми,
– количественными или качественными,
– фиксированными и случайными,
– изучаемыми и неизучаемыми,
– фиксированными и случайными
Фактор относится к изучаемым, если он включён в модель для изучения свойств системы. Количественными факторами являются интенсивности входящих потоков заявок, интенсивности потоков обслуживания, ёмкости накопителей, количество обслуживающих каналов и другие. Качественным факторам не соответствует числовая шкала (дисциплины постановки на очередь, обслуживания).
Фактор является управляемым, если его уровни целенаправленно выбираются экспериментатором.
При планировании эксперимента обычно изменяются несколько факторов.
Основными требованиями, предъявляемыми к факторам - независимость и совместимость. Совместимость означает, что все комбинации факторов осуществимы.
Для выявления влияния факторов на искомые характеристики необходимо:
– отобрать факторы  , i =
, i = 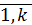 , влияющие на искомую характеристику, и описать функциональную зависимость (делаем, когда строим модель);
, влияющие на искомую характеристику, и описать функциональную зависимость (делаем, когда строим модель);
– установить диапазон изменения значений факторов 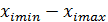 ;
;
– определить координаты точек фазового пространства 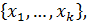 в которых следует проводть эксперимент;
в которых следует проводть эксперимент;
– оценить необходимое число реализаций и их порядок в эксперименте.
Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом.
Практика показывает, что для получения достаточно точных оценок можно обойтись малым количеством опытов, вводя понятие дробного факторного эксперимента (или дробных реплик), который представляет собой некоторую часть (1/2, 1/4, 1/8, и т. д.) от полного факторного эксперимента.
Различают стратегическое и тактическое планирование машинных экспериментов с моделями систем.
Стратегическое планирование ставит своей целью получение необходимой информации о системе S с помощью модели MM, реализованной на ЭВМ.
Тактическое планирование – определяет способы проведения каждой серии испытаний машинной модели MM.
Стратегическое планированиележит в основе разработки плана. Основные проблемы, которые приходится решать: большое количество факторов (сокращение факторного пространства); многокомпонентность функции реакции; стохастическая сходимость результатов машинного эксперимента; ограниченность машинных ресурсов.
Проблема стохастической сходимости результатов машинного эксперимента. Выходные характеристики – выборочные средние, найденные путём многократны прогонов модели на ЭВМ. Сходимость выборочных средних к средним значениям с ростом объема выборки называется стохастической. Эта сходимость, как правило, медленная. Если s - стандартное отклонение одного наблюдения, то стандартное отклонение среднего N наблюдений будет равно 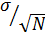 , т.е. для уменьшения ошибки случайной выборки в k раз требуется увеличить объем выборки в k2 раз.
, т.е. для уменьшения ошибки случайной выборки в k раз требуется увеличить объем выборки в k2 раз.
Медленная сходимость преодолевается применением ускоренных методов моделирования, обеспечивающих снижение дисперсии оценки (расслоенная выборка, взвешенная выборка и др.).
Выделяют этапы стратегического планирования:
1) построение структурной модели;
2) построение функциональной модели.
Структурная модель выбирается исходя из того, что должно быть сделано, характеризуется числом факторов и числом уровней для каждого фактора.
Число элементов эксперимента Nс = q1,q2…qk, где k – число факторов, 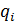 ,
, 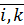 – число уровней i – фактора.
– число уровней i – фактора.
Элемент структурной модели – структурный блок эксперимента, определяемый как простейший эксперимент в случае одного фактора и одного уровня.
Необходимо выделять наиболее существенные факторы. Выделять уровни.Минимальноечисло уровней каждого фактора равно 2.
Анализ результатов существенно упрощается, если уровни равноотстоят друг от друга.
Аналитические упрощения. если 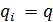 ,
, 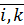 – симметричная структурная модель, т.е.
– симметричная структурная модель, т.е. 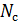 =
= 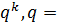
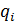 ,
, 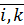 .
.
Функциональная модель ПЭ определяет количество элементов структурной модели, т.е. необходимое число различных информационных точек Nф.
Функциональная модель может быть полной (Nф=Nс) и неполной (Nф<Nс).
Основная цель построения функциональной модели – нахождение компромисса между необходимыми действиями и ограничением ресурсов.
Для анализа возможностей рассматривают попарно относительное влияние числа факторов. числа уровней и числа повторений на количество необходимых машинных прогонов N модели.
Пусть полное число прогонов при симметрично повторяемом эксперименте равно  n – необходимое число повторений эксперимента, q– число уровней каждого фактора, k– число факторов.
n – необходимое число повторений эксперимента, q– число уровней каждого фактора, k– число факторов.
Какая из трех величин дает наибольшее сокращение полного количества прогонов?
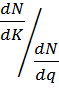 =
=  ;
; 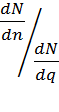 =
= 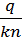 ;
; 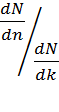 =
=  .
.
Анализ приведенных отношений показывает:
1) если kn > q и k > q ln q, то доминирует q;
2) если k < q ln q и n ln q > 1, то доминирует k;
3) если n ln q < 1 и q > kn, то доминирует n.
(доминирует – обеспечивает более крутую производную).
Таким образом. использование структурных и функциональных моделей позволяет рационально построить план эксперимента с учетом наличных ресурсов.
Тактическое планирование машинных экспериментов
Здесь решают проблемы:
- определения начальных условий и их влияния на достижения установившегося результата при моделировании; определяется влиянием переходного периода;
- обеспечения точности и достоверности результатов моделирования; реализуется через дисперсию оценки;
- уменьшения дисперсии оценок характеристик процесса функционирования моделируемых систем; реализуется через применение методов понижения дисперсии
- выбора правил автоматической остановки имитационного эксперимента с моделями; применение метода автоостонова.
|
|
|


