 |
Понятие предела функции в точке.
|
|
|
|
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ, ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
"ОМСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ"
ИНСТИТУТ ВЕТЕРИНАРНОЙ МЕДИЦИНЫ
_________________________________________________________________
ПРИХОДЬКО М.А., СЕЧКИНА И.В.
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ
РЕКОМЕНДОВАНО УЧЕНЫМ СОВЕТОМ ИВМ ОмГАУ
В КАЧЕСТВЕ УЧЕБНОГО ПОСОБИЯ
ОМСК - 2005
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ, ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
"ОМСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ"
ИНСТИТУТ ВЕТЕРИНАРНОЙ МЕДИЦИНЫ
_________________________________________________________________
ПРИХОДЬКО М.А., СЕЧКИНА И.В.
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ
РЕКОМЕНДОВАНО УЧЕНЫМ СОВЕТОМ ИВМ ОмГАУ
В КАЧЕСТВЕ УЧЕБНОГО ПОСОБИЯ
ОМСК - 2005
Оглавление.
Введение………………………………………………………………стр 3
§1 Введение в анализ……………………………………………..4
1.1.Понятие предела функции в точке…………………………………4
1.2. Бесконечно малые и бесконечно большие функции……………4
1.3. Основные теоремы о пределах…………………………………….6
1.4. Односторонние пределы……………………………………………10
1.5. Непрерывные функции…………………………………………….10
§ 2. Производная функция………………………………………17
2.1. Определение производной, её физический, геометрический смысл. …………………………………………………………………17
2.2. Правила дифференцирования. Таблица производных…………19
2.3. Производные высших порядков. …………………………………22
|
|
|
Дифференциал функции.
Геометрический смысл дифференциала. …………………………23
2.5. Вычисление пределов по правилу Лопиталя…………………….25
§3. Исследование функций при помощи производных…………………30
3.1. Монотонность функции……………………………………………..30
3.2. Экстремум функции………………………………………………….31
3.3. Направление выпуклости графика функции.Точки перегиба…32
3.4. Асимптоты графика функции………………………………………34
§ 4. Общая схема исследования функции…………………………………35
Типовой расчет №1………………………………………………………..42
Заключение…………………………………………………………………52
Литература………………………………………………………………….53
ВВЕДЕНИЕ
«Значением математики сейчас непрерывно возрастает. В математике рождаются новые идеи и методы. Все это расширяет сферу ее приложения. Сейчас уже нельзя назвать такой области деятельности людей, где математика не играла бы существенной роли. Она стала незаменимым орудием во всех науках о природе, в технике, в обществоведении. Даже юристы и историки берут на свое вооружение математические методы». В этих словах академика А.Д. Александрова ярко выражена мысль о значимости математики, о ее проникновении в другие науки.
Понятие функции является одним из основных общенаучных понятий, к нему приводит рассмотрение многих задач, поставленных в ряде естественных наук.
Дифференциальное исчисление является одним из аппаратов исследования функциональных зависимостей. Этот раздел является одним из фундаментальных в курсе дисциплины "Математика". Изучение данного раздела, как показала практика, вызывает определенные трудности. Помочь преодолеть их, по мнению авторов, призвано данное пособие.
Настоящее пособие соответствует государственному образовательному стандарту, программе дисциплины "Математика" для студентов специальности 310800 и представляет комплексное изложение теоретического материала, сопровождаемо многочисленными примерами, в том числе и прикладной направленности.
|
|
|
Весь материал разбит на четыре параграфа, в которых изложение теоретического материала ведется параллельно с иллюстрирующими его примерами. Изложение материала ведется на доступном, но достаточно строгом, языке. В конце каждого параграфа предложены задания для самостоятельной работы в объеме, достаточном как для аудиторной работы, так и для самостоятельной подготовки по указанным разделам. Для обеспечения самопроверки приведены ответы к большинству предложенных заданий.
Авторы выражают надежду на то, что данное пособие не только окажет практическую помощь в овладении знаниями и приобретении умений решать задачи по данной по теме, но и поможет читателю получить эстетическое наслаждение от общения с математикой, т.к. ряд ее особенностей (например, абстрактность, единство частей, совершенство языка) позволяют считать эту науку одним из источников эстетического воздействия.
«Оперирование с бесконечным может стать
надежным только через конечное».
(Д. Гильберт)
Введение в анализ.
Понятие предела функции в точке.
Пусть функция определена на некотором интервале, содержащем точку 
, кроме, быть может, самой точки .
Определение. Число А называется пределом функции 
в точке , если для любого 
(которое может быть сколь угодно малым) существует такое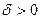 
, что для всех 
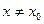, удовлетворяющих условию 
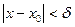имеет место неравенство 
.
Обозначение: 
.
На графике это можно изобразить следующим образом (рис.1):
Рис. 1
Выберем произвольно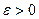 
и отложим его от точки А вверх и вниз, как на рисунке. Видно, что разность , если разность 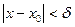. Из графика видно, что какое бы малое число 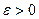мы не взяли, для него найдётся 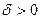(зависящее от ), такое, что разность , как только .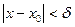
|
|
|
