 |
Задания для самостоятельной работы.
|
|
|
|
№1.Вычислить производные указанных функций, используя таблицу производных и правила дифференцирования:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  ;
;
6)  ;
;
7)  ;
;
8)  ;
;
9)  ;
;
10)  ;
;
11) 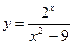 ;
;
12)  ;
;
13)  ;
;
14)  ;
;
15)  ;
;
16)  ;
;
№2. Привести несколько примеров функции  , для которой:
, для которой:
а) 
б) 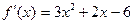 ;
;
№3.  . При каких значениях x выполняется условие:
. При каких значениях x выполняется условие:

№4. Вычислить  если
если  .
.
№5. Вычислить значения производной функции  в точках, в которых значение этой функции равно 0:
в точках, в которых значение этой функции равно 0:

№6. Тело движется по прямой так, что расстояние  от начальной точки изменяется по закону
от начальной точки изменяется по закону  (м), где
(м), где  - время движения в секундах. Через сколько секунд после начала движения тело остановится?
- время движения в секундах. Через сколько секунд после начала движения тело остановится?
№7. Материальная точка массой 2г движется прямолинейно по закону  (
( - в сантиметрах,
- в сантиметрах,  - в секундах). В момент времени
- в секундах). В момент времени  найдите:
найдите:
а) скорость 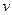 движения точки;
движения точки;
б) ускорение движения  ;
;
в) силу, действующую на точку  .
.
№8. Тело, выпущенное вверх с начальной скоростью  м/с, движется по закону
м/с, движется по закону  (
( - в метрах,
- в метрах,  - в секундах). Найдите момент времени, когда скорость движения тела будет в три раза меньше начальной скорости, считая что
- в секундах). Найдите момент времени, когда скорость движения тела будет в три раза меньше начальной скорости, считая что  м/с.
м/с.
№9. Показать, что функция  обращает уравнение
обращает уравнение  в тождество.
в тождество.
№10. Показать, что функция  удовлетворяет уравнению
удовлетворяет уравнению  .
.
№11. Показать, что функция  удовлетворяет уравнению
удовлетворяет уравнению  .
.
№12. Найти дифференциал функции  в точке
в точке  , если
, если  ,
,  .
.
№13. Найти производные второго порядка от следующих функций:

№14. Применяя правило Лопиталя вычислить пределы функций:
1) 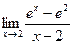 ; 2)
; 2)  ;
;
3)  4)
4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8) 
Ответы:
№1.1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  ; 10)
; 10)  ; 11)
; 11) 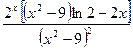 ; 12)
; 12) 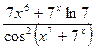 ; 13)
; 13)  ; 14)
; 14)  ; 15)
; 15)  ; 16)
; 16)  .
.
№3. а)1; -2; б) 0; -1;
№4.  ;
;
№5. а)  ; б) 2;
; б) 2;
№6. 2 с;
№7. а) 25 см/с; б) 16 см/с 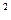 ; в) 32 дины.
; в) 32 дины.
№8. 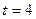 с.
с.
№12.  ;
;
№13. 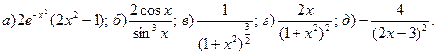
№14. 
«Я с дрожью ужаса отворачиваюсь от ваших несчастных
проклятых функций, у которых нет производных».
|
|
|
(Ш. Эрмит)
Исследование функций при помощи производных.
Возможность применения производных для исследования функций основана на зависимости, существующей между производными и особенностями графика функции.
Монотонность функции.
Теорема. Пусть функция  непрерывна на
непрерывна на  и дифференцируема на
и дифференцируема на  .
.
1. Если  для любого значения аргумента
для любого значения аргумента  из интервала
из интервала  , то функция
, то функция  возрастает на этом интервале.
возрастает на этом интервале.
2. Если  для любого значения аргумента
для любого значения аргумента  из интервала
из интервала  , то функция
, то функция  убывает на этом интервале.
убывает на этом интервале.
3.  Если
Если  для любого значения аргумента
для любого значения аргумента  из интервала
из интервала  , то функция
, то функция  постоянна на этом интервале.
постоянна на этом интервале.
Пример: Определить интервалы монотонности заданной функции.
1) 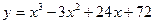 .
.
Решение. Функция определена, непрерывна и дифференцируема на всей числовой оси. Найдем производную первого порядка функции.  .
.
Корни производной найдем из условия  .
.

Методом интервалов исследуем знаки первой производной (рис.9).

Рис.9
При  или
или  производная
производная  , следовательно, функция возрастает. Для
, следовательно, функция возрастает. Для  производная
производная 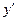 <0, следовательно, функция убывает.
<0, следовательно, функция убывает.
2)  .
.
Решение. Функция определена, непрерывна и дифференцируема на всей числовой оси.


Рис.10
Функция возрастает, если 
Функция убывает, если  (рис.10).
(рис.10).
Экстремум функции.
Теорема (I достаточное условие существования экстремума функции).
Если производная функции  в точке
в точке  равна 0 (
равна 0 ( ) и при переходе через эту точку изменяет знак на противоположный, то данная точка
) и при переходе через эту точку изменяет знак на противоположный, то данная точка  является точкой экстремума функции, а именно:
является точкой экстремума функции, а именно:
- точкой максимума, если при переходе через неё слева направо знак производной изменяется с + на -.
- Точкой минимума, если при переходе через неё слева направо знак производной изменяется с - на +.
Для определения точек экстремума можно воспользоваться также следующей теоремой.
Теорема (II достаточное условие существования экстремума).
Пусть  и
и  , тогда
, тогда  - точка экстремума функции
- точка экстремума функции  , причем
, причем  -точка максимума, если
-точка максимума, если  ,
,
|
|
|
 - точка минимума, если
- точка минимума, если 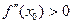 .
.
Экстремумом функции называют значение функции в точке экстремума.
Пример. Найти экстремумы функции  .
.
Решение. Функция определена, непрерывна и дифференцируема при  .
.
 .
.
Для нахождения точек экстремума воспользуемся I достаточным признаком.


Рис.11
x =0 - точка max, т.к. знак производной изменяется с + на -.
x =6 - точка min, т.к. знак производной изменяется с - на +.

Значения 0 и 12 - экстремумы функции (рис.11).
|
|
|


