 |
Производные высших порядков.
|
|
|
|
Производную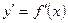 
функции 
называют также производной первого порядка. Функция 
также может быть дифференцируемой, ее производная будет называться производной второго порядка функции .
Обозначение: 
, 
.
Производная от производной второго порядка (если она существует) называется производной третьего порядка и т. д.
Производной 
- го порядка называется производная от производной 
- го порядка, т. е. 
.
Для обозначения производных четвертого и выше порядков используют римские цифры. Например, 
или 
- производная шестого порядка. Производные порядков, выше первого, называются производными высших порядков.
Пример 1. Вычислить производную третьего порядка функции 
.
Решение: Нахождение производной третьего порядка необходимо начать с производной первого порядка.
.
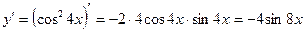
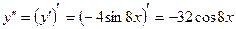
Если функция описывает закон прямолинейного движения материальной точки, то производная второго порядка функции представляет собой скорость изменения скорости функции (т. е. ускорение) в определенный момент времени 
. В этом состоит ее физический смысл.
Пример 2. Найти зависимость ускорения прямолинейного движения, заданного законом от времени 
.
Решение:
.
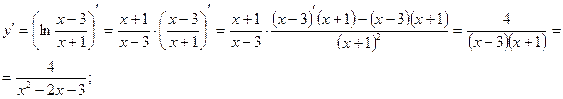
Пример 3. Точка движется прямолинейно по закону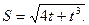 
Найти скорость и ускорение движения точки для момента времени t=1 (S дается в сантиметрах,t -в секундах).
Решение: скорость 
;
ускорение 
Следовательно, в момент времени t = 1: 
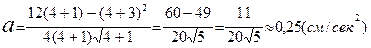
Дифференциал функции. Геометрический смысл дифференциала.
С понятиями производной тесно связано понятие дифференциала (от него происходит название дифференциального исчисления). Пусть функция определена в некоторой окрестности точки 
. Дадим аргументу приращение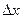 
и рассмотрим приращение функции 
.
|
|
|
Определение. Функция называется дифференцируемой в точке , если приращение функции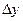 
в точке может быть представлено в виде 
, где 
и 
- бесконечно малые при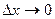 
, причем 
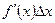- бесконечно малая величина одного порядка с 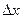( - бесконечно малая функция более высокого порядка, чем 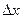). Величина 
называется главной частью приращения функции или дифференциалом функции в точке и обозначаемая 
.
Определение. Дифференциалом функции в точке называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, т. е. 
ил 
.
Примеры.
1). Найти дифференциал функции 
.
Решение.По формуле 
находим 
.
2).Найти дифференциал функции 
в точке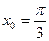 
, если 
.
Решение: 
.
.
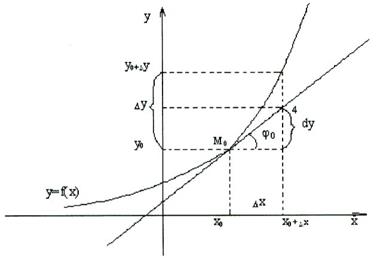
Геометрический смысл дифференциала:
L
K
Рис. 8
Проведем к графику функции в точке 
касательную 
, угол наклона которой равен 
. Рассмотрим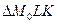 
, в котором сторона 
. Учитывая, что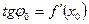 
, 
, получим: 
, сравнивая с определением дифференциала функции.
.
Т.о. дифференциал функции в точке равен приращению ординаты касательной, проведенной к графику функции в этой точке, когда аргумент получит приращение 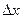(рис.8). Из определения дифференциала и правил вычисления производных следуют правила вычисления дифференциала функции:
1. 
;
2. 
;
3. 
;
4. 
;
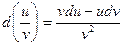Вычисление пределов по правилу Лопиталя.
(Гильом Франсуа Антуан де Лопиталь (1661-1704), французский математик; автор первого учебника по дифференциальному исчислению).
Пусть функци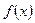и 
и 
дифференцируемы в некоторой окрестности точки , за исключением, быть может, самой точки и 
. Пусть также 
(или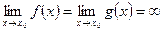 
) в указанной окрестности точки . Тогда, если существует 
, то 
.
Правило применимо для устранения неопределенностей 
и других неопределенностей, к ним сводящихся.
Если в частном 
в точке 
неопределенность 
или 
по прежнему остается, то следует перейти к отношению 
и т. д..
Примеры. Вычислить пределы, используя правило Лопиталя.
|
|
|
|
|
|
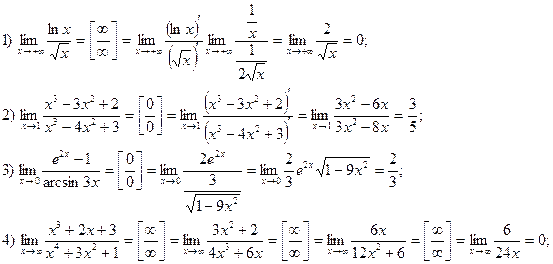
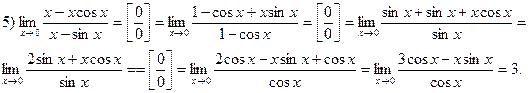
