 |
Раскрытие математических неопределённостей.
|
|
|
|
I. При вычислении  возможен случай, когда
возможен случай, когда  =0, т.е. дробь терпит разрыв в точке
=0, т.е. дробь терпит разрыв в точке  . В этом случае говорят, что имеем неопределённость
. В этом случае говорят, что имеем неопределённость  . Происходит это потому, что функции
. Происходит это потому, что функции  содержат множитель
содержат множитель  , который обращается в 0 при
, который обращается в 0 при  .Необходимо его выделить и сократить дробь по схеме:
.Необходимо его выделить и сократить дробь по схеме: 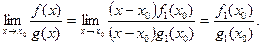
Примеры. Найти указанные пределы:

Решение. 1) Найдём корни трёхчленов: 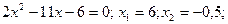
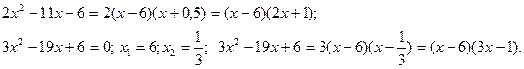
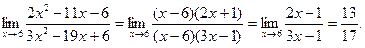
2) Умножим числитель и знаменатель дроби на сопряженные им выражения

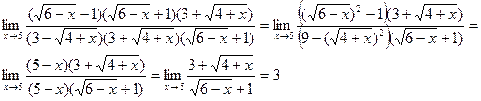
3) Во многих случаях используют первый замечательный предел и следствия из него:  .
.
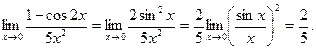
II. Если при  и
и  , то отношение
, то отношение  представляет неопределённость вида
представляет неопределённость вида  . В этом случае рекомендуется числитель и знаменатель дроби разделить на старшую степень x.
. В этом случае рекомендуется числитель и знаменатель дроби разделить на старшую степень x.
Примеры. Вычислить указанные пределы:

Решение. 1) Разделив числитель и знаменатель дроби на старшую степень  , получим:
, получим:
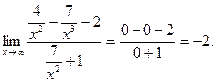
2) Старшая степень в этом примере  , поэтому числитель и знаменатель разделим на x:
, поэтому числитель и знаменатель разделим на x: 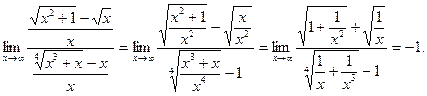
III. При вычислении  возможен случай, когда
возможен случай, когда  и
и  . Тогда разность
. Тогда разность  есть неопределённость
есть неопределённость  . С помощью тождественных преобразований она приводится к виду
. С помощью тождественных преобразований она приводится к виду  или
или  .
.
Пример. Вычислить предел 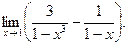
Решение. Приведём дроби к общему знаменателю, предварительно разложив знаменатель первой дроби по формуле разности кубов. 
IV.Раскрытие степенных неопределённостей 
Пусть необходимо найти  .
.
Если при этом:
 и
и  , то имеем неопределённость
, то имеем неопределённость  ;
;
 и
и  , то имеем неопределённость
, то имеем неопределённость 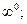
 и
и  , то имеем неопределённость
, то имеем неопределённость  .
.
Эти неопределённости раскрываются с помощью второго замечательного предела: 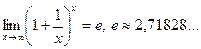
Используются также следствия из этой формулы:
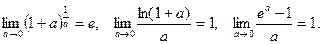
Примеры. Вычислить указанные пределы:
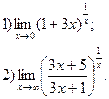
Решение.
1) 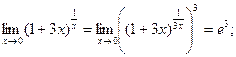
2) Здесь  , поэтому получим неопределённость вида
, поэтому получим неопределённость вида  . Так как
. Так как  , то
, то  . Обозначим
. Обозначим  , тогда
, тогда 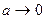 при
при  , причём
, причём  . Найдём предел основания:
. Найдём предел основания:  . Найдём предел показателя:
. Найдём предел показателя:  .Таким образом
.Таким образом  .
.
|
|
|
Односторонние пределы.
Если  и
и  , то принято писать
, то принято писать  . Если
. Если  и
и  , то принято писать
, то принято писать  . Пределы
. Пределы  и
и 
 , если они существуют, называют соответственно пределом слева (левосторонним пределом) функции
, если они существуют, называют соответственно пределом слева (левосторонним пределом) функции  в точке
в точке  и пределом справа (правосторонним пределом) функции
и пределом справа (правосторонним пределом) функции  в точке
в точке  . Для существования предела функции
. Для существования предела функции  в точке
в точке  необходимо и достаточно, чтобы односторонние пределы существовали порознь и равнялись бы между собой, т.е.
необходимо и достаточно, чтобы односторонние пределы существовали порознь и равнялись бы между собой, т.е.  .
.
Примеры. Найти односторонние пределы функции:
1)  при
при  ;
;
2)  при
при  ;
;
Решение. 1)  , т. к.
, т. к.  .
.
 , т. к.
, т. к.  .
.
Пределы оказались неравными, следовательно, предела функции в точке  не существует.
не существует.
2)  , где
, где  ; отсюда видно, что если
; отсюда видно, что если  , то
, то  .
.
 .
.
Пределы оказались неравными, следовательно, предела функции в точке 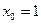 не существует.
не существует.
Непрерывные функции.
Для существования предела  не имеет значения, определяется или нет эта функция в точке
не имеет значения, определяется или нет эта функция в точке  . Например, функция
. Например, функция  не определена при
не определена при  (неопределенность
(неопределенность  ), однако
), однако  (первый замечательный предел).
(первый замечательный предел).
Дадим несколько определений непрерывной в точке  функции, если
функции, если  определена на некотором интервале, содержащем точку
определена на некотором интервале, содержащем точку  .
.
Определение. Функция  называется непрерывной в точке
называется непрерывной в точке  , если выполняется одно из следующих эквивалентных между собой условий:
, если выполняется одно из следующих эквивалентных между собой условий:
1.  (на языке пределов);
(на языке пределов);
2. Для всякой последовательности значений аргумента  , сходящейся к точке
, сходящейся к точке  , соответствующая последовательность
, соответствующая последовательность 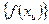 значений функции сходится к
значений функции сходится к  , то есть
, то есть 
 . (на языке последовательностей);
. (на языке последовательностей);
3.  ;
;
4. а) если 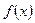 определена в точке
определена в точке  и вблизи этой точки;
и вблизи этой точки;
б) существует  , существует
, существует  и
и  ;
;
в)  .
.
Если нарушается хотя бы одно из условий а)- в) пункта 4, то в точке  функция терпит разрыв. При этом
функция терпит разрыв. При этом  - точка разрыва первого рода (точка конечного скачка), если существуют оба односторонних предела
- точка разрыва первого рода (точка конечного скачка), если существуют оба односторонних предела  и
и  ;
;  - точка разрыва второго рода (точка бесконечного скачка), если
- точка разрыва второго рода (точка бесконечного скачка), если  или
или  . На графике это выглядит следующим образом.
. На графике это выглядит следующим образом.







|

 y y y
y y y|
|
|
 | |||
 | |||




 x x
x x
x
(а) (б) (в)
Рис. 3
На рисунке 3 (а) график функции состоит из двух ветвей и одной точки  , где
, где  по условию:
по условию: 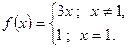
Функция определена на всей числовой прямой, неэлементарная, т. к. задана двумя различными формулами. Исследуем ее непрерывность в точке  , где изменяется ее аналитическое выражение:
, где изменяется ее аналитическое выражение:  . В точке
. В точке  устранимый разрыв, в остальных точках она непрерывна.
устранимый разрыв, в остальных точках она непрерывна.
На рисунке 3 (б) изображена функция  , она исследуется в точке
, она исследуется в точке  , в остальных точках данная функция определена. Найдем предел функции слева в точке
, в остальных точках данная функция определена. Найдем предел функции слева в точке  :
:  . Найдем предел справа в этой же точке:
. Найдем предел справа в этой же точке:  . Отсюда
. Отсюда  . Следовательно, в точке
. Следовательно, в точке  функция
функция  имеет разрыв первого рода. Скачок функции в точке
имеет разрыв первого рода. Скачок функции в точке  равен модулю разности
равен модулю разности  . Во всех других точках числовой прямой функция
. Во всех других точках числовой прямой функция  непрерывна, т. к. задана элементарными функциями.
непрерывна, т. к. задана элементарными функциями.
На рисунке 3 (в) представлена неэлементарная функция  , которая определена на всем множестве действительных чисел, задана тремя разными формулами на различных промежутках изменения аргумента:
, которая определена на всем множестве действительных чисел, задана тремя разными формулами на различных промежутках изменения аргумента: 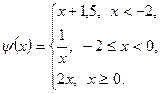
Исследуем непрерывность функции в точках  и
и  :
:  ;
;  .
.
По условию  , следовательно,
, следовательно,  , т. е.
, т. е.  непрерывна в точке
непрерывна в точке  .
.
 , т. е.
, т. е. 
 имеет разрыв второго рода. В остальных точках числовой оси функция непрерывна.
имеет разрыв второго рода. В остальных точках числовой оси функция непрерывна.
При отыскании точек разрыва функции следует учесть, что элементарная функция может иметь разрыв только в той точке, где она не определена.
Неэлементарная функция может иметь разрывы как в точках, в которых она не определена, так и в точках, где она определена; если функция задана несколькими различными аналитическими выражениями(формулами) для различных интервалов изменения аргумента, то она может иметь разрывы в тех точках, при переходе через которые изменяется ее аналитическое выражение.
|
|
|



